第一节 函数

「反函数」什么是反函数？

1. 比如 $y=x^3$ 的反函数就是 $x=\sqrt[3]{y}$
2. 函数与反函数之间关于 $y=x$ 对称

「反函数」反函数的性质

性质	原因
不是每个函数都有反函数（ $y=x^3$ 有，$y=x^2$ 没有）	原因：在函数的严格定义下，一个 𝑥 不能对应多个 𝑦。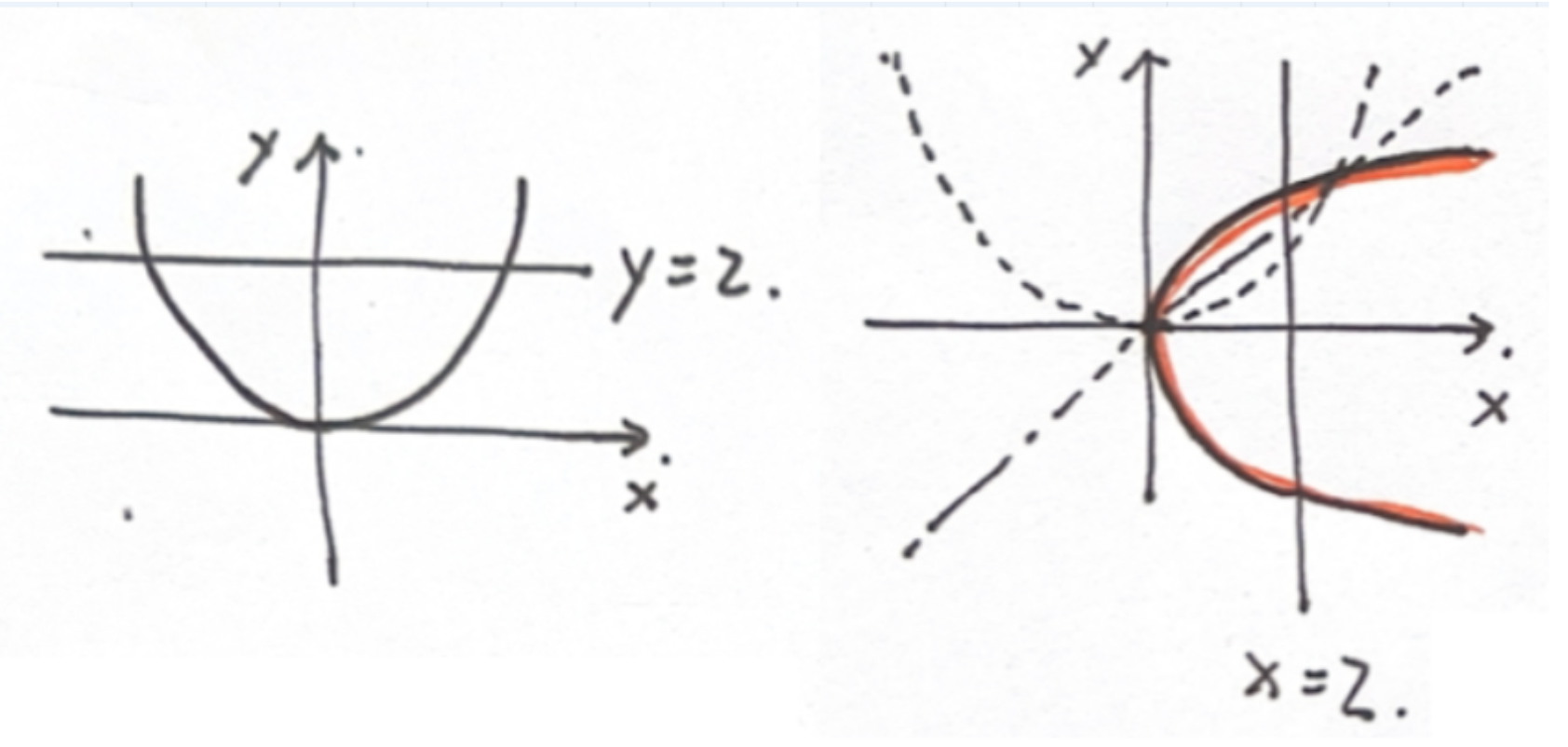
单调函数一定有反函数，反之不一定
在同直接坐标系下，$x$ 与 $y$ 可互换，即反函数是关于$y=x$对称的	$x=f^{-1}(y)\iff y=f^{-1}(x)$
反函数的反函数是原函数	$f^{-1}[f(x)]=x$ ，$f[f^{-1}(x)]=x$

求解复杂函数的反函数

「绝对值函数」绝对值函数

「符号函数」符号函数

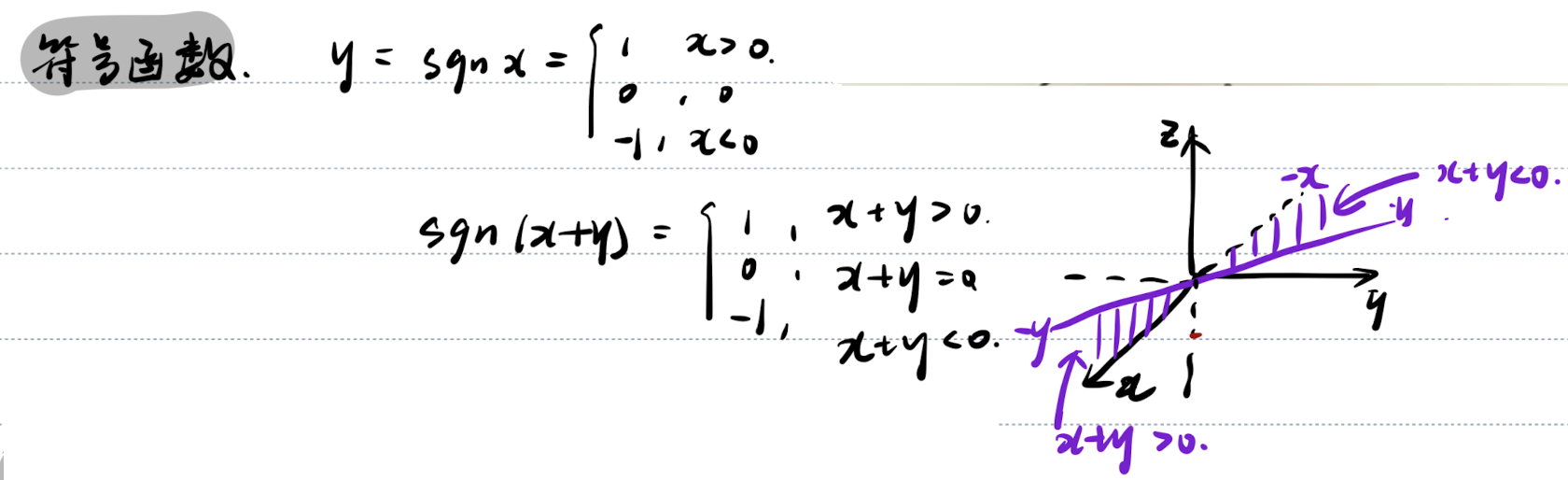
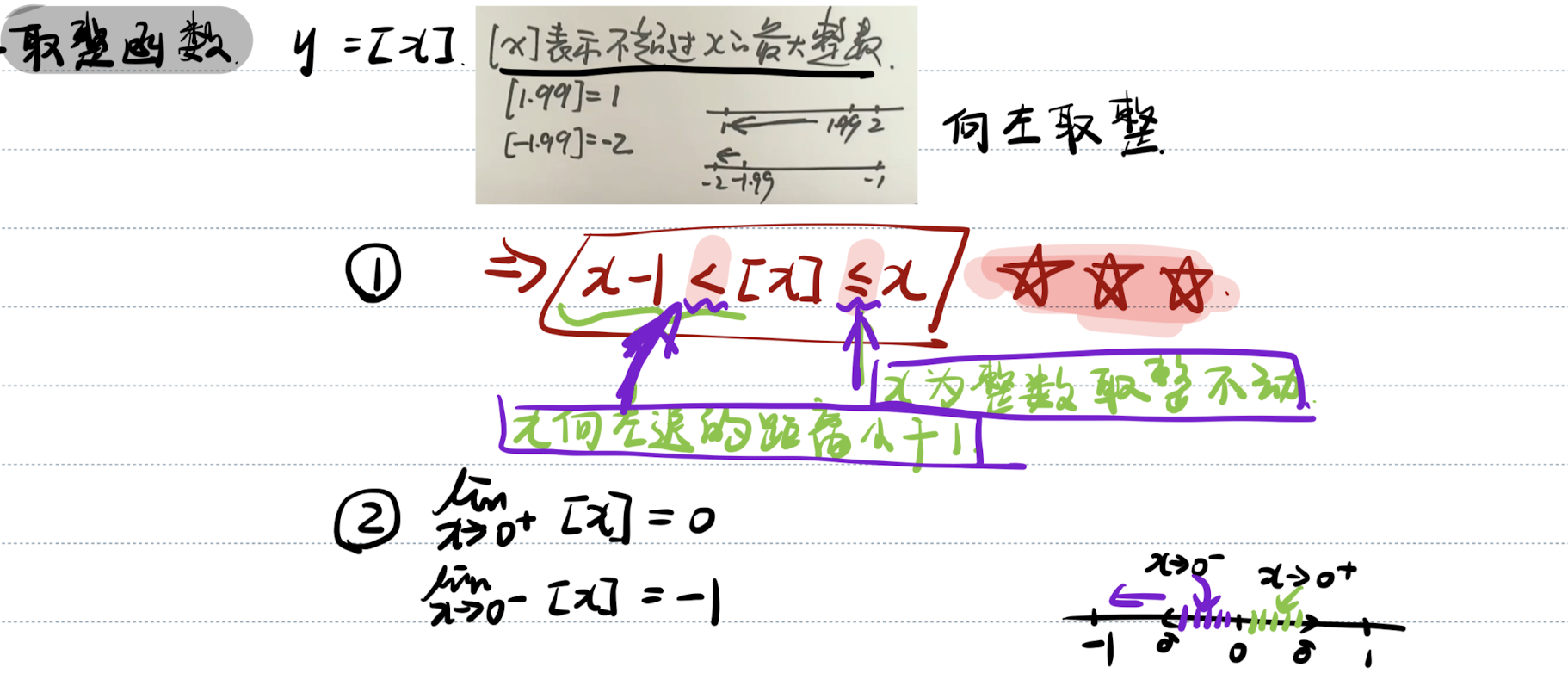
「取整函数」取整函数

「函数性质」伸缩变换

伸缩变换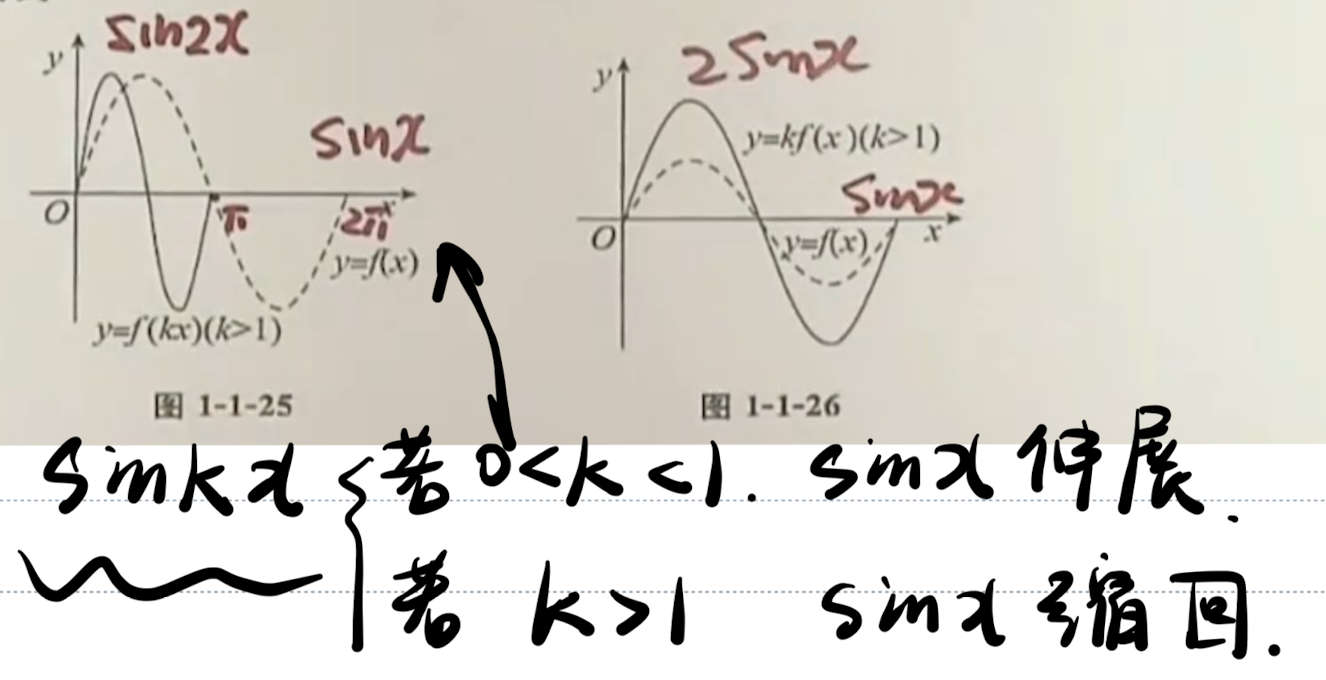

「初等函数」什么是初等函数？

初等函数定义
基本初等函数	幂函数 $y=x^{\mu }(\mu \mathrm{为}\mathrm{实}\mathrm{数})$ 指数函数 $y=a^x(a>0,a\ne 1)$ 对数函数 $y=lo{g}_{a}x(a>0,a\ne 1)$ 三角函数 $y=sinx,cosx,tanx,cotx,secx,cscx$ 反三角函数 $y=arcsinx,arccosx,arctanx$
初等函数	常数 + 基本初等函数 + 有限次四则运算 + 有限次函数的复合

「函数性质」单调性

函数的增减	$f(x)$	$f^{\prime }(x)$
单调增	$x_1<x_2\Rightarrow f(x_1)<f(x_2)$	$f^{\prime }(x)>0$
单调不减	$x_1\le x_2\Rightarrow f(x_1)\le f(x_2)$	$f^{\prime }(x)\ge 0$

「函数性质」奇偶性

奇偶性	特性	函数
偶函数	$f(-x)=f(x)$	$x^2,|x|,cosx,f(x)+f(-x),ln\frac{1-x}{1+x},ln(x+\sqrt{1+x^2}),\frac{e^x-1}{e^x+1},f(x)-f(-x)$
奇函数	$f(-x)=-f(x)$	$sinx,tanx,arcsinx,arctanx$ $f(x)$ 关于原点对称，若 $f(x)$ 在 $x=0$ 处有定义，则 $f(0)=0$
奇偶函数之间的关系	$\mathrm{奇}\times \mathrm{奇}=\mathrm{偶}$ $\mathrm{奇}\times \mathrm{偶}=\mathrm{奇}$ $\mathrm{偶}\times \mathrm{偶}=\mathrm{偶}$

$y=f(x)$关于 $x-T\ne 0$ 对称的充要条件

• $f(x)=f(2T-x)/f(x+T)=f(T-x)$

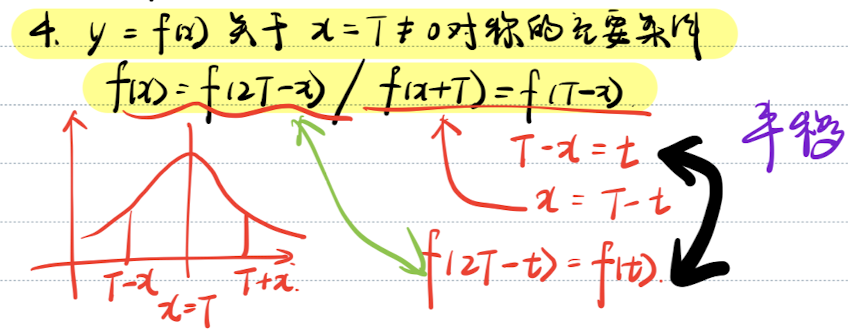
「函数性质」周期性

周期性
定义	$f(x+T)=f(x)$
特性	若 $f(x)$ 以 $T$ 为周期，$f(ax+b)$ 以 ${\displaystyle \frac{T}{|a|}}$ 为周期 + $\sin x、\cos x$ 以 $2\pi$ 为周期 + $\sin 2x、\tan x、\cot x$ 以 $\pi$ 为周期

「函数性质」有界性

有界性
定义	$y=f(x)$ 在集合 $X$ 上有定义 若存在 $M>0$，使得任意 $x\in X$，恒有 $|f(x)|\le M$，称 $f(x)$ 在 $X$ 上为有界函数，否则为无界函数
无界函数	$f(x)=x\sin x$ 为无界函数

• 简单上讲，如果函数能被区间端点所在垂直于x轴的直线包裹起来，则为有界
• 有界、无界的讨论首先要指明区间

连续与有界性的关系

• 连续可推有界

「重要结论」四特性