第三章 二维随机变量及其分布

第一节 联合分布函数

「联合分布」二维随机变量 定义

• 设 $X=X(\omega ),Y=Y(\omega )$ 为样本空间 $\mathrm{\Omega }$ 上的两个随机变量，称 $(X,Y)$ 为二维随机变量。

「联合分布」联合分布函数 定义

• 设 $(X,Y)$ 为二维随机变量，对任意实数 $x,y$，称 $F(x,y)=P\{X\le X,Y\le y\}$ 称为 $(X,Y)$ 的联合分布函数，简称分布函数。

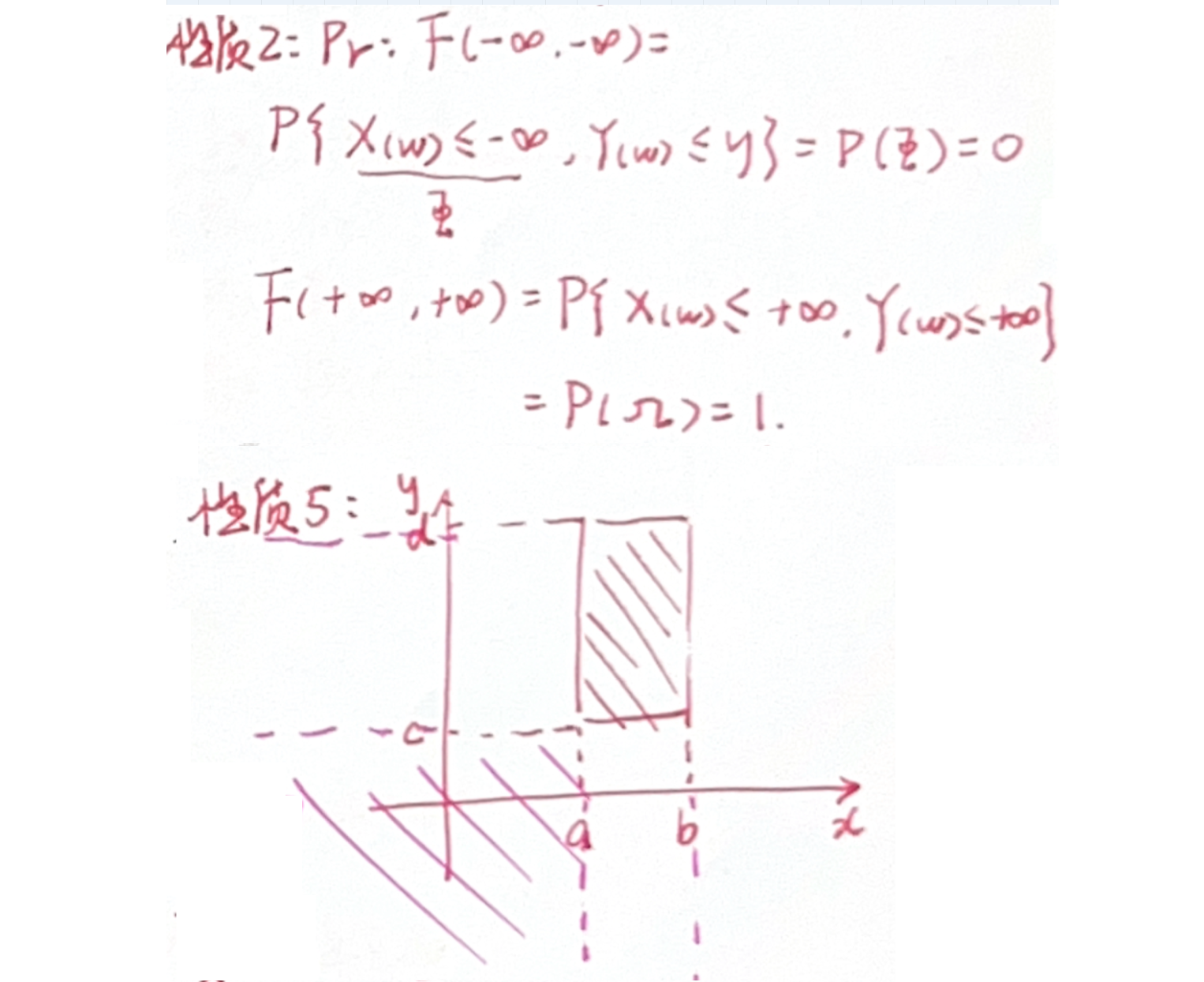
「联合分布」联合分布函数 性质

备注 & 证明

• 五个性质构成充要条件

「联合分布」边缘分布函数 定义

第二节 二维离散型随机变量

「二维离散」联合概率分布 定义

• 设二维随机变量 $(X,Y)$ 的取值有限个或可列个，称 $(X,Y)$ 为二维离散型随机变量
• 设 $(X,Y)$ 的取值为 $(x_i,y_i),i,j=1,2,\cdots$，称 $P\{X=x_i,Y=y\}=p_{ij},i,j=1,2,\cdots$ 为 $(X,Y)$ 的联合概率分布，简称概率分布，也可用列表法表示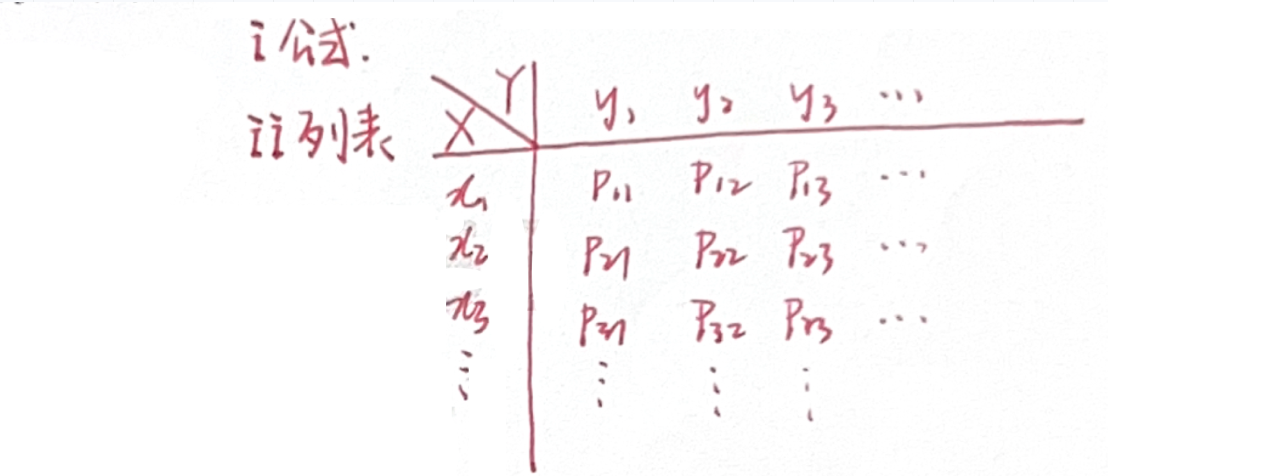

「二维离散」联合概率分布 性质

「二维离散」边缘概率分布 定义

「二维离散」条件概率分布 定义

第三节 二维连续性随机变量

「二维连续」联合概率密度 定义

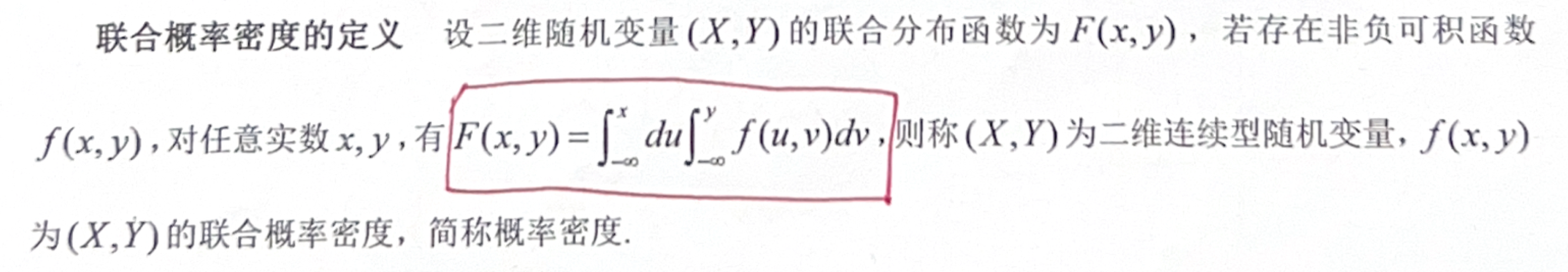
「评注」

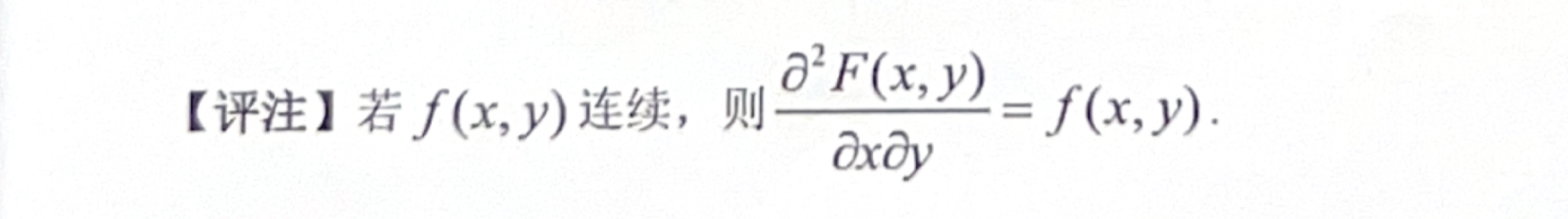
「二维连续」联合概率密度 性质

「评注」

• 性质 (1)(2) 是判定概率密度的充要条件
• 性质 (3) 用于计算随机变量取值的概率

「二维连续」边缘概率密度 定义

「二维连续」条件概率密度 定义

第四节 随机变量的独立性

「随机变量」相互独立的定义

• 设二维随机变量 $(X,Y)$ 的联合分布函数为 $F(x,y)$ ，边缘分布函数分别为$F_X(x)$ 和 $F_Y(y)$ 。 若对任意实数 $x,y$，有 $F(x,y)=F_X(x)F_Y(y)$，则称随机变量 $X$ 与 $Y$ 相互独立（互不影响）。

「随机变量」相互独立的充要条件

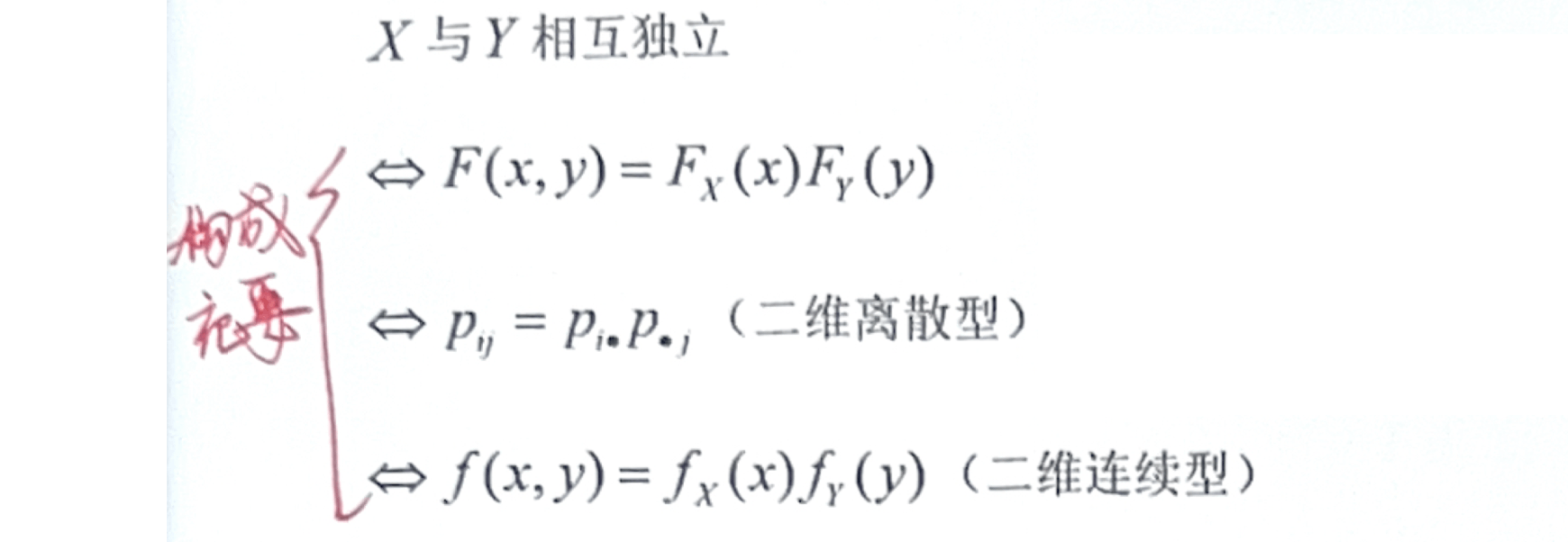
证明

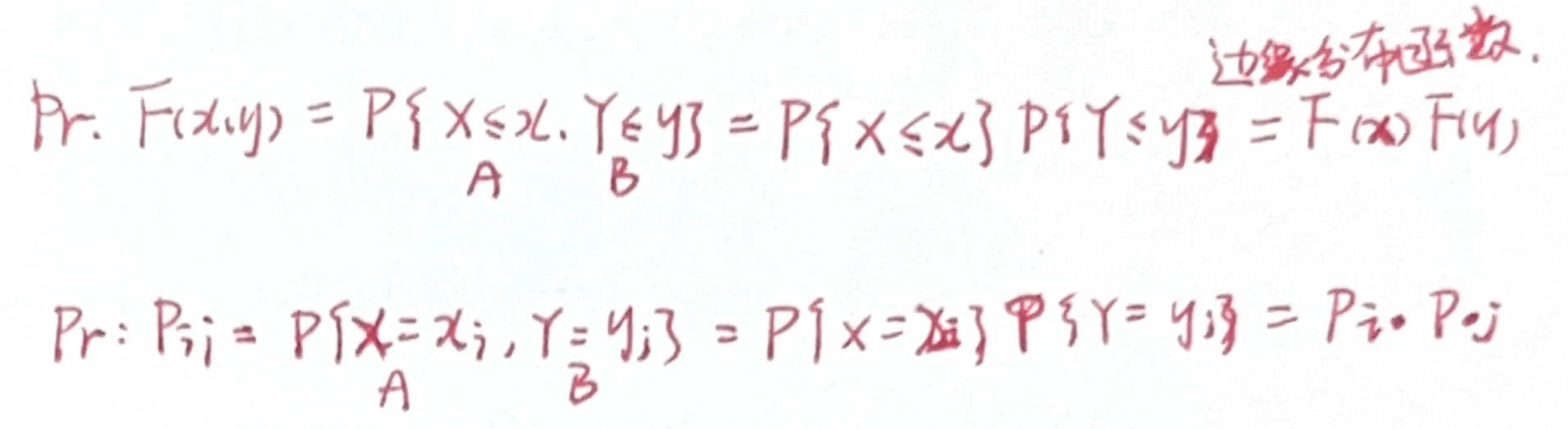
「评注」

若 $X$ 与 $Y$ 相互独立，$h,g$为连续函数，则 $h(X)$ 与 $g(Y)$ 相互独立，即相互独立的随机变量的函数仍然相互独立

第五节 二维均匀分布与二维正态分布

「二维均匀分布」定义

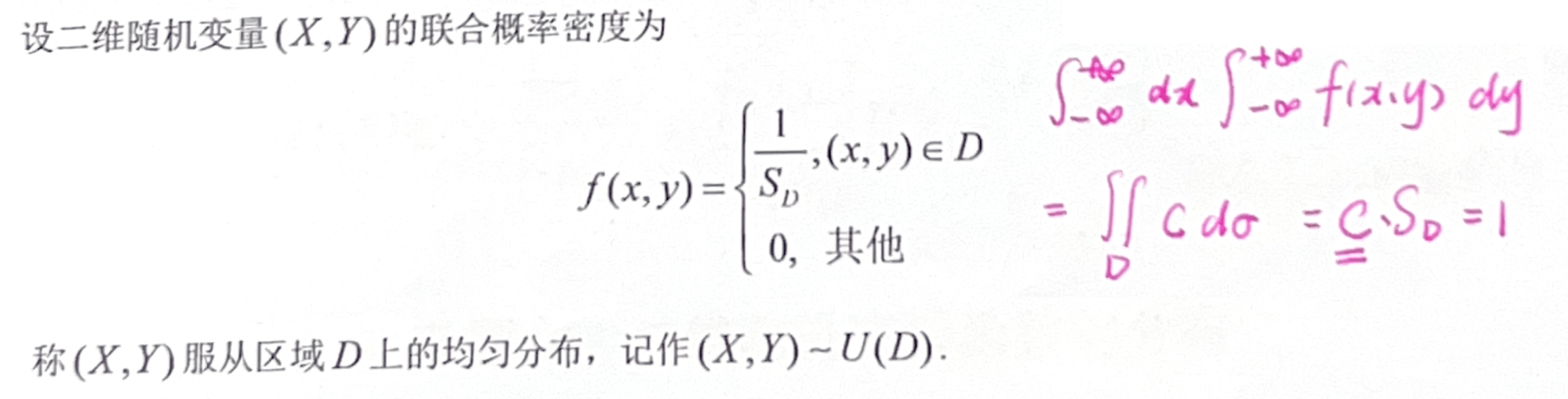
「二维均匀分布」性质

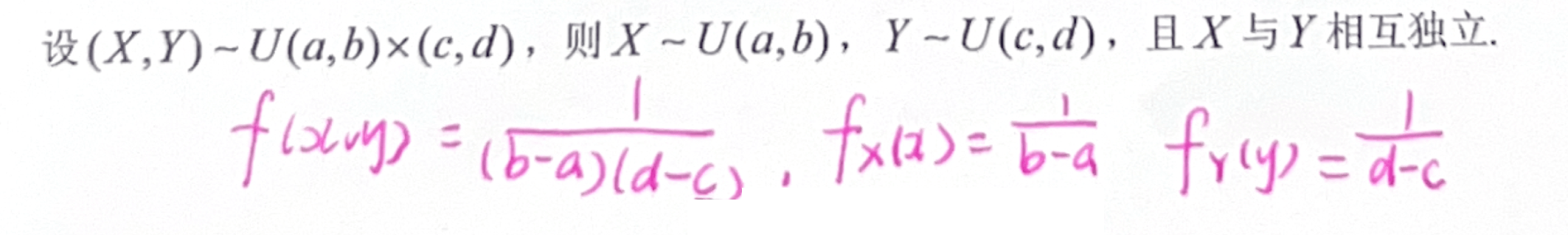
「二维正态分布」定义

「二维正态分布」性质

第六节 二维随机变量函数的分布

「随机变量函数分布」二维离散

「随机变量函数分布」二维连续

• 设二维随机变量 $(X,Y)$ 的联合概率密度 $(x,y)$，求 $Z=g(X,Y)$ 的概率密度.

分布函数法

卷积公式

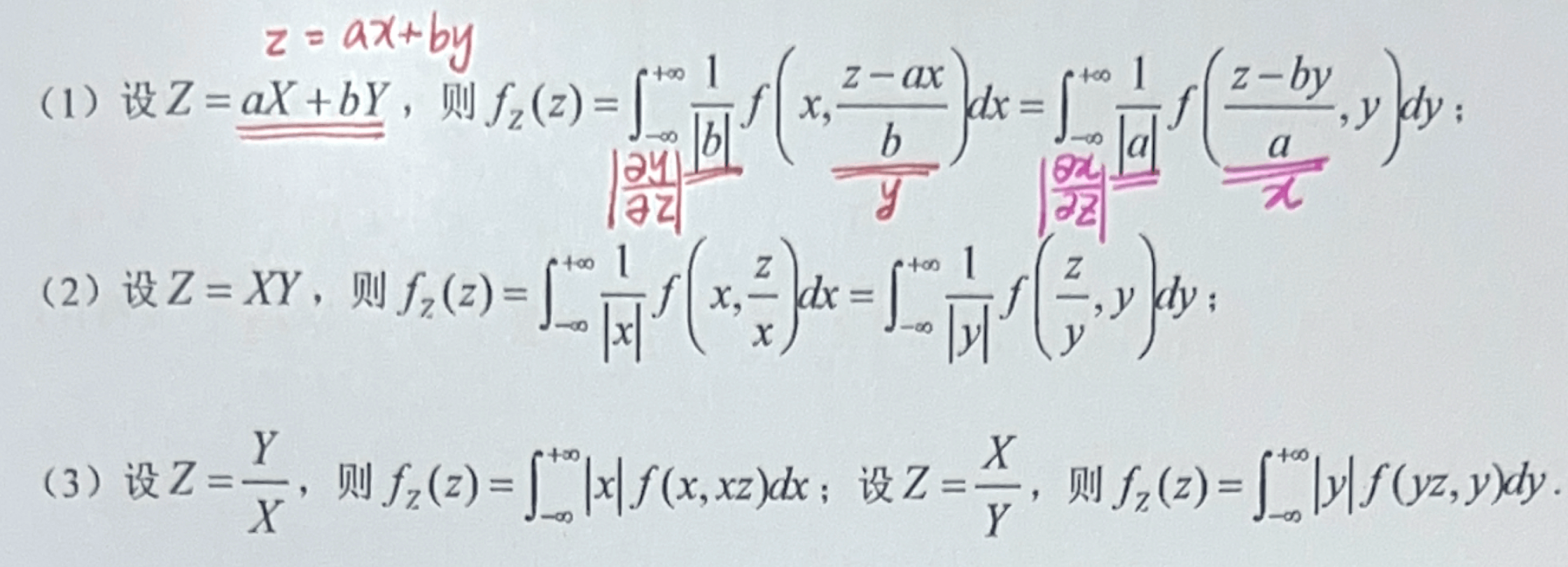
「随机变量函数分布」一离散一连续

• 已知离散型随机变量 $X$ 的概率分布与连续型随机变量 $Y$ 的概率密度，求$Z=g(X,Y)$ 的分布
• 利用分布函数法，由全概率公式，对 $X$ 的所有取值展开计算。

「最值函数」最值函数的分布