第五章 特征值与特征向量

第一节 特征值与特征向量的概念

「特征值与特征向量」定义

评注

1. 设 $A$ 为 $n$ 阶矩阵，$\alpha$ 为线性方程组 $Ax=0$ 的非零解，则 $\alpha$ 为矩阵 $A$ 属于特征值 $0$ 的特征向量。 $Pr:A\alpha =0=0\cdot \alpha (\alpha \ne 0)$
2. 设 $n$ 阶矩阵 $A$ 的各行元素之和均为 $\lambda$，则 $(1,1,\cdots ,1{)}^T$ 为矩阵 $A$ 属于特征值 $\lambda$ 的特征向量。

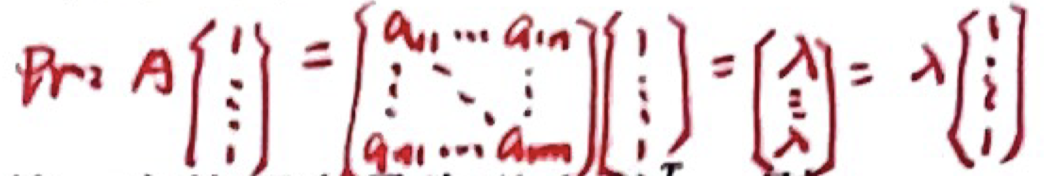
「特征多项式与特征方程」定义

「特征方程」特征方程法

「特征值与特征向量」性质

「特征值与特征向量」求法

1. A 为数字矩阵：特征方程法
2. A 为抽象矩阵：利用特征值与特征向量的定义或性质

第二节 相似矩阵

「相似矩阵」定义

• 设 $A、B$ 为 $n$ 阶矩阵，若存在 $n$ 阶可逆矩阵 $P$，使得$B=P^{-1}AP$，则称A与B相似，记作 $A\sim B$.

「相似矩阵」性质

第三节 相似对角化

「评注」

• 若 $A、B$ 均可相似对角化，则 $A$ 与 $B$ 相似 $\iff$ $A,B$有相同的特征值

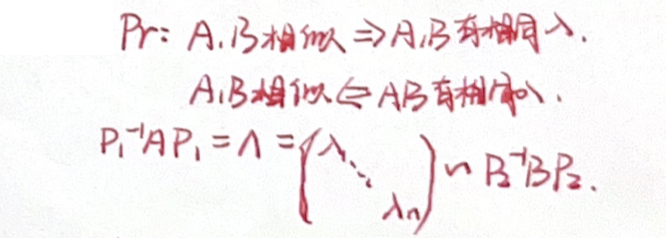
「相似对角化」充分条件