第十三节 常微分方程
「概念」微分方程
| 微分方程 | |
|---|---|
| 定义 | 含有未知函数的导数或微分的方程 |
| 阶 | 未知函数最高阶导数的阶数 |
| 解 | 满足微分方程的函数 |
| 通解 | 微分方程的解中独立常数的个数等于微分方程的阶数,称为通解。 常数 |
| 特解 | 不含任意常数的解 |
| 初始条件 | 确定通解中常数(特解)的条件。 确定了通解的常数后,通解就变成了特解 |
| 积分曲线 | 方程的一个解在平面上对应一条曲线 |
「一阶」 变量可分离型
- 把
与 放在一起, 和 放在一起,求解方法是两端积分。
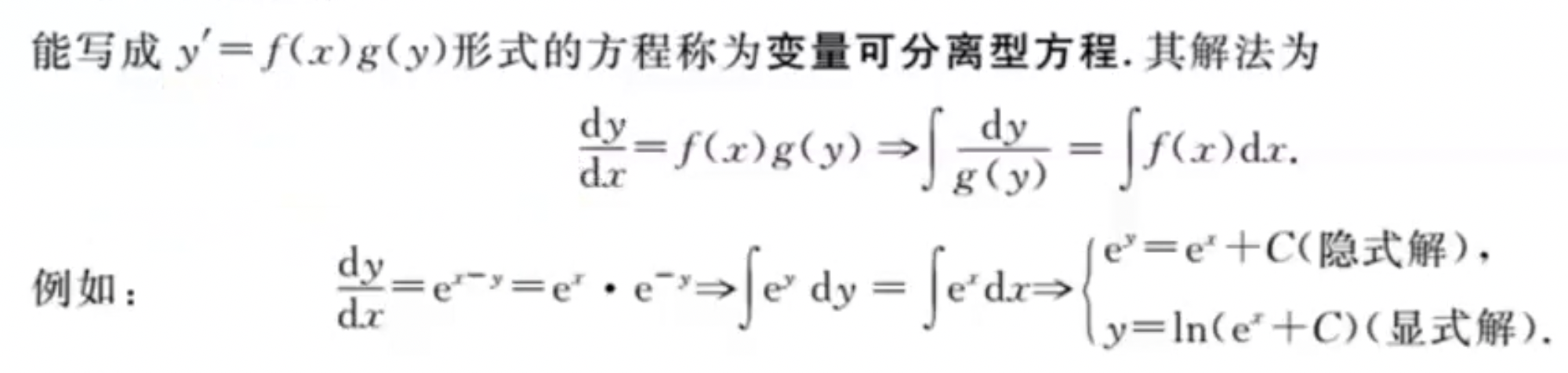
变量可分离型方程 举例
- 在解微分方程的时候,可能会丢掉一些解,比如这题中的
,这些丢掉的解能捡回来尽量捡回来 (c 取一些特殊值)。 - 注意事项
- 通解
全部解 - 通解 + 奇解(考研超纲)
全部解 - 在线性方程中:通解
全部解
- 通解

「一阶」可化为变量可分离型 y' = f(ax + by + c)
- 换元之后,两端对
求导,转换成变量可分离型,将 , 归类,两端积分 
可化为变量可分离型 举例

- 奇解(考研不考,超纲)
「一阶」可化为变量可分离型 齐次方程

例题 可化为变量可分离型 齐次方程
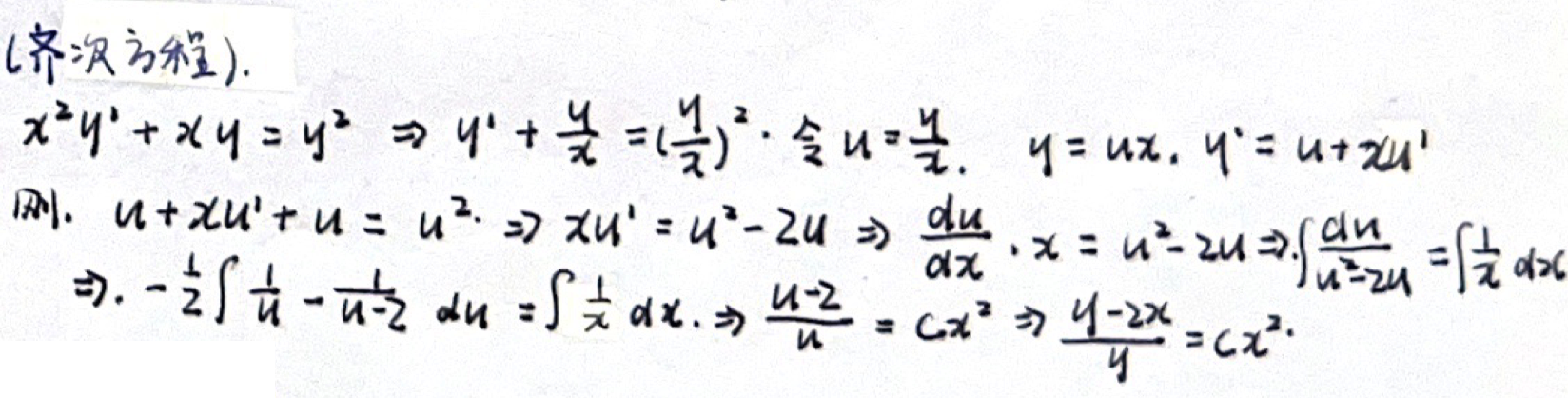
「一阶」 线性方程
两端同乘 (积分因子), - 解法:使用 公式:
- 一阶线性非齐次通解
- 一阶线性齐次通解,特别
时,有
- 一阶线性非齐次通解
注意事项
- 线性方程中求出来的通解一定是全部解
- 在线性方程中使用公式法,
可以不加绝对值 ,因为正负号相消
公式是如何计算出来的?

「一阶」 伯努利方程
伯努利方程转化为线性方程的过程
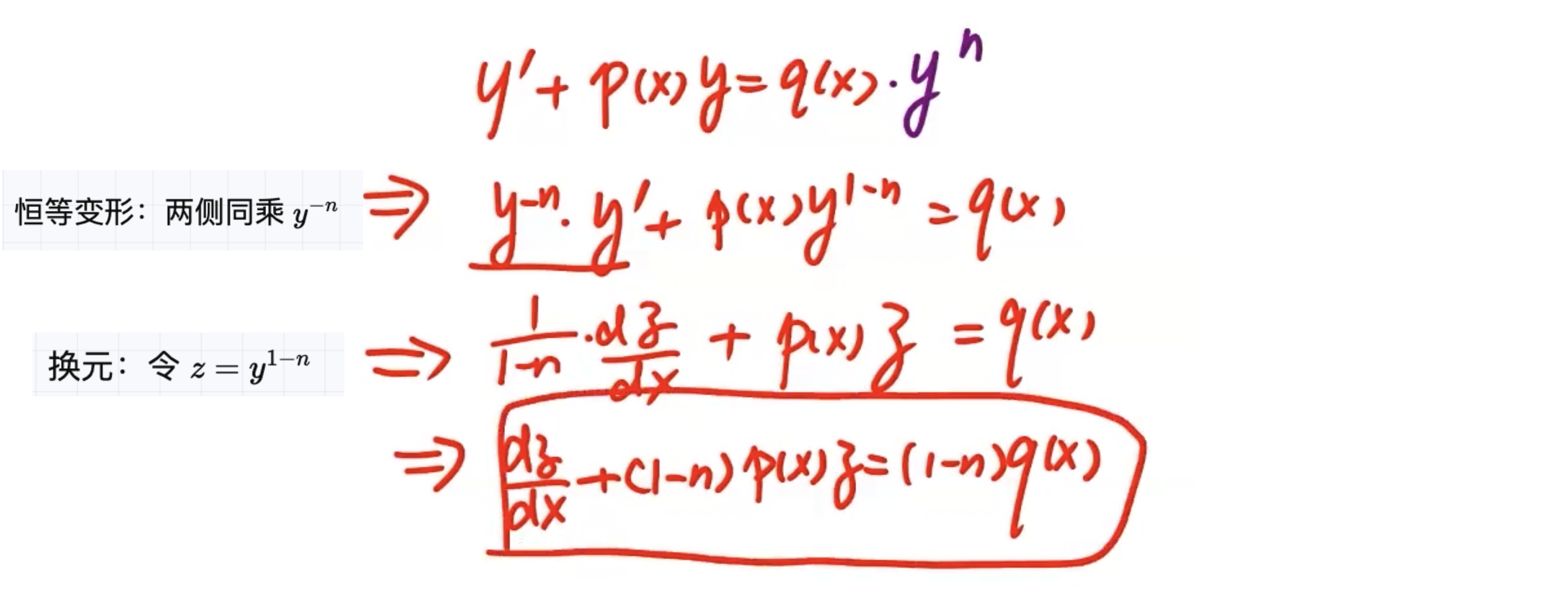
注意事项
- 当
时,方程变为一阶线性方程 - 当
时,方程变为一阶变量可分离方程
- 当
「一阶」 全微分方程
- 偏微分
- 凑微分
- 线积分
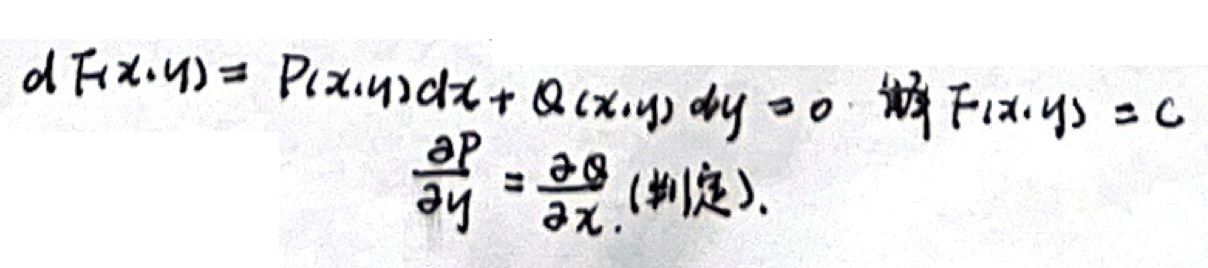
「二阶 > 一阶」可降阶 y‘’ = f(x, y')(缺 y)
- 把
全部换掉,赶尽杀绝

例题 缺
- ex1

- ex2
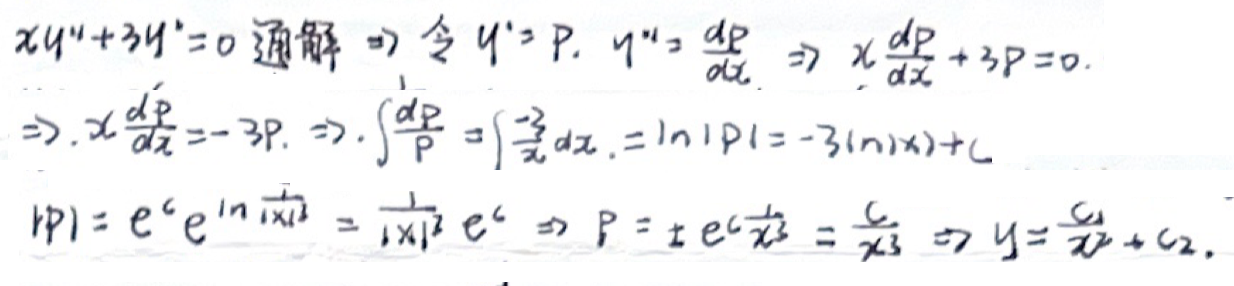
- ex3

「二阶 > 一阶」可降阶 y‘’ = f(y, y')(缺 x)⭐️
- 对
斩草除根

缺
- ex1

- ex2

「高阶」变系数、常系数方程
| 二阶变系数线性微分方程 | ||
|---|---|---|
| 齐次方程 | ||
| 非齐次方程 |
| 二阶常系数线性微分方程 | ||
|---|---|---|
| 齐次方程 | ||
| 非齐次方程 |
「高阶」通解及特解公式
| 方程 | 解的公式 |
|---|---|
| 齐次方程 | 通解: 两个线性无关的齐次特解之和 |
| 非齐次方程 | 通解: 非齐次的一个特解与两个线性无关齐次特解之和 |
| 两个非齐次方程之和 的特解 | 特解之和仍为特解: 两个非齐次方程的特解之和 |
「高阶 & 二阶」常系数齐次 通解与特征根 ⭐️
| 二阶常系数齐次线性微分方程的通解 对于 特征方程为 求特征根 | 特征根 | 通解 |
|---|---|---|
| 不等实根 | ||
| 相等实根 | ||
| 共轭复根 |
齐次通解 不等实根
- ex1

齐次通解 相等实根
- ex1

齐次通解 共轭复根
ex1
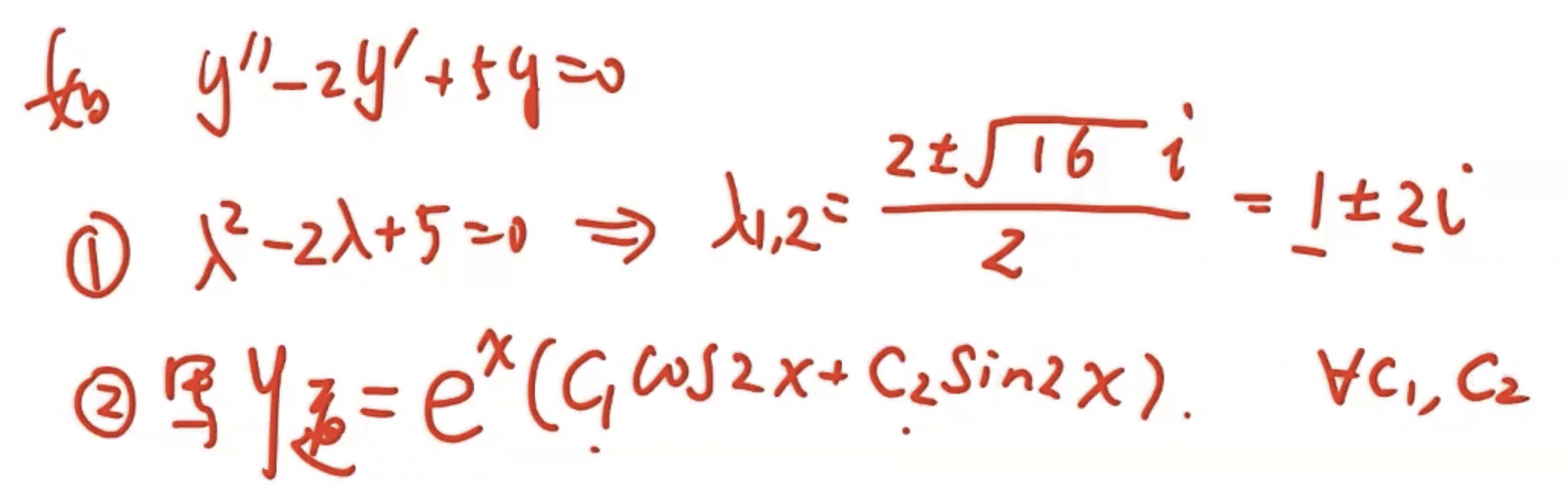
ex2

「高阶 & 二阶」常系数非齐次 特解与特征根
| 自由项 | --- | |
|---|---|---|
| 特解 | ||
| 求解步骤 | 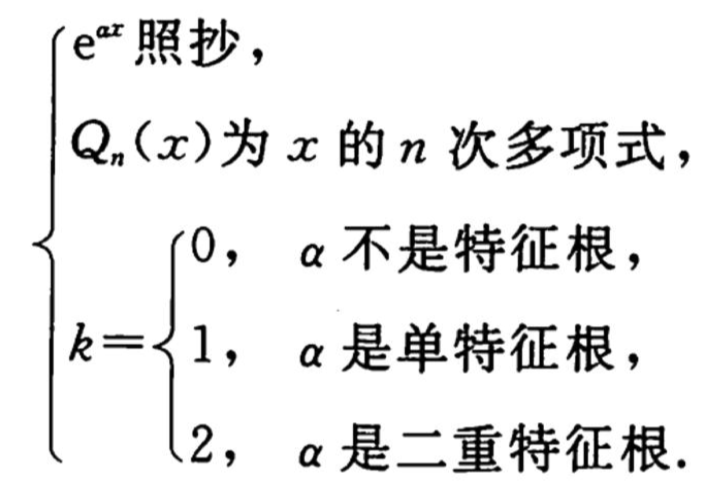 |  --- 1. 当 2. 当 |
- 左侧理论,右侧例题


自由项
- 左侧理论,右侧例题
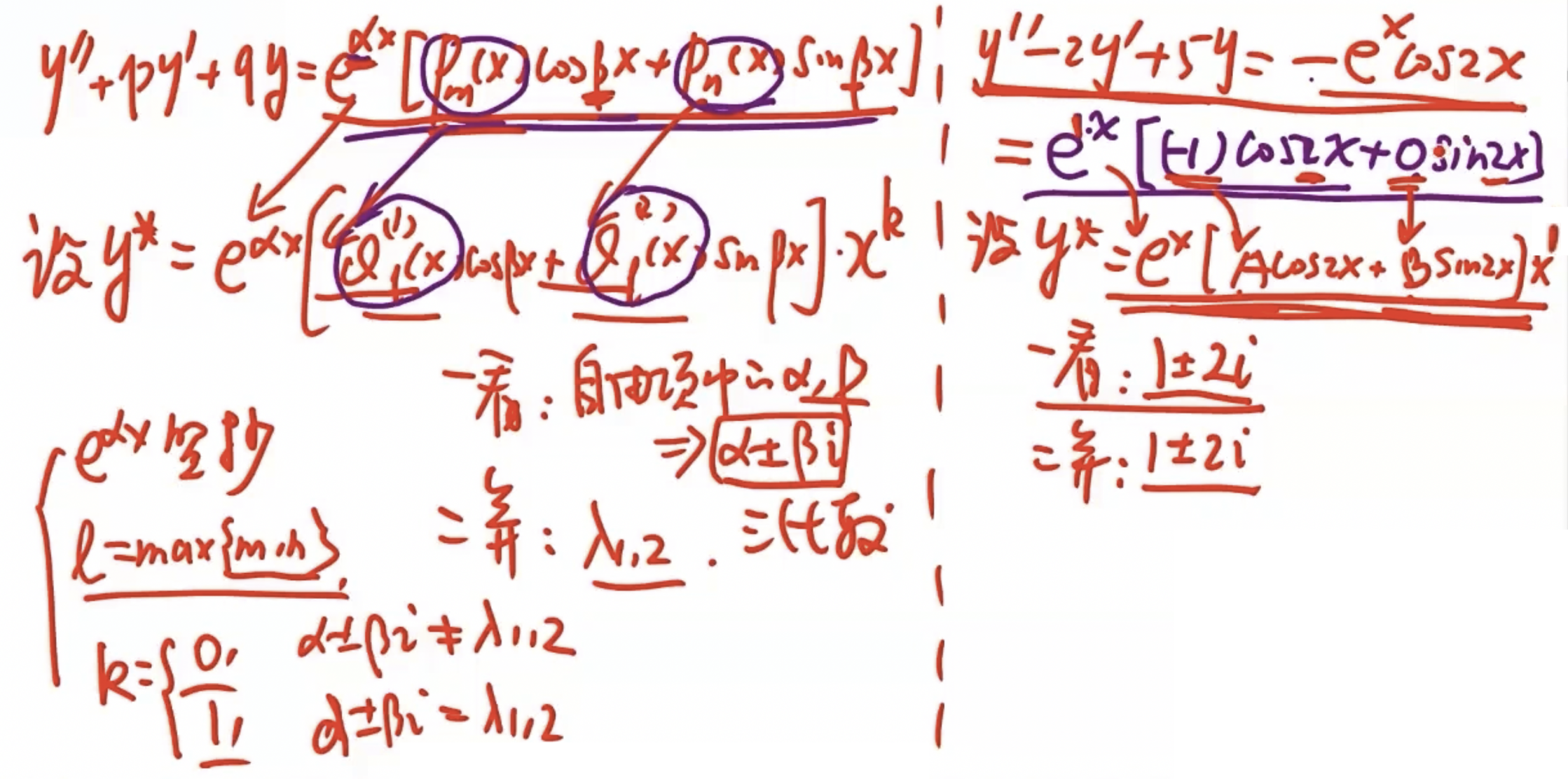
综合例题

「高阶」常系数齐次 通解与特征根
| n 阶常系数齐次线性微分方程 求 的特征根 | 微分方程通解 |
|---|---|
| (1)特征根为单实根 | |
| (2)特征根为 | |
| (3)特征根为单复根 | |
| (4)特征根为 (太复杂,考研不太可能会考) |
「例题」常系数齐次线性微分方程 通解应用

「高阶」欧拉方程 非重点
| 欧拉方程 | |
|---|---|
| 解法 | 令 |
例题 欧拉方程 转化为 常系数线性方程


