白昼幻想知识库

Appearance

X.题型汇总 ​

函数 ​

「复合函数」求定义域值域 ​

  • 三步走：1. 广义化 2. 画图分析 3. 写答案

复合函数求定义域及值域

image.png

数列极限 ​

「计」定义证明数列极限 ​

  • 用定义证明limn→∞qn=0（ q 为常数且|q|<1）

image.png

「计」定义加不等式证明数列极限 ​

  • 证明limn→∞an=A，则limn→∞|an|=|A|

image.png

「方」证数列极限为0，先证其绝对值极限为0，后夹逼 ​

image.png

奇数次数列展开时不可少项 ​

  • 数列limk→∞x2k+1 展开时不可少项 image.png

数列极限的四则运算规则 ​

数列极限加减法，整体极限不可拆

image.png

(无穷-无穷)是未定式，不符合极限运算规则 ​

image.png

遇到递推式 用单调有界准则 证明极限存在 ​

image.png

中值定理 ​

「计」函数闭区间连续、开区间可导 ​

image.png

「题」闭区间连续，开区间可导，罗尔定理 ​

image.png

image.png

image.png

image.png

「题」拉格朗日中值定理的使用 ​

image.pngimage.png

image.png

「⭐️」介值定理、拉格朗日中值定理综合题 ​

image.png

「题」柯西中值定理的使用 ​

image.png

「计」泰勒公式的使用 ​

image.png

「题」导数介值定理（做答案、记结论） ​

image.png

导数与微分 ​

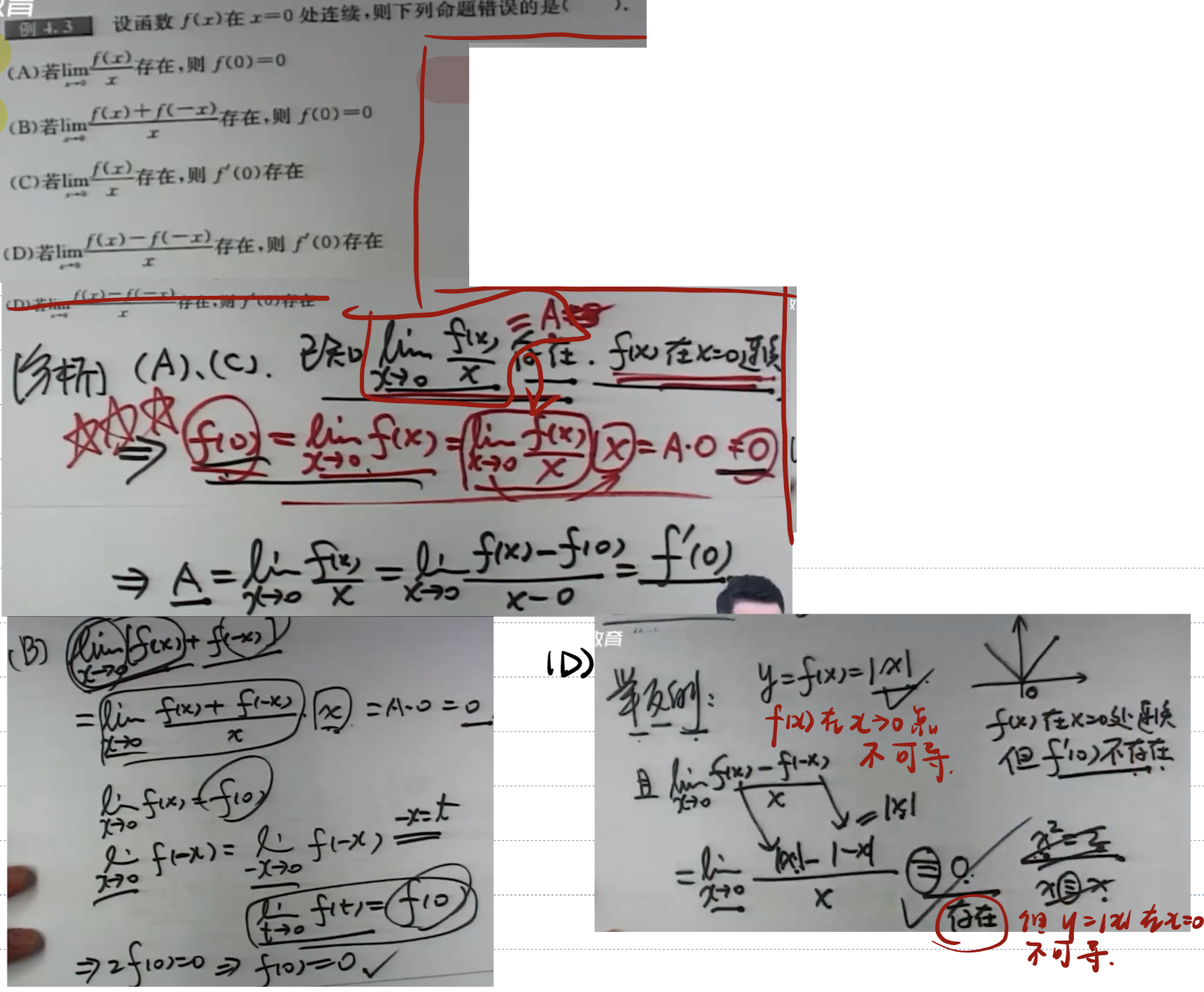
「记」连续函数用定义求导数 ​

image.png

「计」连续函数用导数定义求导数 ​

  • f(x) 在极限点
    • 如若可导，极限可拆
    • 若不可导，极限不可拆

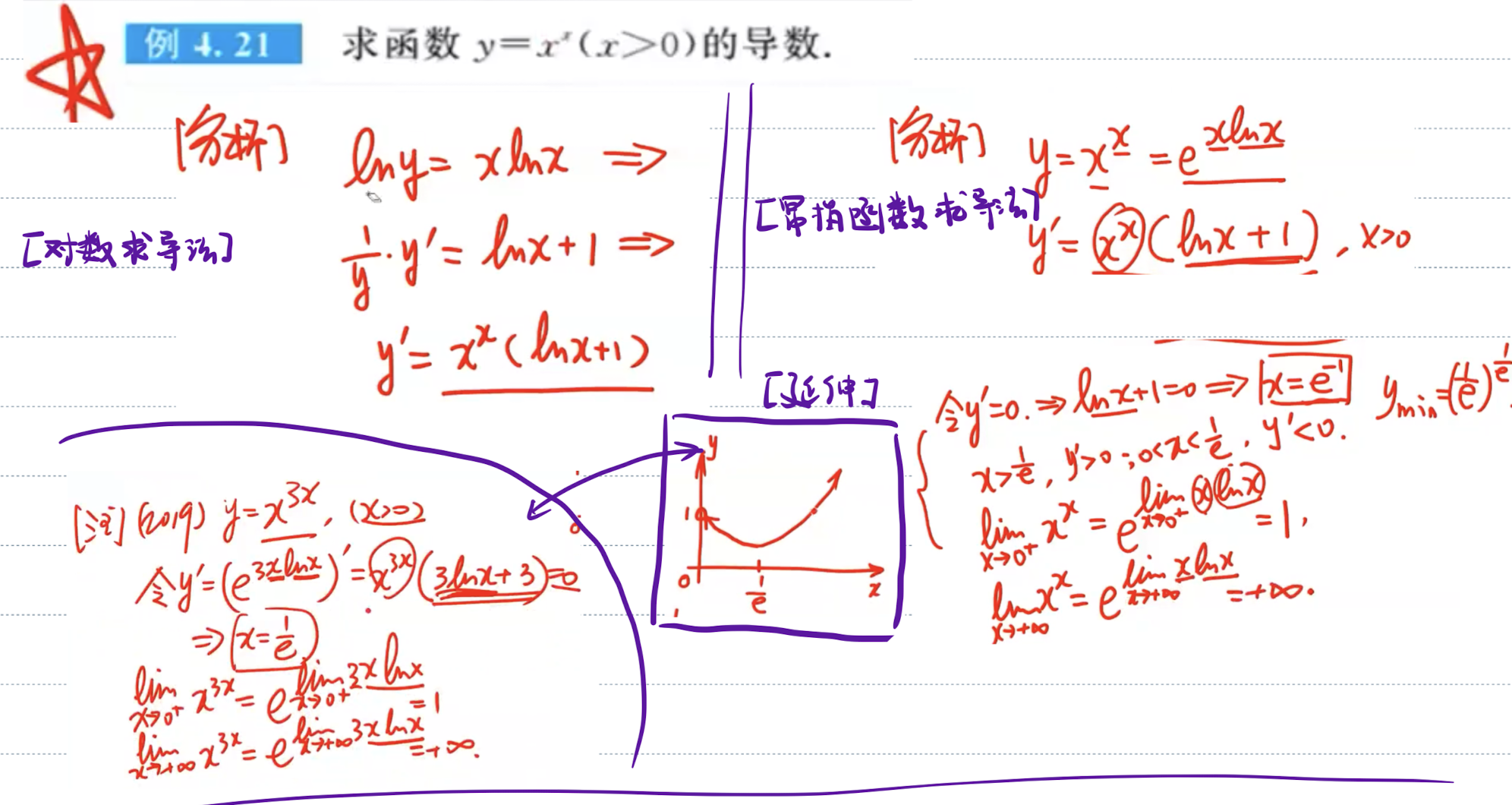
image.png

分别用对数、幂指函数求导法解题 ​

image.png

高阶求导 归纳法 选择题迅速求三阶导找规律 ​

image.png

泰勒、麦克劳林公式在高阶导数中的应用 ​

image.png

「计」y = 1/x 的 n 阶导数 ​

image.png

导数应用 ​

「计」极值点与拐点的判别只需要函数连续 ​

image.png

「计」求最大值和最小值 ​

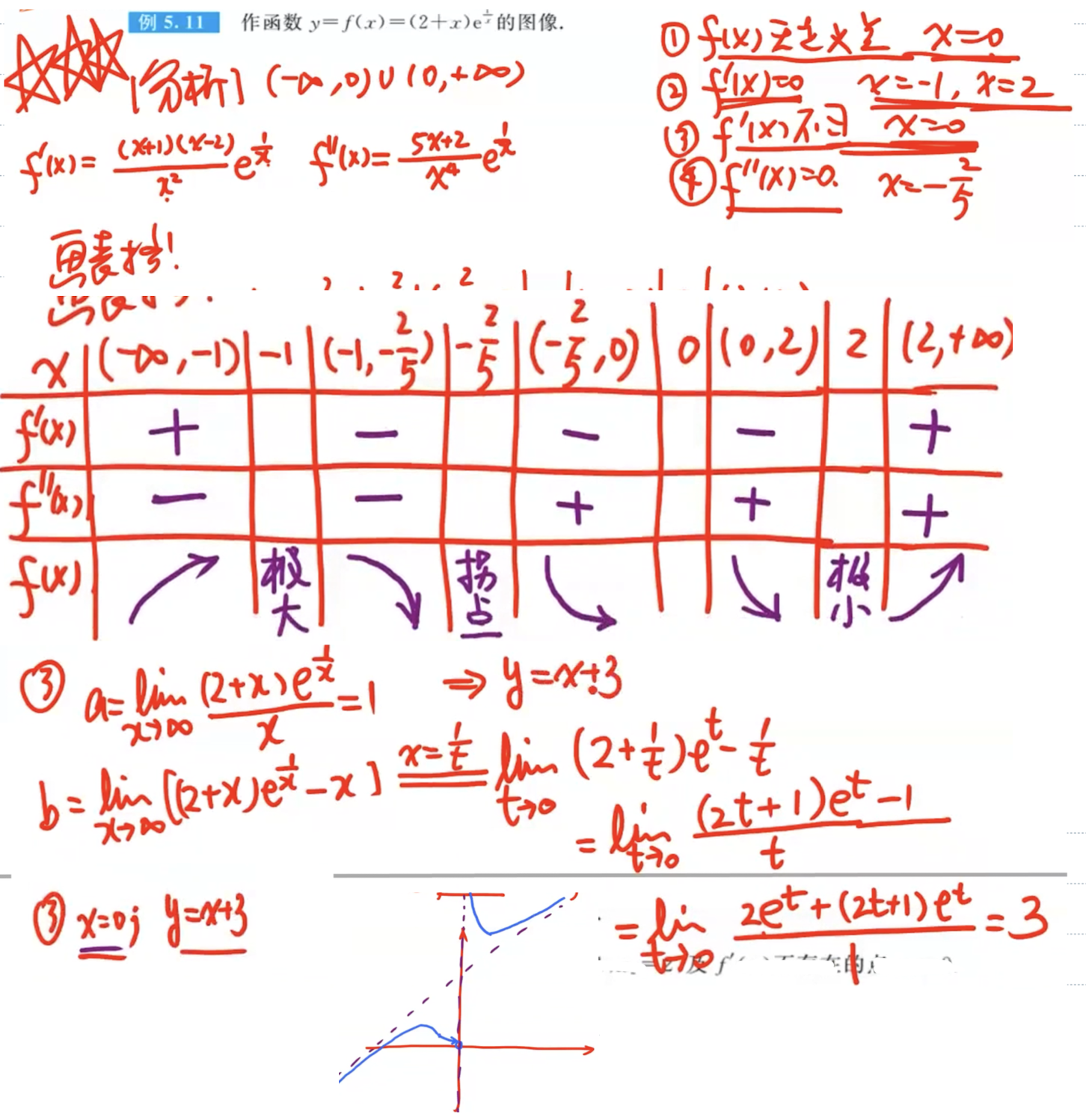
image.png

「计」求数列最大值 ​

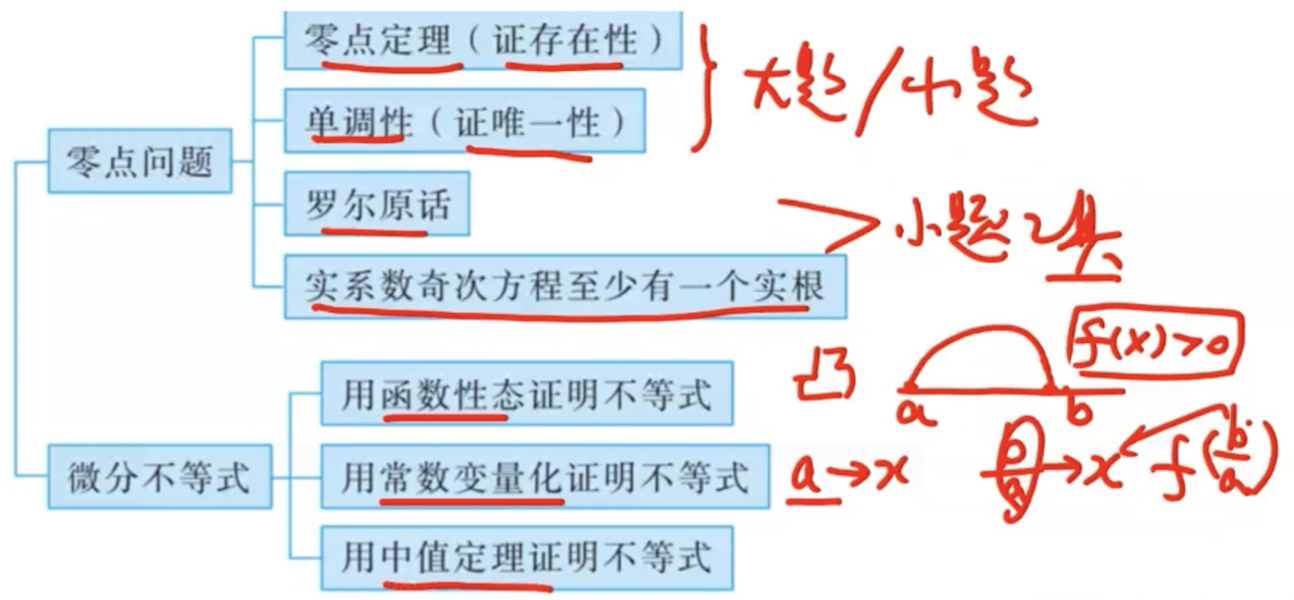
image.png

「计」做函数图像 ​

image.png

image.png

零点定理（主要用于证明根的存在性） ​

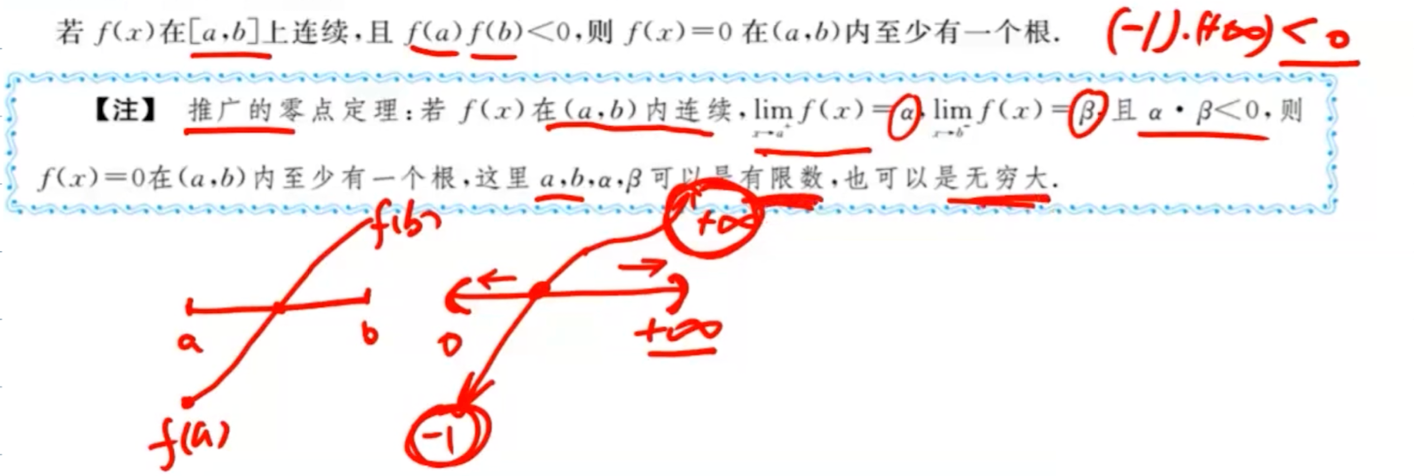
image.png

单调性（主要用于证明根的唯一性） ​

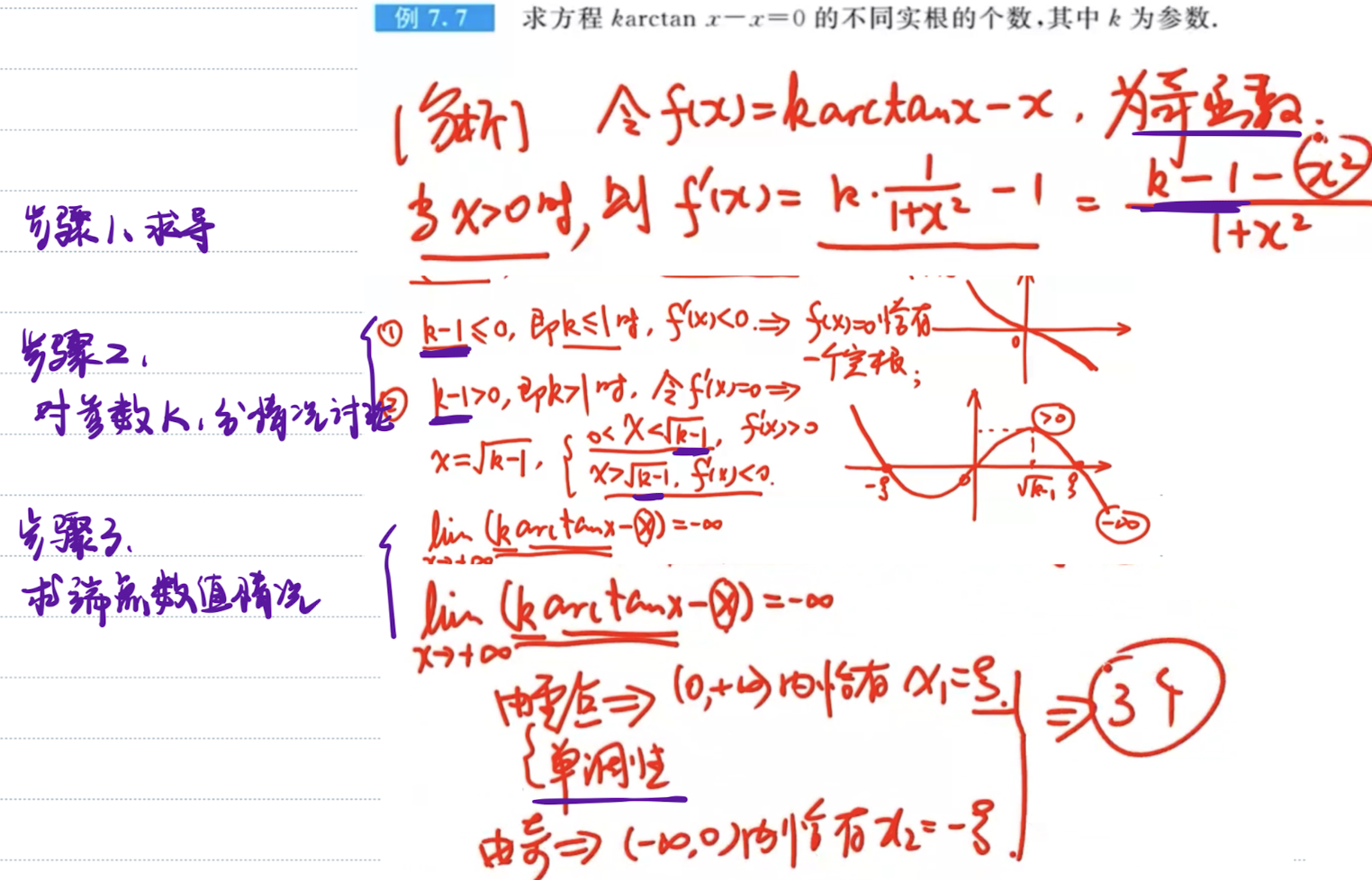
image.png

零点问题中导数含不含参数的两种情况 ​

image.png

「题」导数中不存在参数k的情况 ​

image.png

「题」导数中含有参数k的情况 ​

image.png

罗尔原话（罗尔定理的推论） ​

定理image.png
证明image.png

实系数奇次方程至少有一个实根 ​

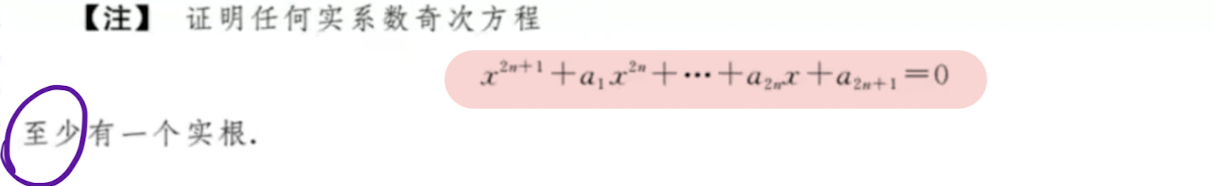
image.png

「题」计算高次函数导数零点个数 ​

image.png

image.png

微分不等式 ​

用函数性态（包括单调性、凹凸性、最值等）证明不等式 ​

image.png

「题」函数性态证明不等式 ​

image.png

利用凹凸性证明不等式 ​

image.png

「题」凹凸性证明不等式 ​

image.png

image.png

用中值定理证明不等式 ​

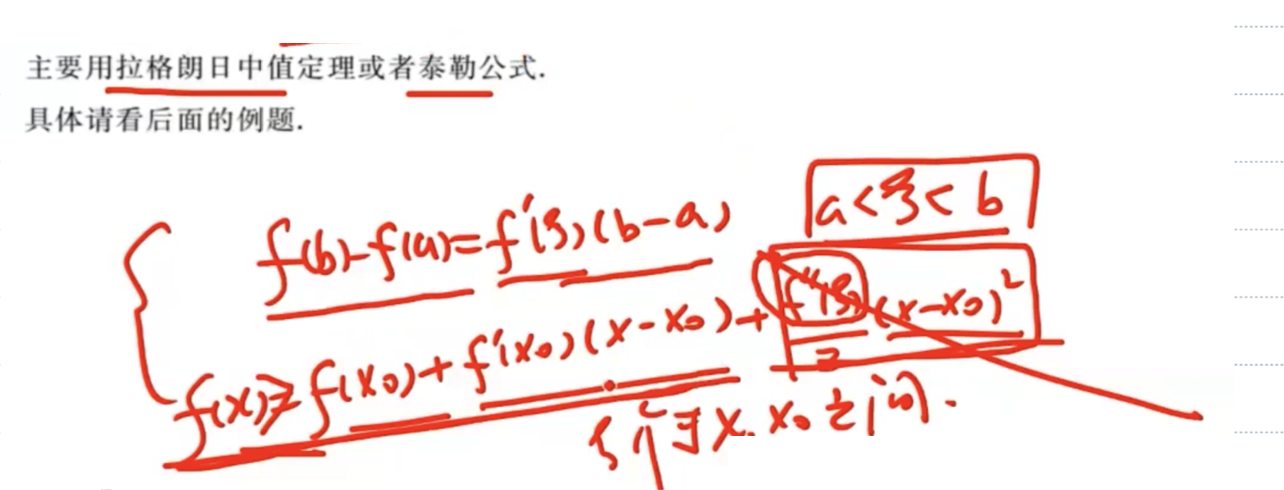
image.png

「题」拉格朗日中值定理+放缩法 ​

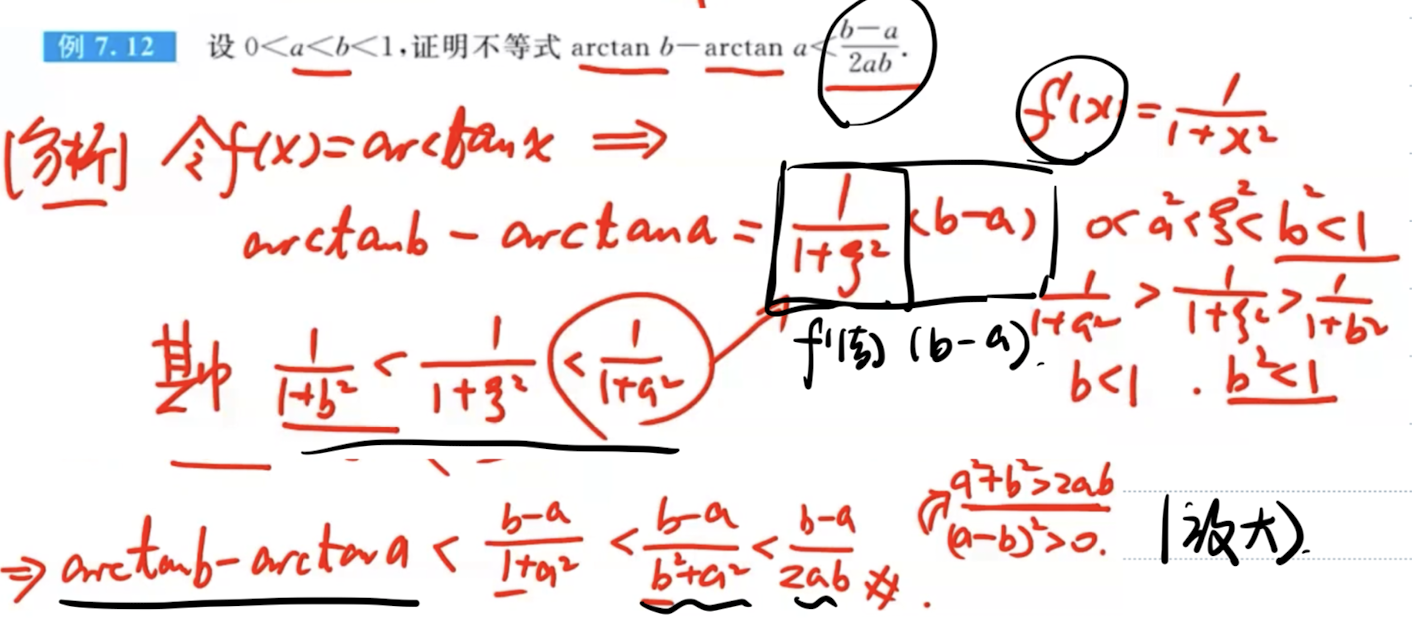
image.png

「题」泰勒公式/三次拉格朗日 ​

  • 泰勒公式

image.png

  • 三次拉格朗日 image.png

原函数和不定积分 ​

image.png

「题」全体原函数（积分） ​

image.png

「题」在同一个周期上的积分值与起点无关 ​

预备定理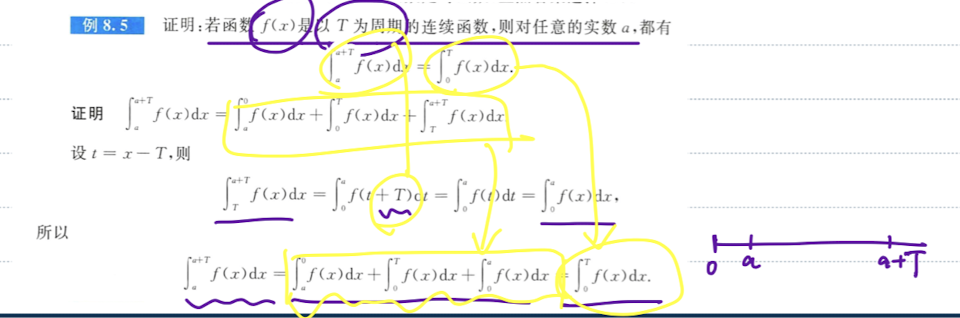image.png
image.png

定积分 ​

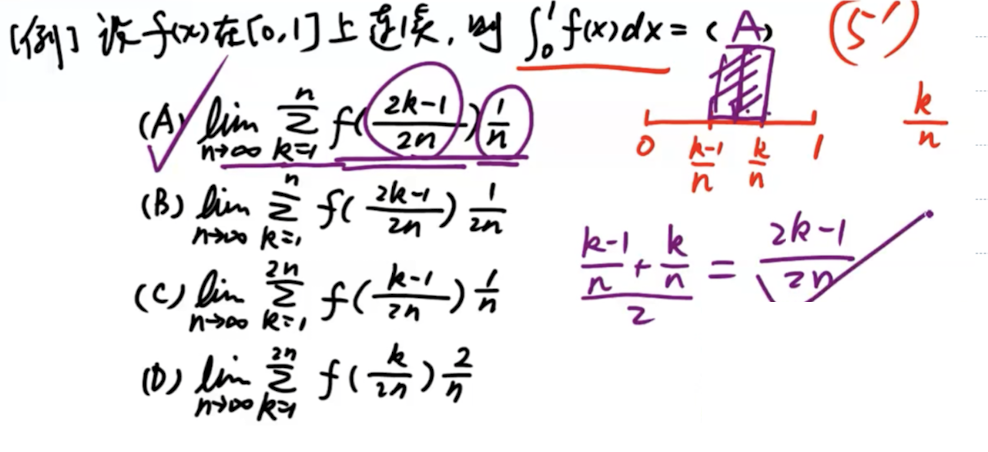
「⭐️」凑定积分定义 ​

夹逼准则 对于n项和极限，不能凑出定积分定义，就用夹逼准则 ​

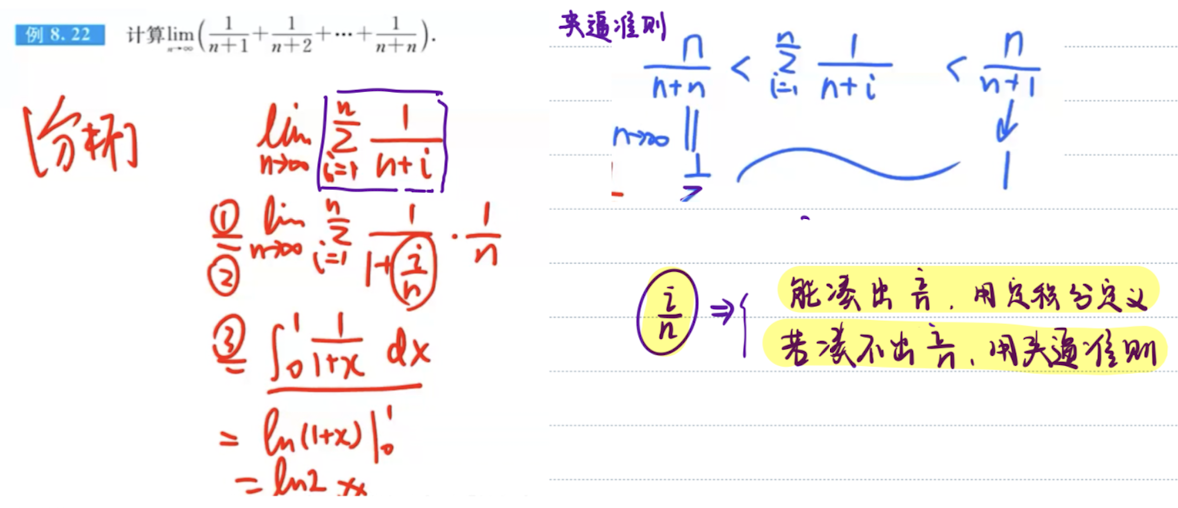
image.png

定积分定义 ​

image.png

取左端点/中点高 ​

image.png

反常积分 ​

image.png

「题」利用P级数判别敛散性 ​

image.png

「记&题」P级数+比较思想 & 反常积分敛散性判别 ​

image.png

「记」讨论敛散性并【背结论】 ​

image.png

定积分的换元积分法 ​

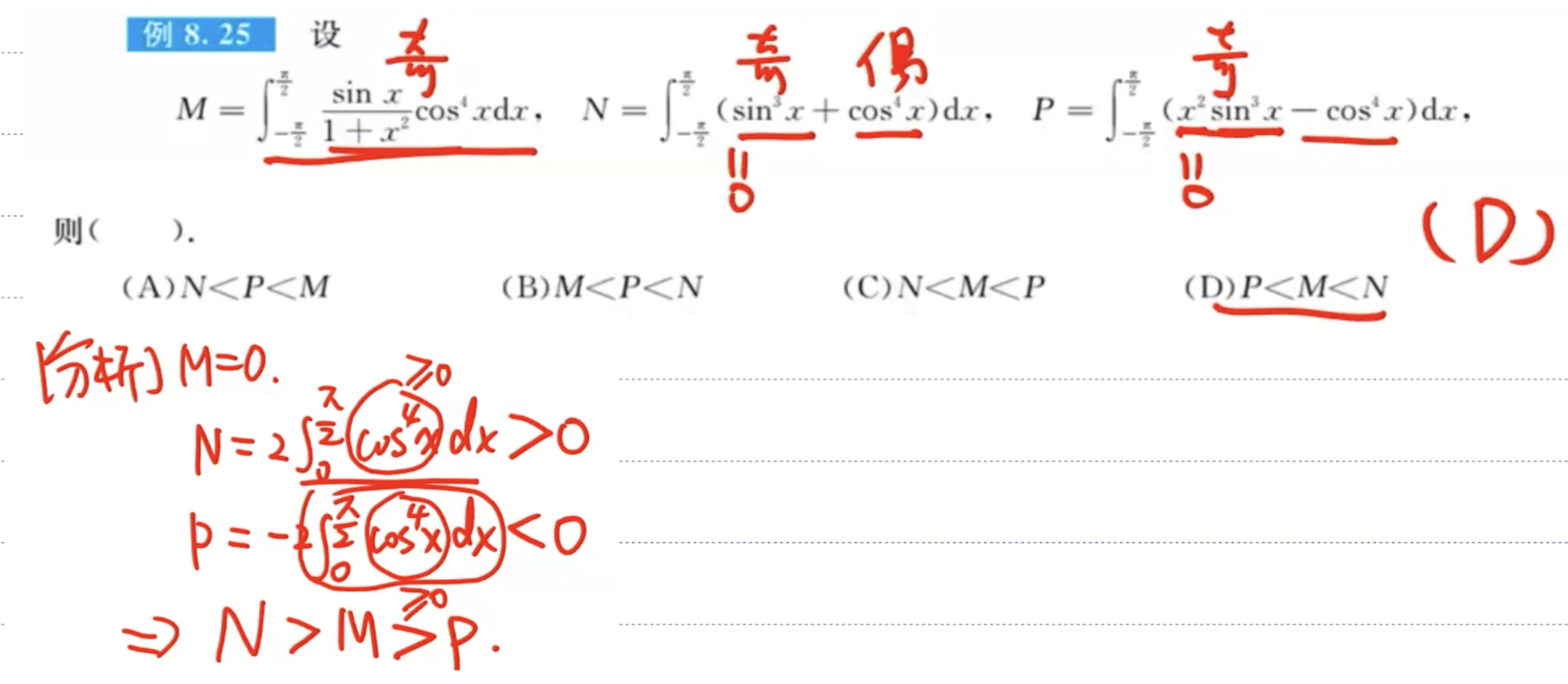
image.png

「题」奇偶型比较定积分大小 ​

image.png

区间再现公式求解定积分 ​

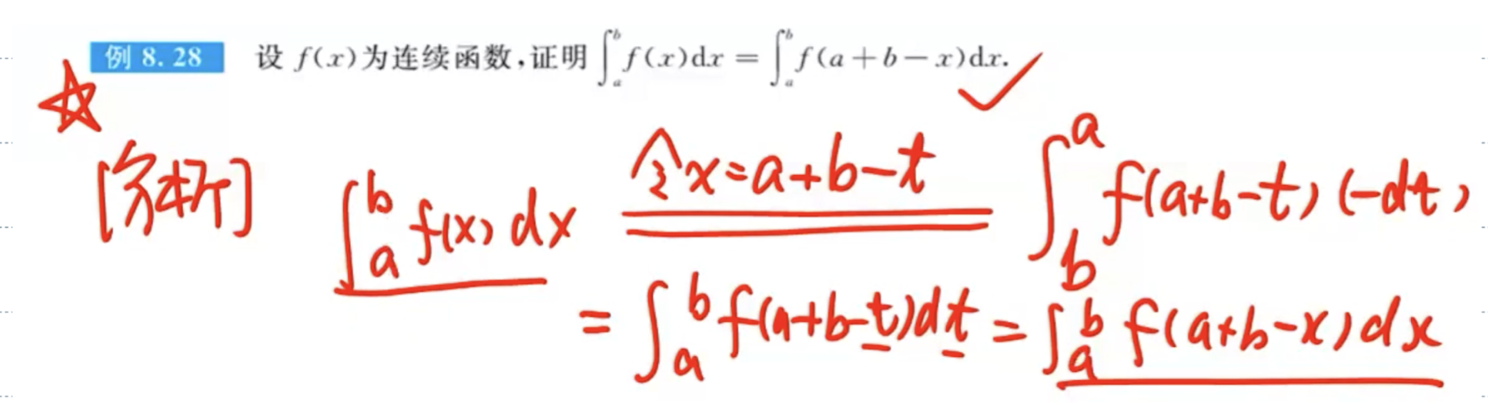
image.png

华里士公式求解高阶三角函数的定积分 ​

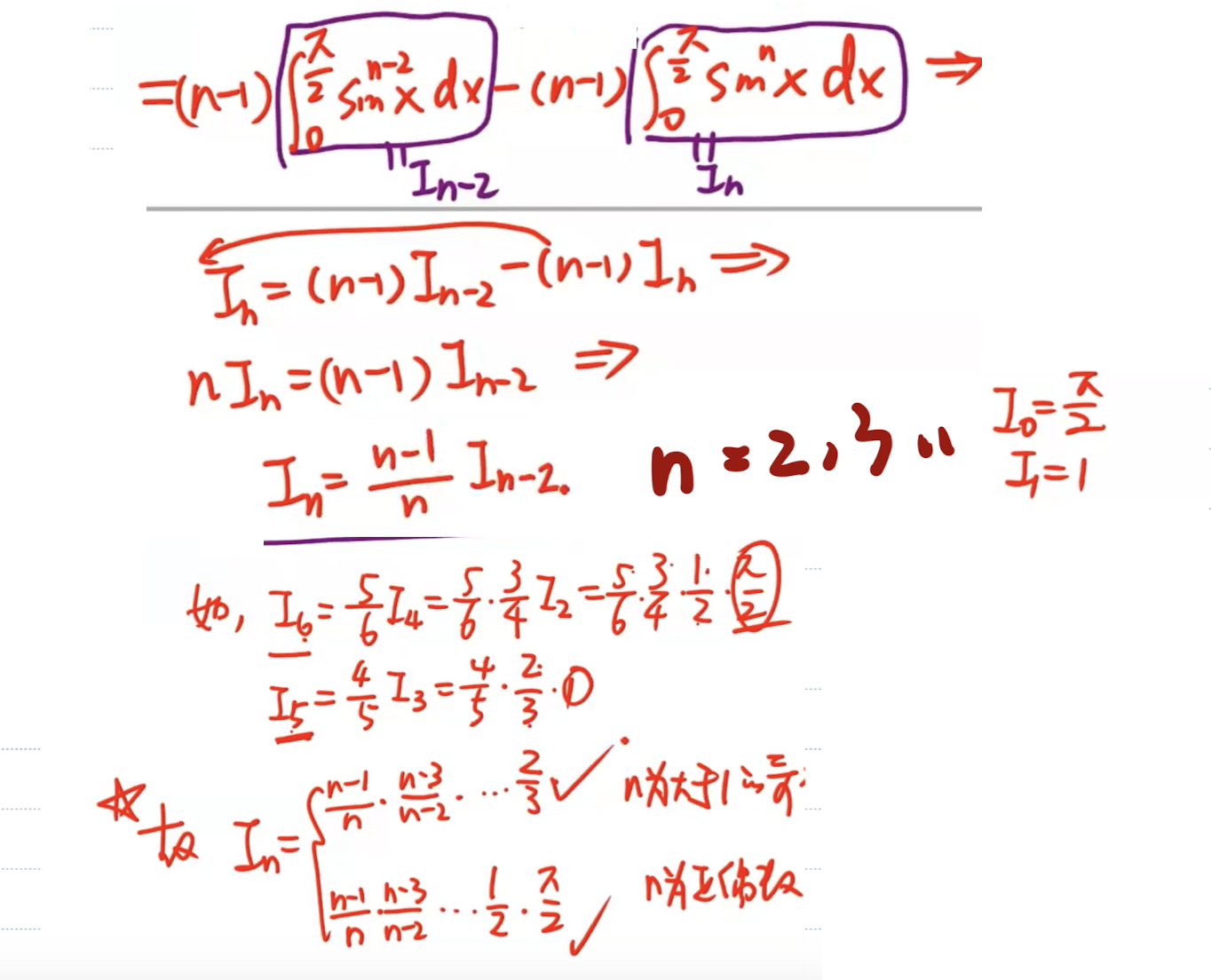
image.pngimage.png

「题」区间再现+华里士公式 ​

image.png

「题」若积分区间存在瑕点，单列出来 ​

image.png

「题」在收敛条件下，换元可实现反常积分和定积分的相互转化 ​

image.png

定积分的应用 ​

「伯努利双纽线」极坐标面积求法 ​

双纽线方程双纽线图像
直角坐标方程
(x2+y2)2=2a2(x2−y2)

极坐标方程
r2=2a2cos2θ
image.png

image.pngimage.png

「切线」切线方程的求法 ​

  • 切点的导数 = 切线的斜率 k

image.pngimage.png

「旋转体体积」绕指定直线旋转的旋转体的体积 ​

  • 若 封闭图形 D 绕 直线 y=1 旋转，相当于将封闭图形向下移动 1 后，绕 x 轴旋转
  • y 轴同理

image.pngimage.png

「旋转体体积」空心旋转体的体积&旋转体体积公式对 y 积分 ​

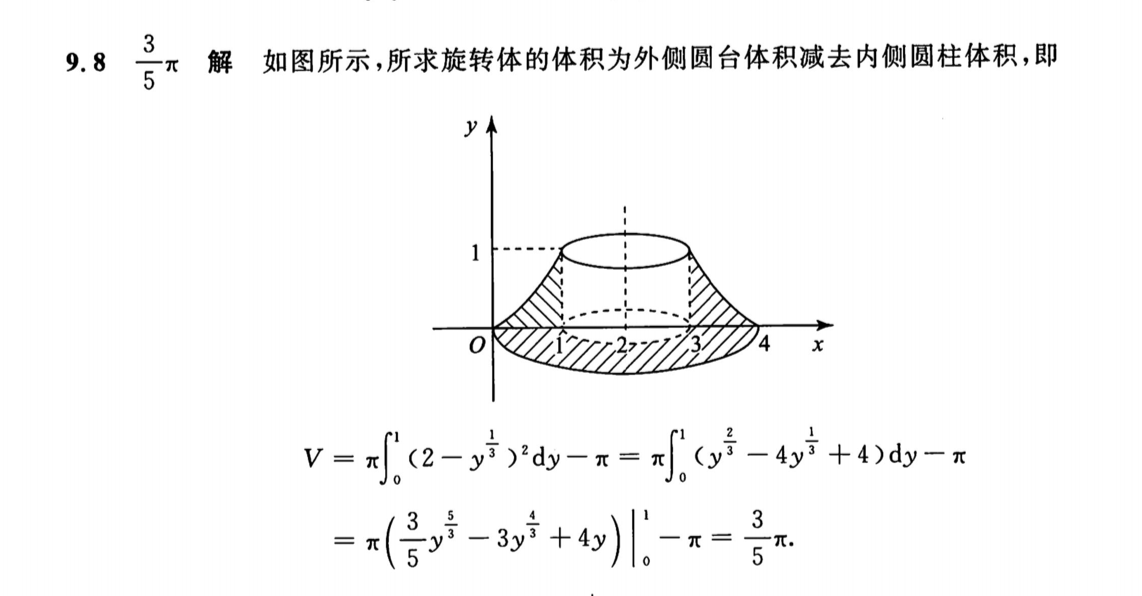
image.pngimage.png

「旋转体体积」旋转体方程中出现绝对值如何处理？ ​

image.pngimage.png

常微分方程 ​

「一阶&线性」分段函数 ​

分段函数

image.png

「一阶&线性」”恒等变形“化为已知类型 ​

TIP

image.png

「一阶&伯努利」字母互换、化为线性方程 ​

TIP

image.png

「一阶&线性」 一阶线性 -> 反函数 ​

TIP

image.png

「高阶&非齐次」通解及特解求法 ​

TIP

image.png

image.png

image.png

image.png

「计」不等式证明函数有界 ​

image.png

Copyright@ 2024 Alan White