A.公式汇总

细碎知识点

分母极限为零，则分子极限为零。
洛必达条件为
- 分子分母均在某点邻域内可导
- 该点分子分母的极限值为零或无穷
- 该点分子极限值比分母极限值存在或无穷
若函数一阶可导（处处可导），那么该函数只可以进行一次洛必达。。
若函数在某点处二阶可导，那么该函数一阶处处可导。

「记」双曲正弦、反双曲正弦、双曲余弦

反双曲正弦在 $(- 1, 1)$ 范围内与x轴围成的面积为 $S = \frac{1}{3}$

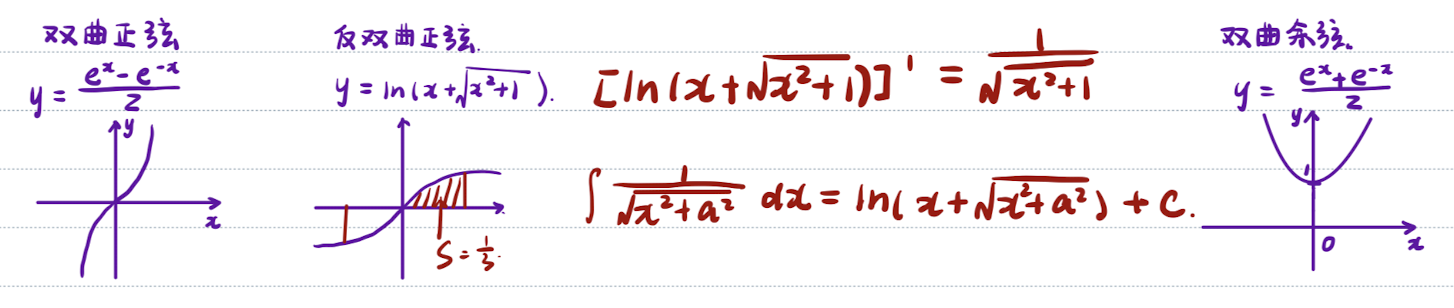
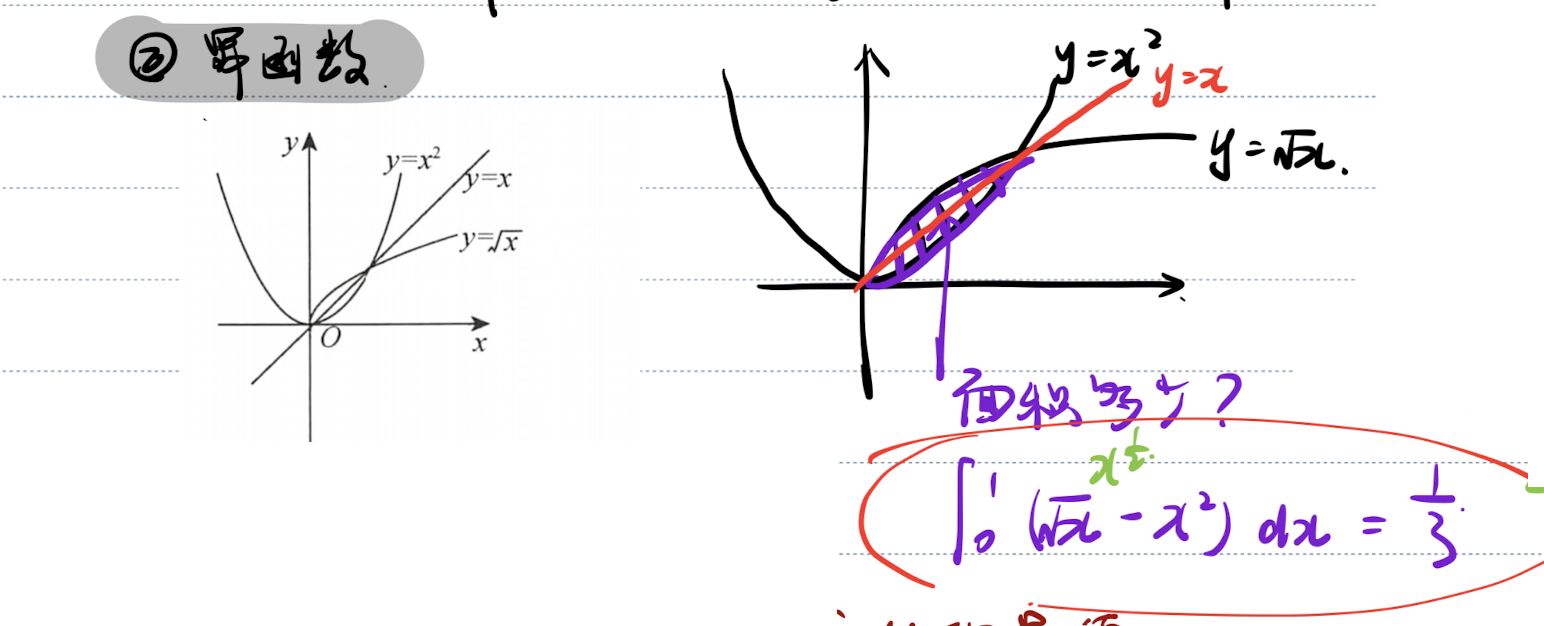
「记」幂函数相交面积

$y = x^{2}$ 与 $y = \sqrt{x}$ 相交面积为 $\int_{0}^{1} (\sqrt{x} - x^{2}) d x = \frac{1}{3}$

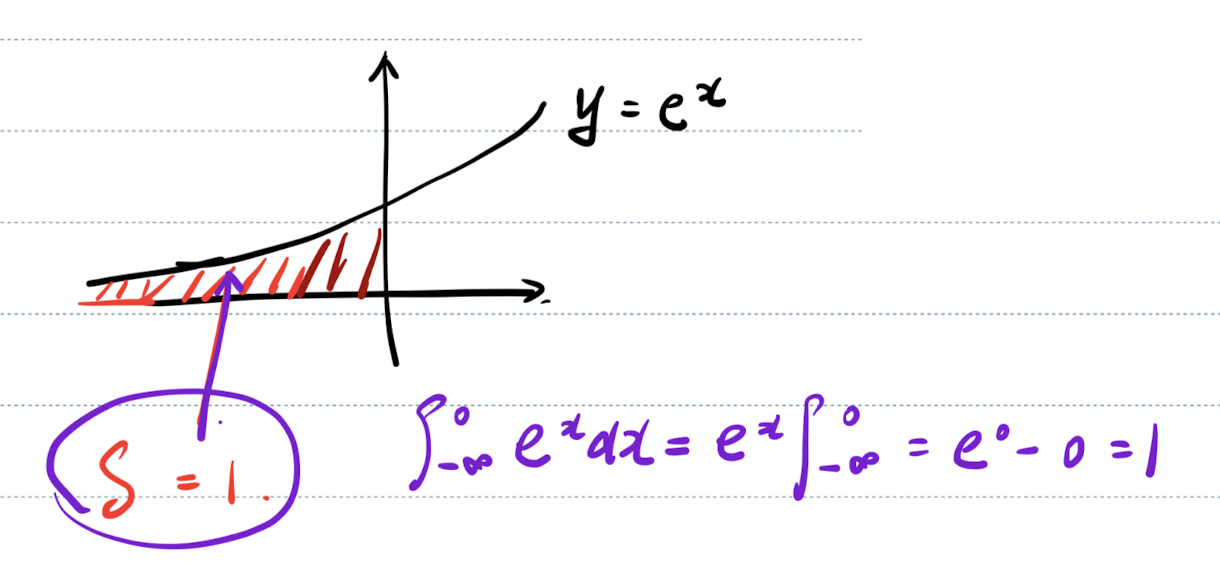
「记」指数函数相交面积

指数函数 $y = e^{x}$ 在区域 $(- \infty, 0)$ 面积为 $S = 1$

「记」快速计算三角函数面积

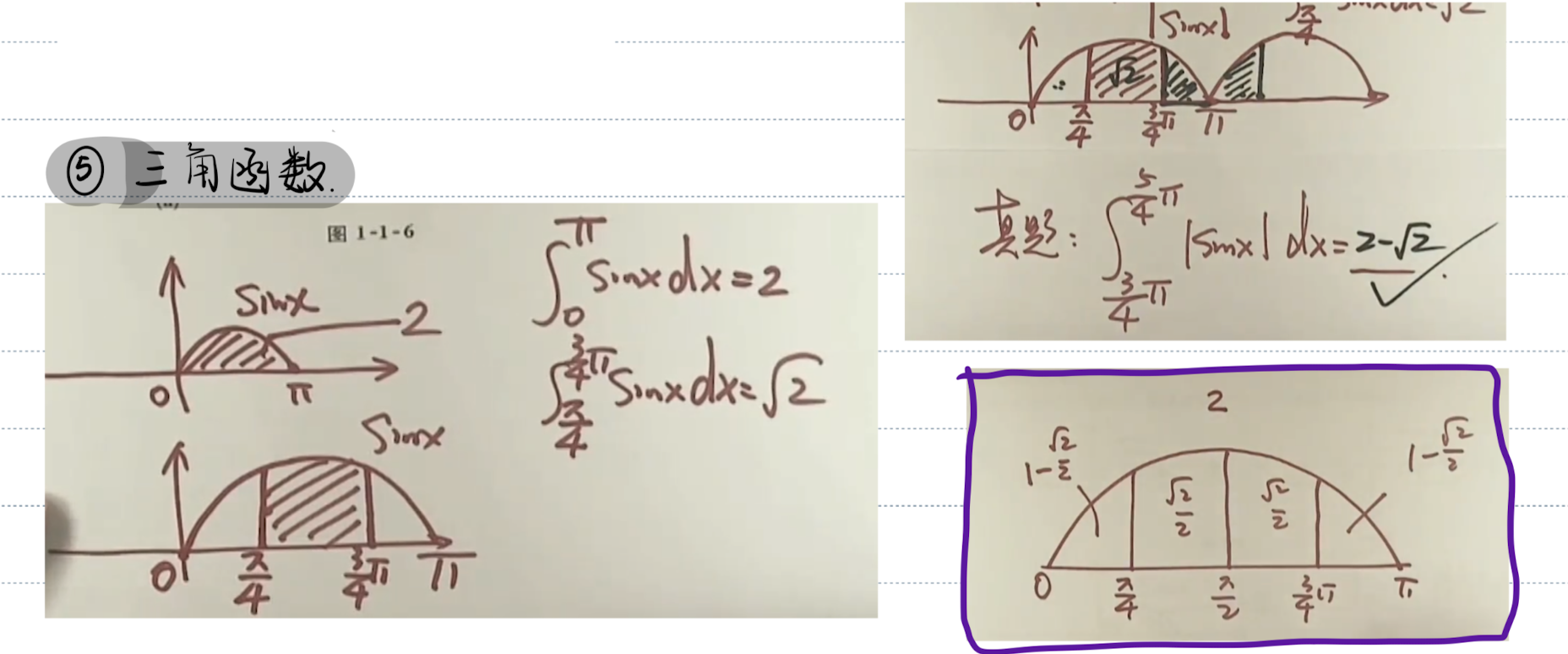
「记」各三角函数之间的关系图

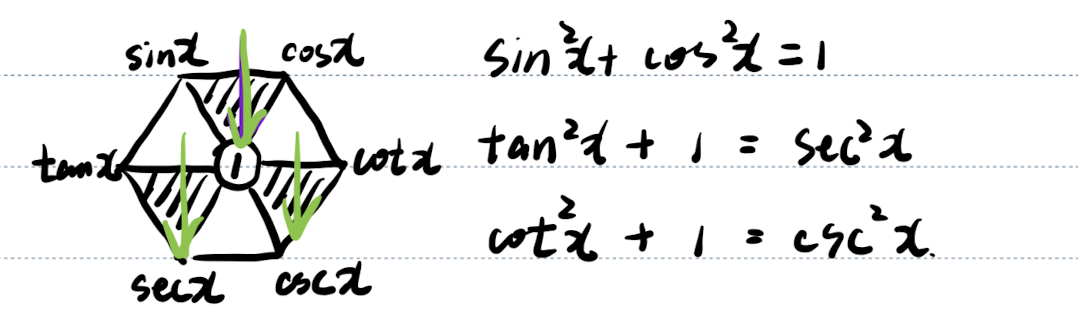
「记」反三角函数计算总结

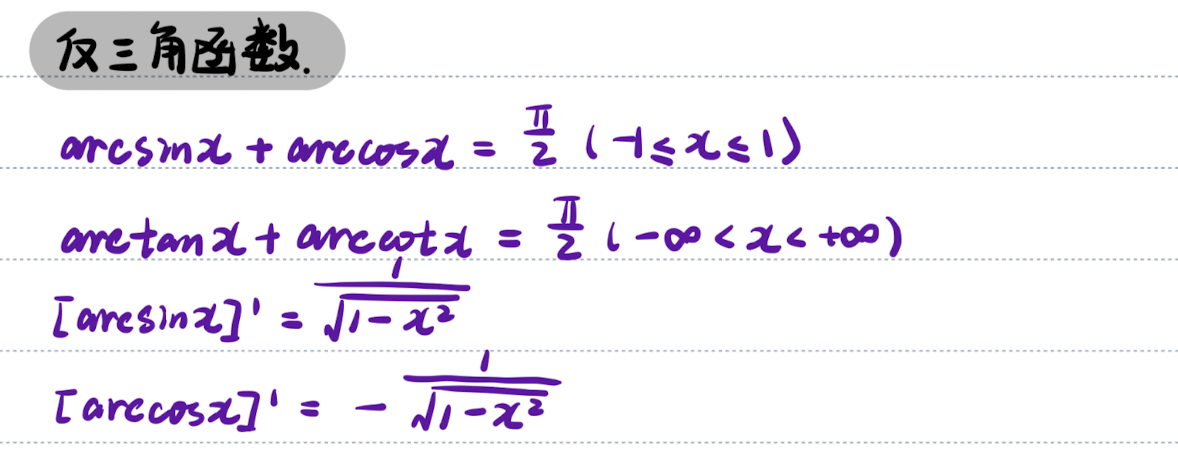
「记」摆线方程

摆线（平摆线）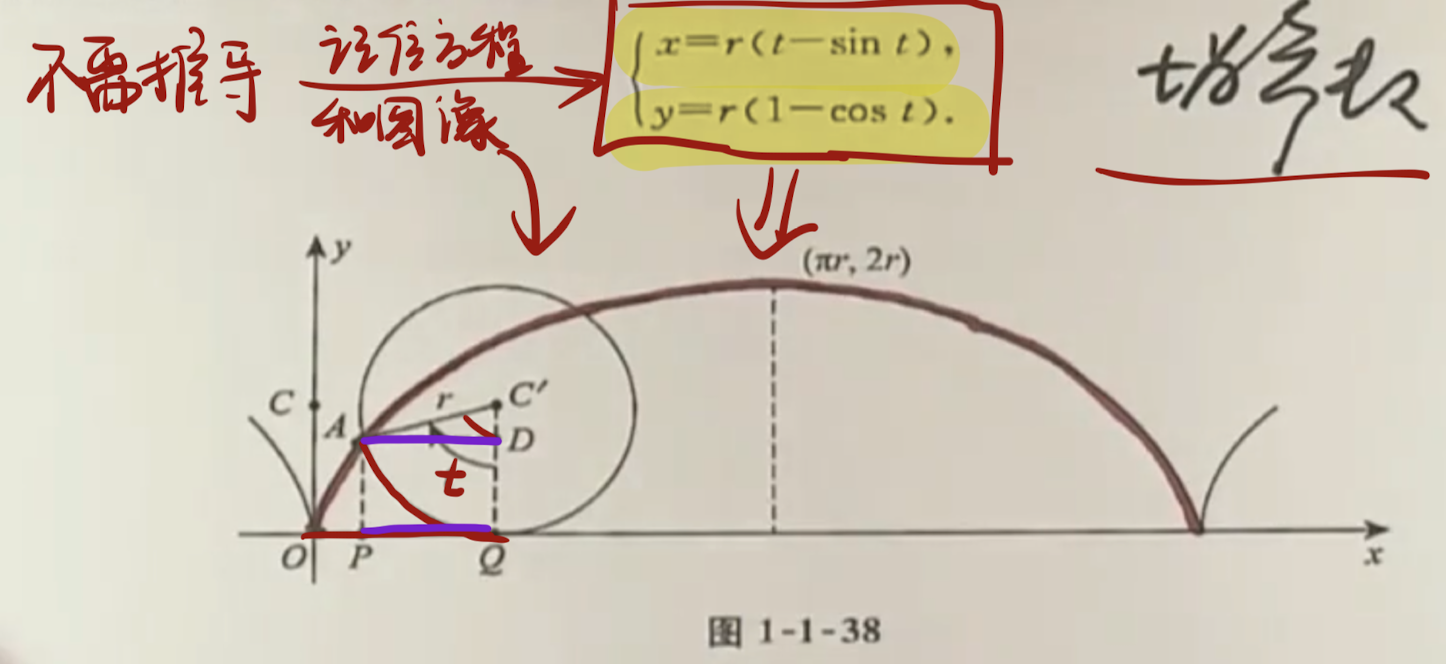
星形线（内摆线）
汇总

「记」等差、等比、n项和数列公式

数列	公式
等差数列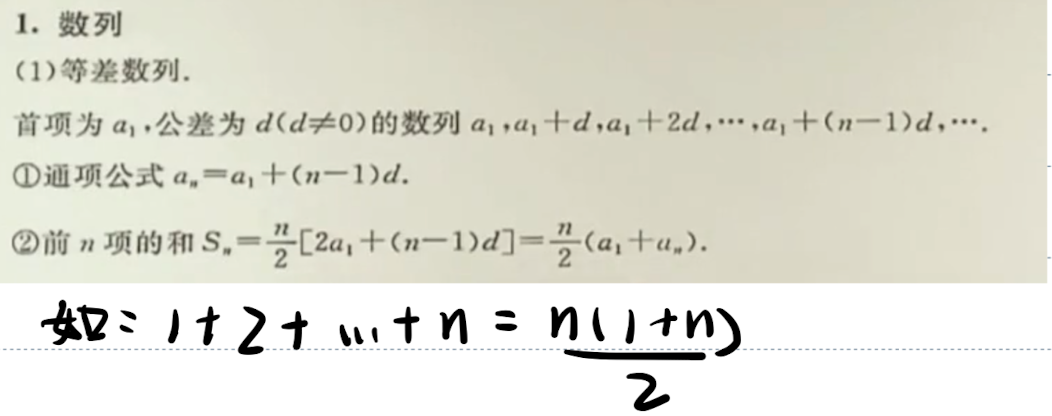
等比数列
常见数列前n项和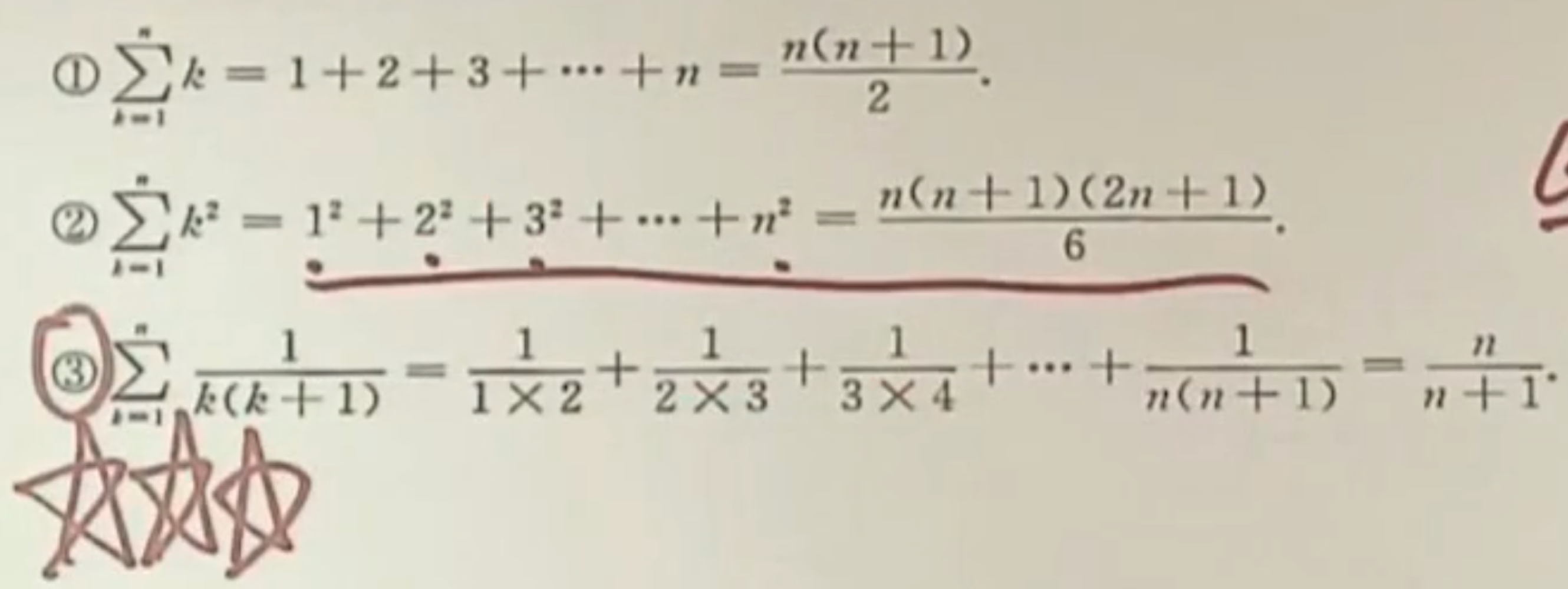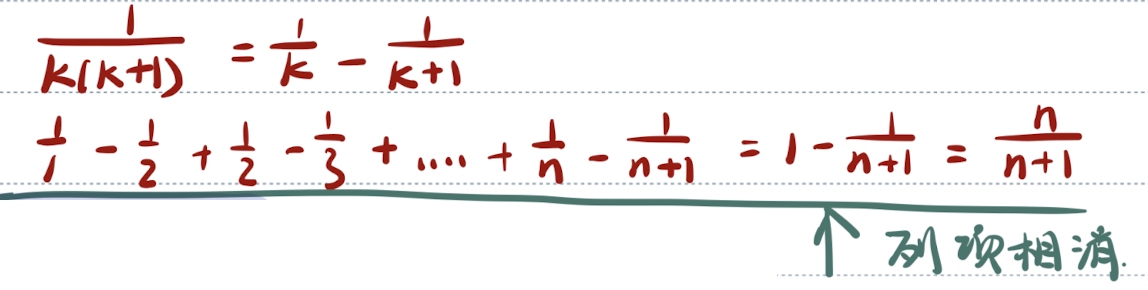

「记」三角函数基本关系


三角函数基本关系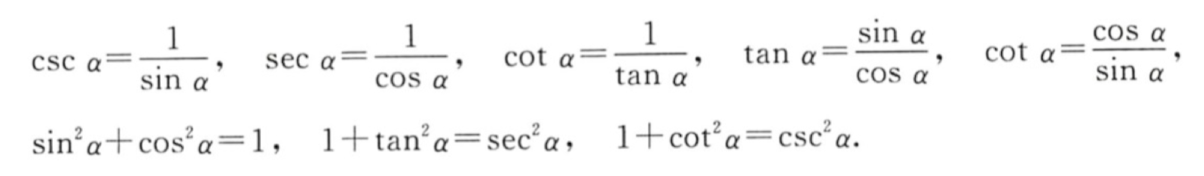
小结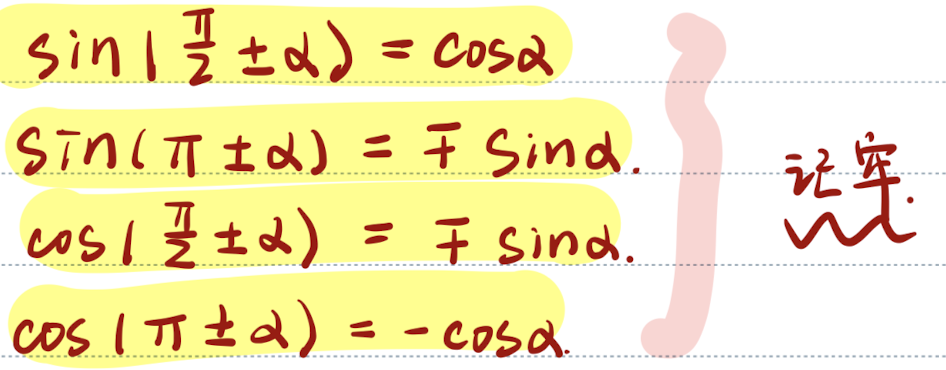

「记」三角函数重要公式

倍角公式
半角公式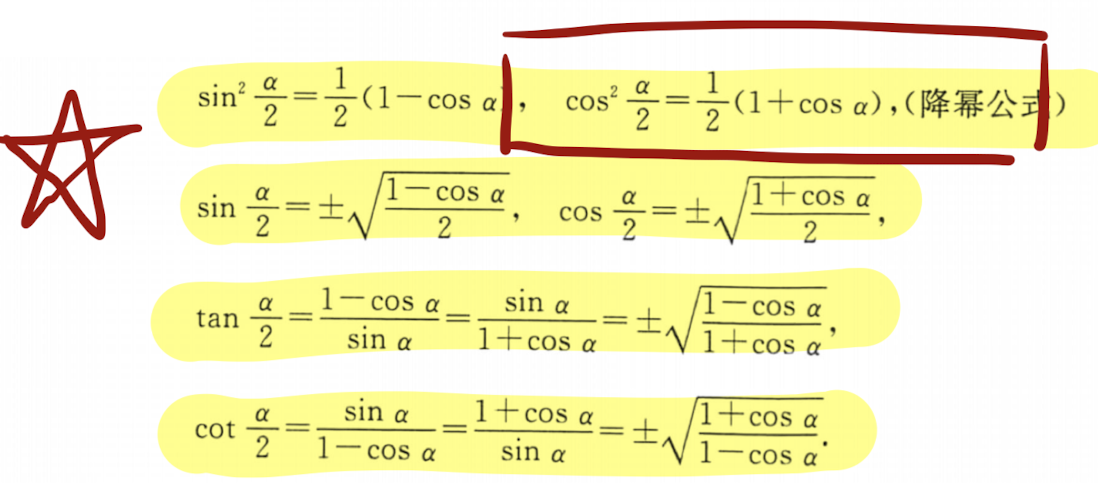
和差公式
积化和差公式、和差化积公式（考前背）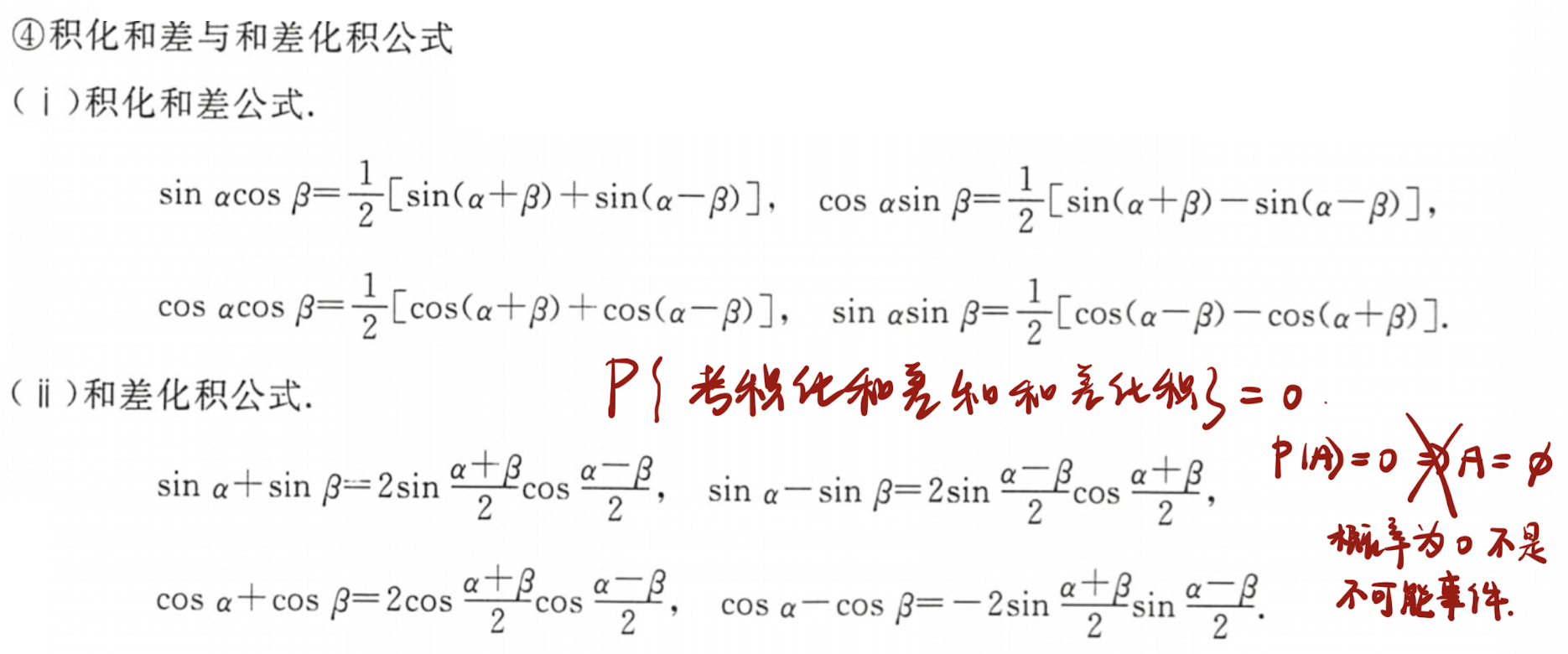
万能公式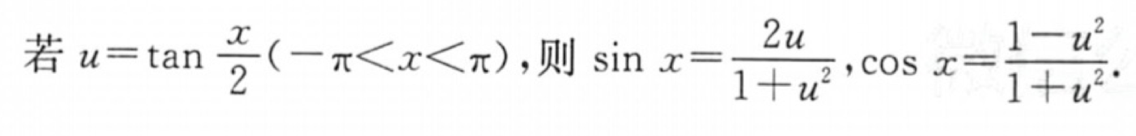

「记」对数运算常考公式

「记」一元二次方程基础

一元二次方程
根的公式
根与系数的关系（韦达定理）
根的判别式、共轭复根
抛物线顶点

「记」因式分解公式

「记」阶乘与双阶乘

「记」华里士公式（点火公式）

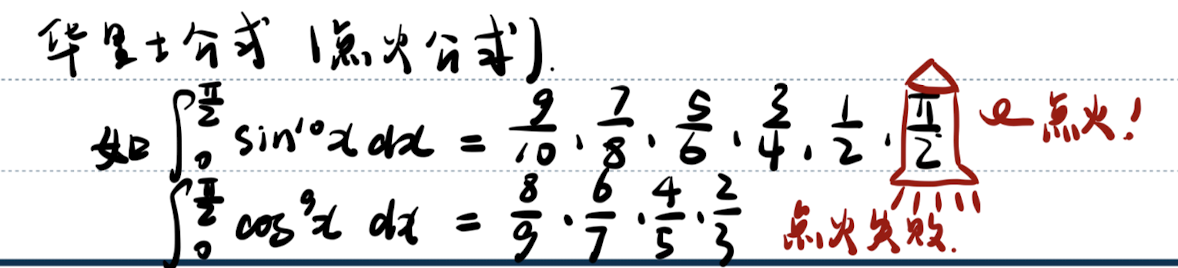
「记」二项式定理

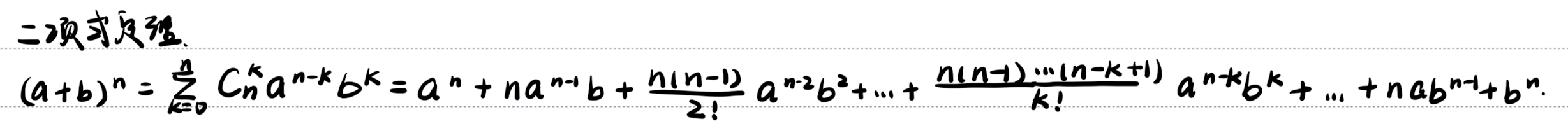
「记」常用基本不等式

（1）
（2）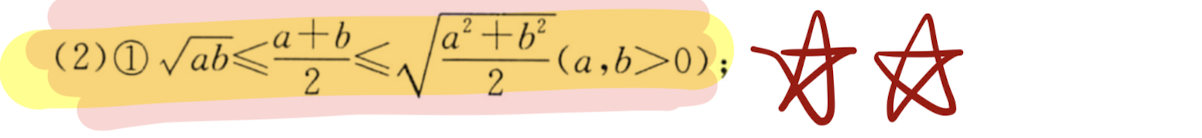
（3）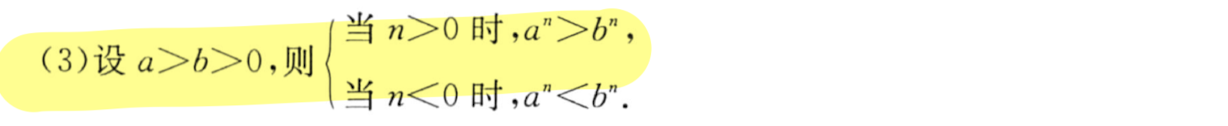
(4)
(5)
(6)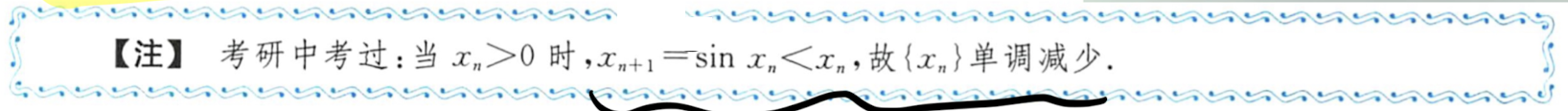
(7)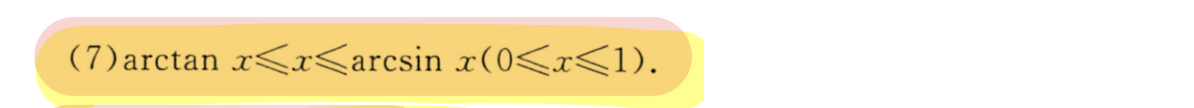
(8)
(9)
(10)

「记」函数极限的泰勒展开

「记」泰勒公式

「记」无穷小比阶

「记」常用等价无穷小

「记」两个重要极限

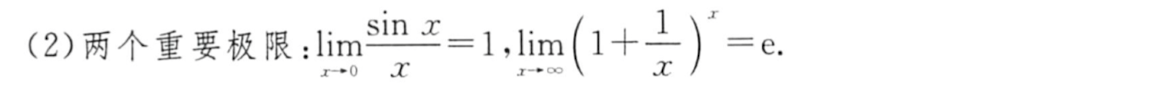
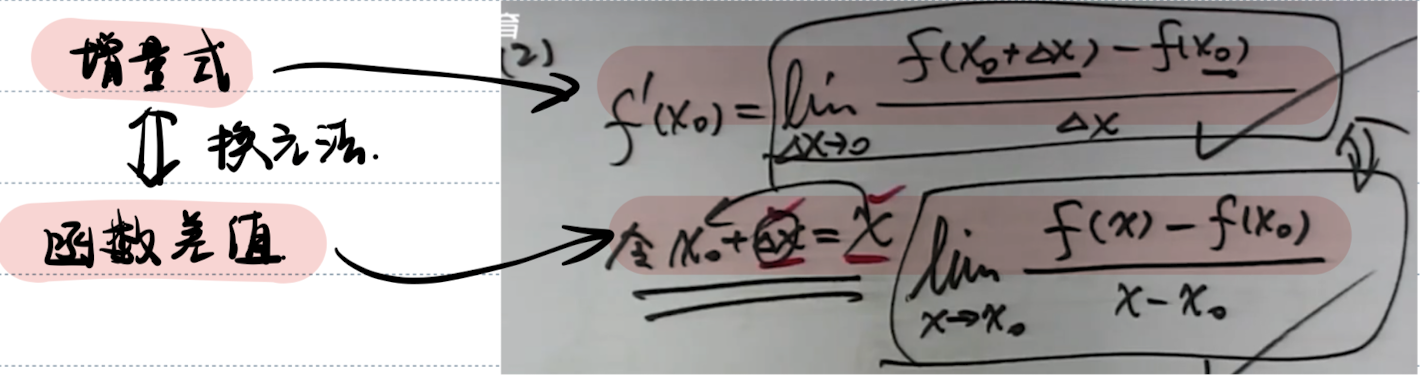
「记」导数定义的增量式及差值式

换元法

「记」变限积分求导公式

「记」变限积分求导三种情况

「记」高阶导数重要公式

「记」高阶求导莱布尼兹公式

「记」高阶导数泰勒公式

先写出 $y = f (x)$ 的泰勒公式或者麦克劳林公式，再通过比较系数来获得 $f^{(n)} (x_{0})$
具体来说，一般步骤如下

带拉格朗日余项的n阶泰勒公式

带佩亚诺余项的n阶泰勒公式

麦克劳林公式（特殊的泰勒公式）

麦克劳林展开式

「记」不定积分的基本积分公式

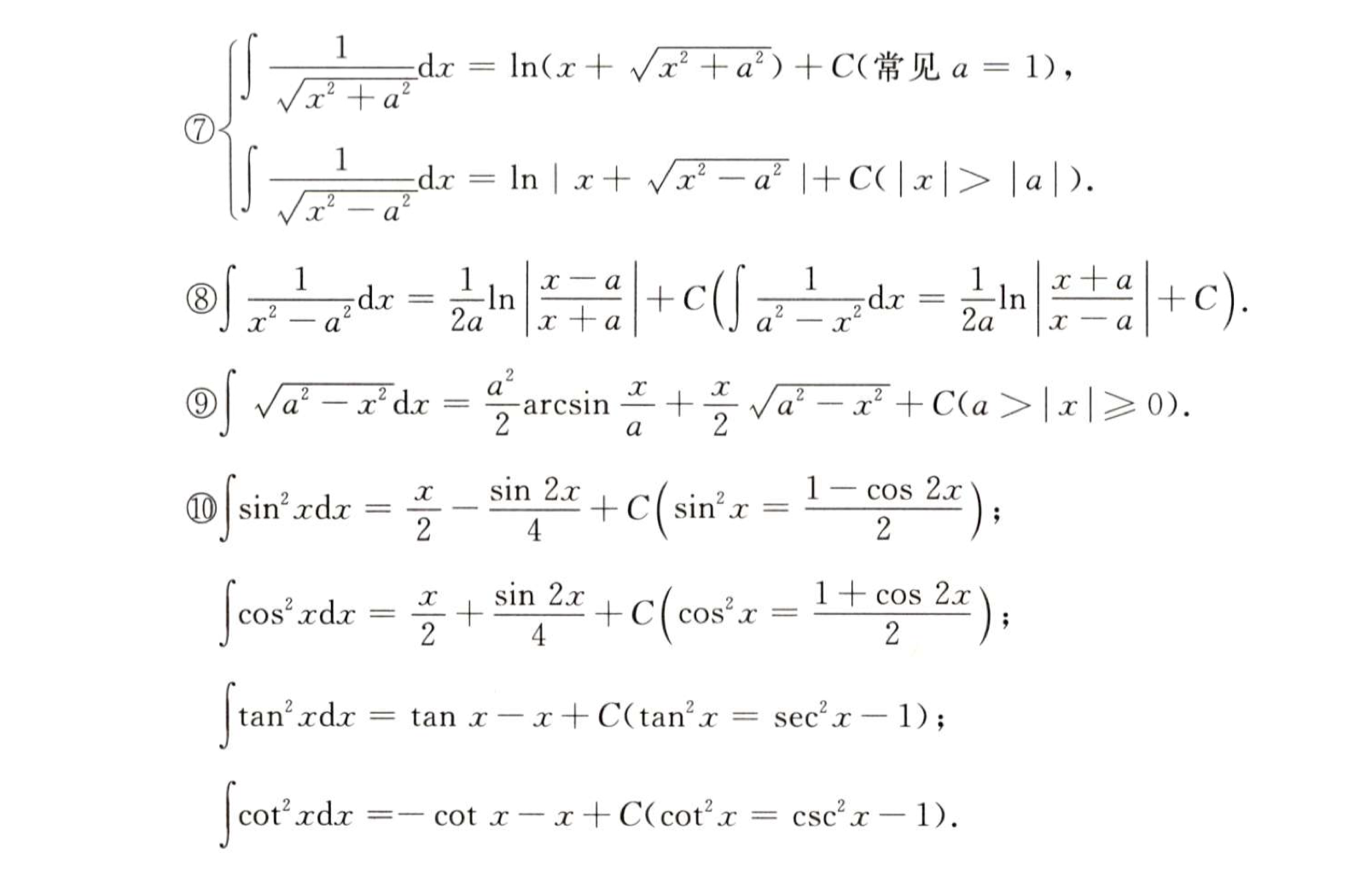
「记」有理函数的积分

「记」区间再现公式求解定积分

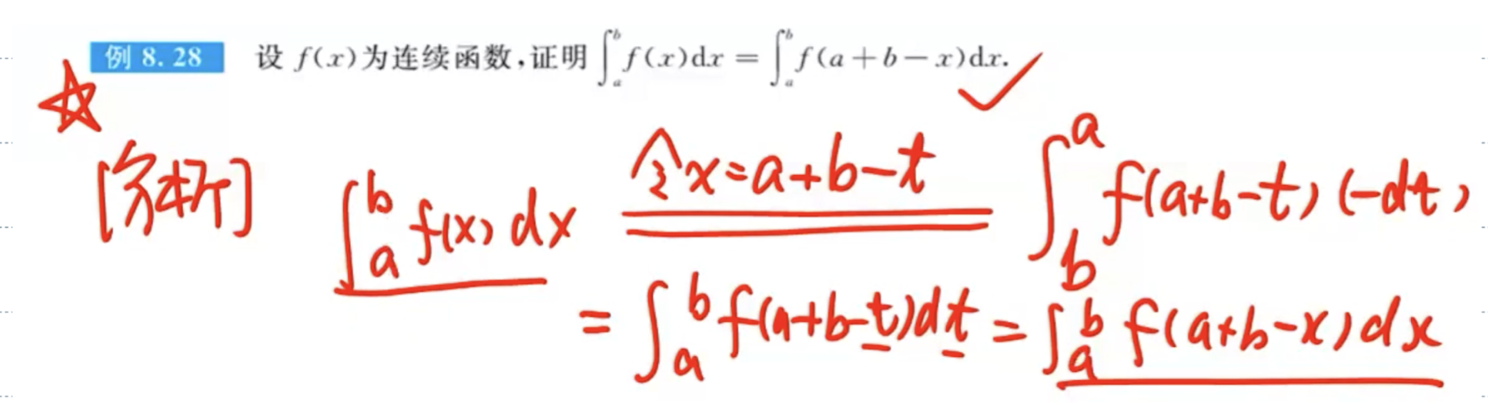
「记」华里士公式（点火公式）

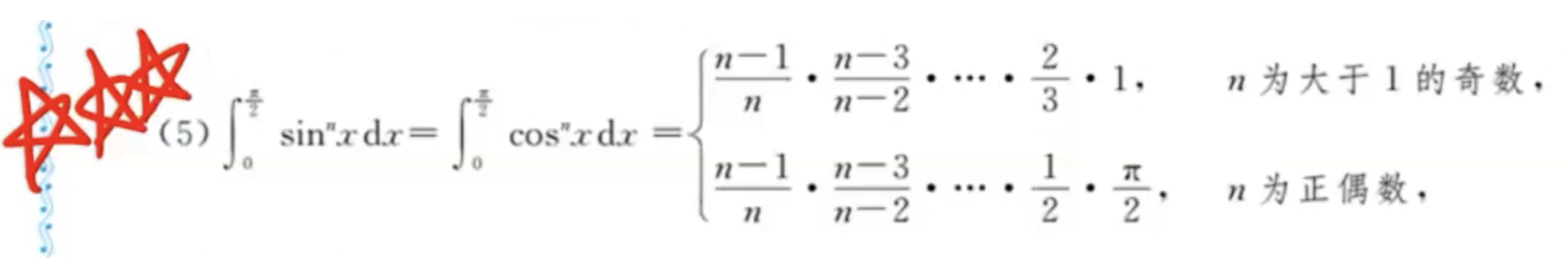
华里士公式求解高阶三角函数的定积分

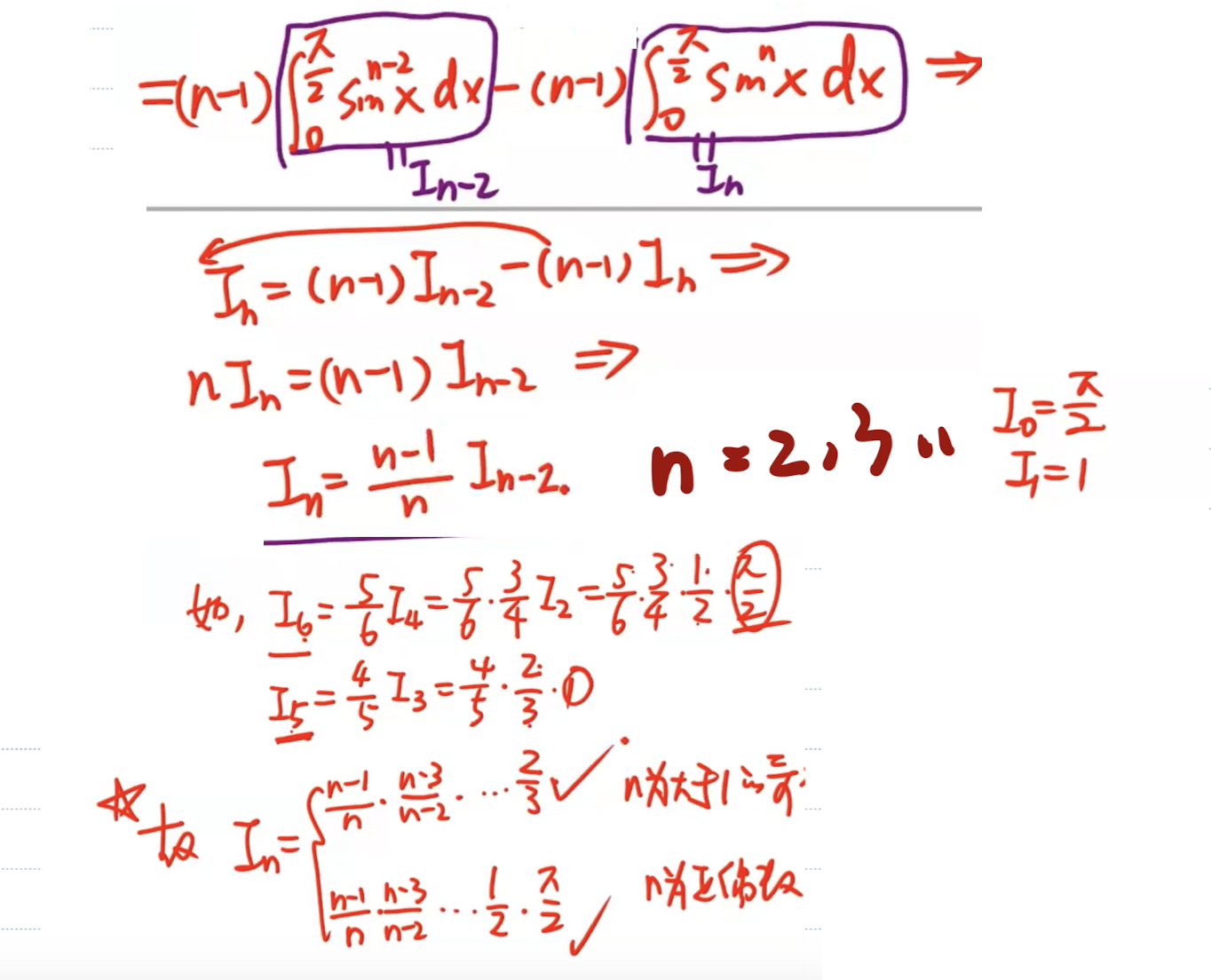
华里士公式变形、区间为(2, 2n）

$\sin^{n} x$ 以 $2 π$ 为周期

$\cos^{n} x$ 以 $2 π$ 为周期

华里士公式大全

点到直线距离公式

假设直线的方程为 $A x + B y + C = 0$ ，点的坐标为 $(x_{1}, y_{1})$
点 $(x_{1}, y_{1})$ 到直线 $A x + B y + C = 0$ 的距离 $d$ 可以表示为：

d = \frac{| A x_{1} + B y_{1} + C |}{\sqrt{A^{2} + B^{2}}}

A.公式汇总 ​

细碎知识点 ​

「记」双曲正弦、反双曲正弦、双曲余弦 ​

「记」幂函数相交面积 ​

「记」指数函数相交面积 ​

「记」快速计算三角函数面积 ​

「记」各三角函数之间的关系图 ​

「记」反三角函数计算总结 ​

「记」摆线方程 ​

「记」等差、等比、n项和数列公式 ​

「记」三角函数基本关系 ​

「记」三角函数重要公式 ​

「记」对数运算常考公式 ​

「记」一元二次方程基础 ​

「记」因式分解公式 ​

「记」阶乘与双阶乘 ​

「记」华里士公式（点火公式） ​

「记」二项式定理 ​

「记」常用基本不等式 ​

「记」函数极限的泰勒展开 ​

「记」泰勒公式 ​

「记」无穷小比阶 ​

「记」常用等价无穷小 ​

「记」两个重要极限 ​

「记」导数定义的增量式及差值式 ​

「记」变限积分求导公式 ​

「记」变限积分求导三种情况 ​

「记」高阶导数重要公式 ​

「记」高阶求导 莱布尼兹公式 ​

「记」高阶导数 泰勒公式 ​

带拉格朗日余项的n阶泰勒公式 ​

带佩亚诺余项的n阶泰勒公式 ​

麦克劳林公式（特殊的泰勒公式） ​

麦克劳林展开式 ​

「记」不定积分的基本积分公式 ​

「记」有理函数的积分 ​

「记」区间再现公式求解定积分 ​

「记」华里士公式（点火公式） ​

华里士公式求解高阶三角函数的定积分 ​

华里士公式变形、区间为(2, 2n） ​

华里士公式大全 ​

点到直线距离公式 ​

二重积分区域面积求法 ​

A.公式汇总

细碎知识点

「记」双曲正弦、反双曲正弦、双曲余弦

「记」幂函数相交面积

「记」指数函数相交面积

「记」快速计算三角函数面积

「记」各三角函数之间的关系图

「记」反三角函数计算总结

「记」摆线方程

「记」等差、等比、n项和数列公式

「记」三角函数基本关系

「记」三角函数重要公式

「记」对数运算常考公式

「记」一元二次方程基础

「记」因式分解公式

「记」阶乘与双阶乘

「记」华里士公式（点火公式）

「记」二项式定理

「记」常用基本不等式

「记」函数极限的泰勒展开

「记」泰勒公式

「记」无穷小比阶

「记」常用等价无穷小

「记」两个重要极限

「记」导数定义的增量式及差值式

「记」变限积分求导公式

「记」变限积分求导三种情况

「记」高阶导数重要公式

「记」高阶求导莱布尼兹公式

「记」高阶导数泰勒公式

带拉格朗日余项的n阶泰勒公式

带佩亚诺余项的n阶泰勒公式

麦克劳林公式（特殊的泰勒公式）

麦克劳林展开式

「记」不定积分的基本积分公式

「记」有理函数的积分

「记」区间再现公式求解定积分

「记」华里士公式（点火公式）

华里士公式求解高阶三角函数的定积分

华里士公式变形、区间为(2, 2n）

华里士公式大全

点到直线距离公式

二重积分区域面积求法