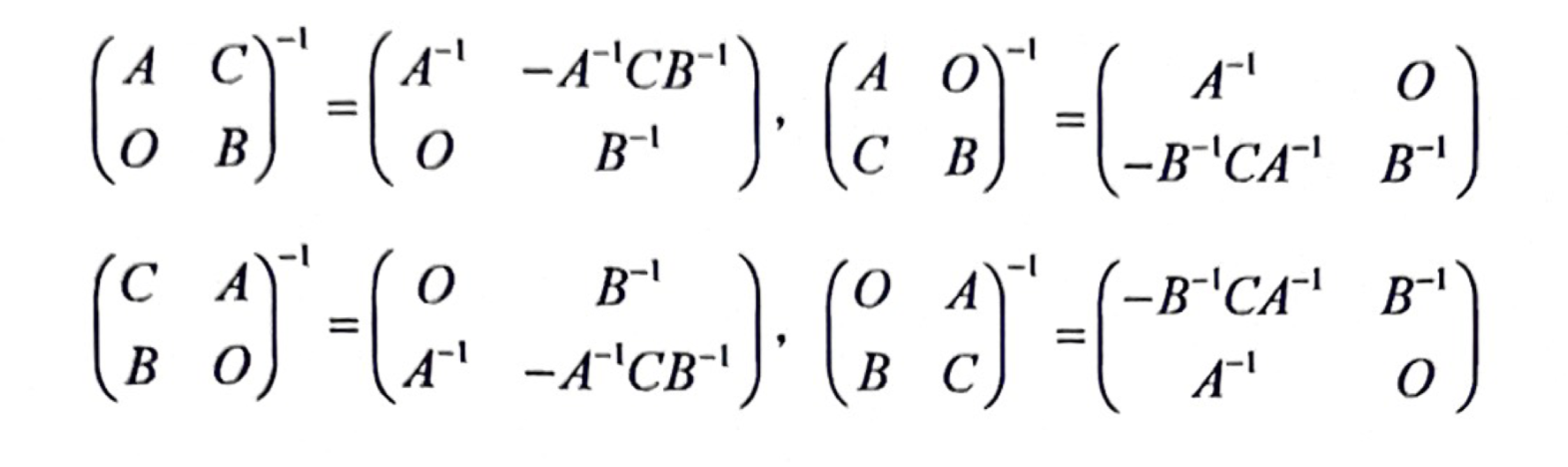第二章 矩阵
第一节 矩阵的基本运算
「矩阵」定义

「矩阵」加法的定义

「矩阵」数乘的定义

「矩阵」乘法的定义

「矩阵乘法」满足结合律和分配律
- 即
「矩阵乘法」不满足交换律
- 即在一般情况下

「矩阵乘法」不满足消去律
- 即在一般情况下
且 
「矩阵乘法」消去律的充分条件
「矩阵」转置的定义
- 矩阵 A 行列互换的得到的矩阵,成为 A 的转置矩阵,记作
「矩阵」转置的性质

「矩阵」对称、反对称矩阵的定义

第二节 矩阵的逆
「矩阵的逆」逆的定义

「矩阵的逆」逆的性质
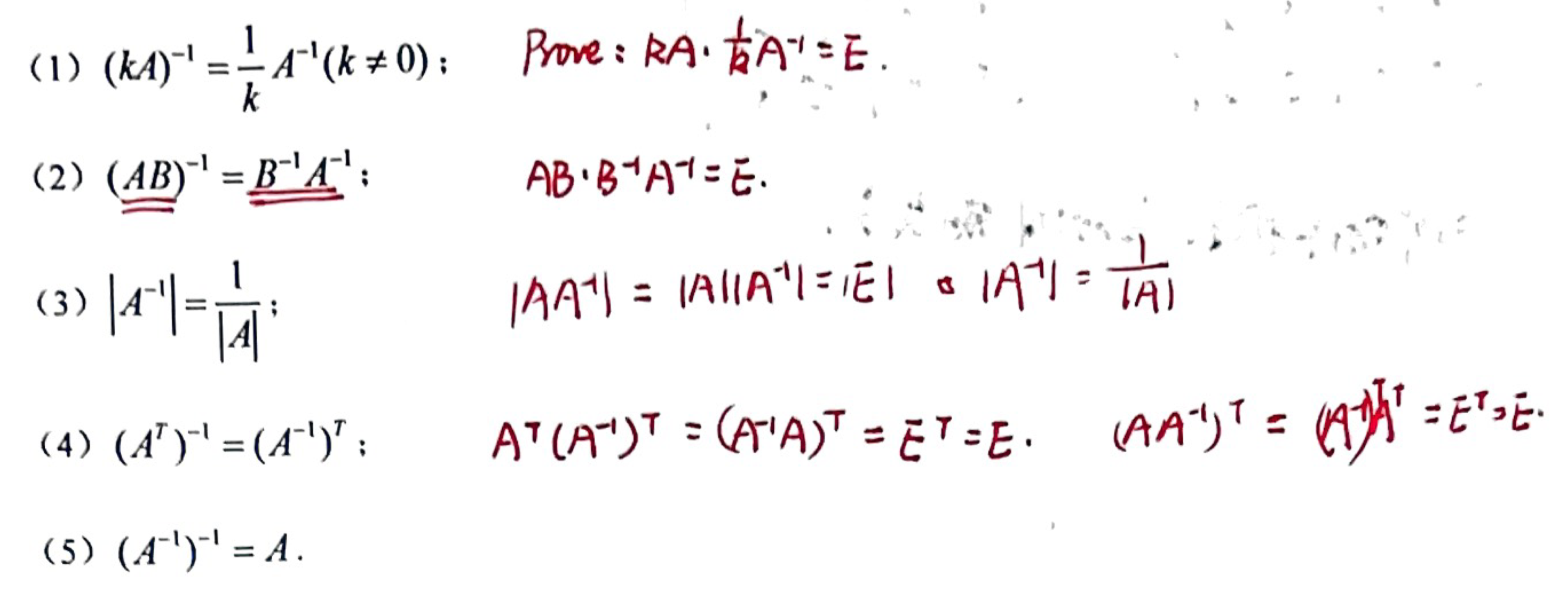
「矩阵的逆」可逆的充要条件

「矩阵的逆」逆的求法

第三节 矩阵的秩
「矩阵的秩」k阶子式的定义

「矩阵的秩」秩的定义

「矩阵的秩」二阶矩阵求逆
- 主对调,副变号
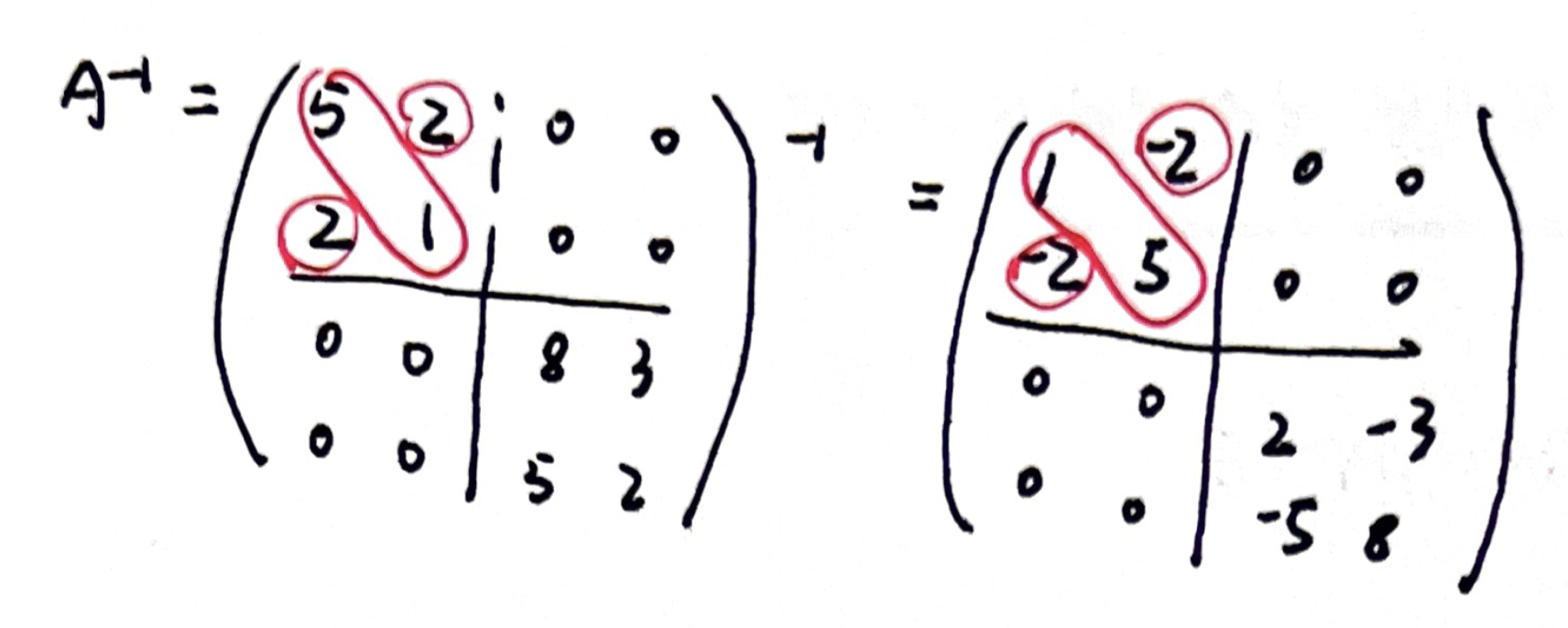
「矩阵的秩」满秩的定义


「矩阵的秩」秩的性质(9条)
- 口诀:单加积联常,逆满转积和

「矩阵的秩 & ⭐️」秩的求法
为数字矩阵 - 对
做初等行变换,化为行阶梯型矩阵,则 等于行阶梯型矩阵中非零行的行数 - 行阶梯型矩阵:每行第一位非 0 的数,下面的元素均为 0
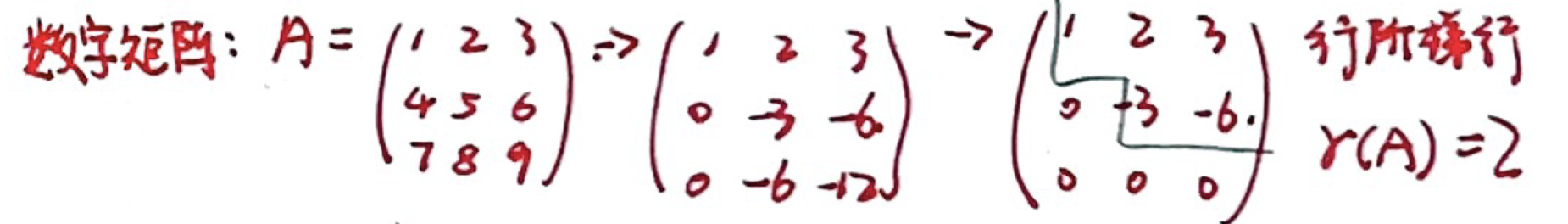
- 对
为抽象矩阵 - 利用秩的定义或性质
第四节 伴随矩阵
「伴随矩阵」定义
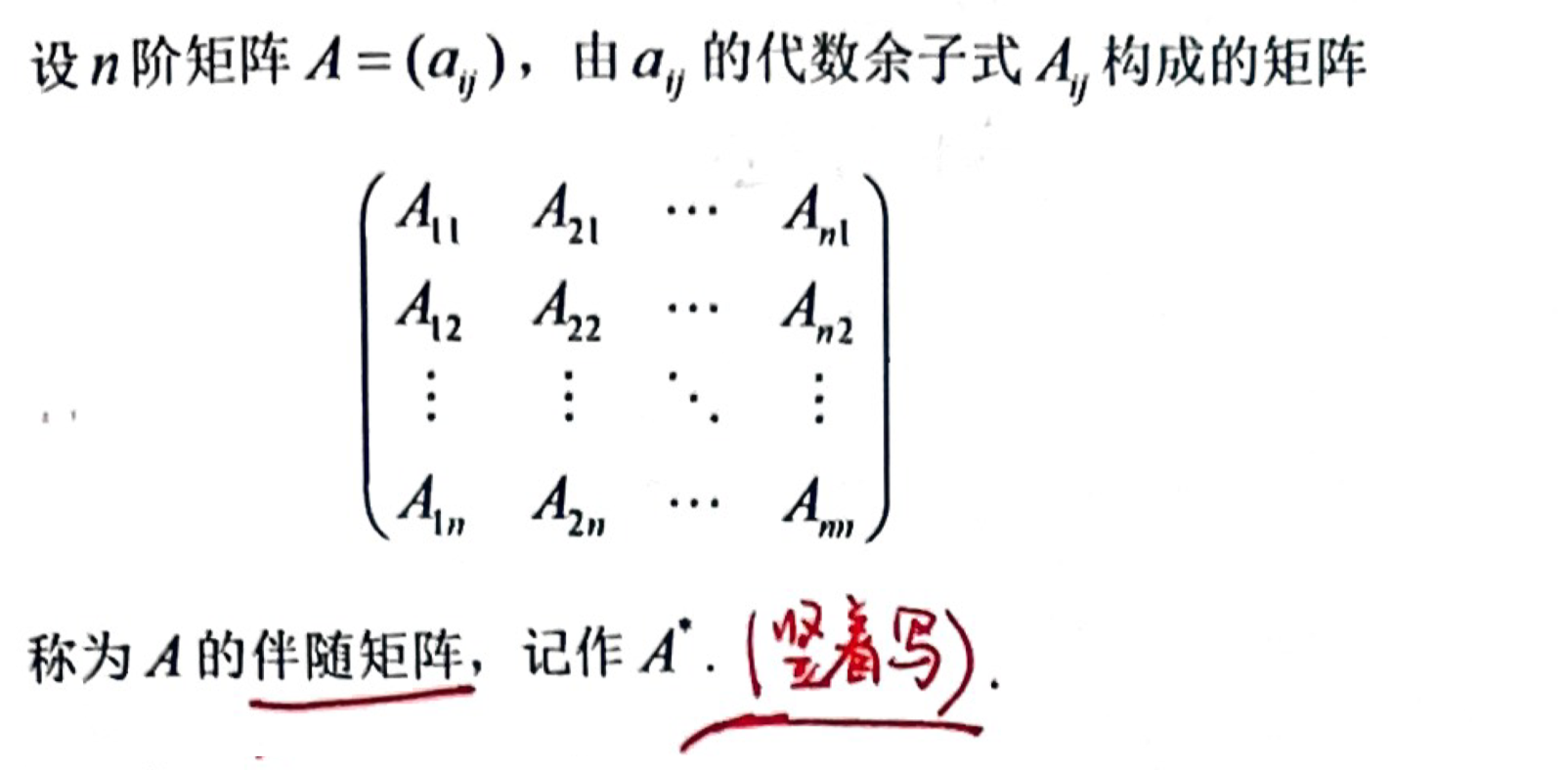
「伴随矩阵」性质


第五节 初等变换和初等矩阵
「初等变换和初等矩阵」初等变换的定义

「初等变化和初等矩阵」初等矩阵的定义
- 单位矩阵
经过一次初等变化所得到的矩阵为初等矩阵 
「初等变化和初等矩阵」性质

「初等变化和初等矩阵」应用

「矩阵等价」定义
- 若矩阵 A 可以经过有限次初等变换变为矩阵 B,则称 A 与 B 等价,记作
「矩阵等价」充要条件

第六节 分块矩阵
「分块矩阵」加法
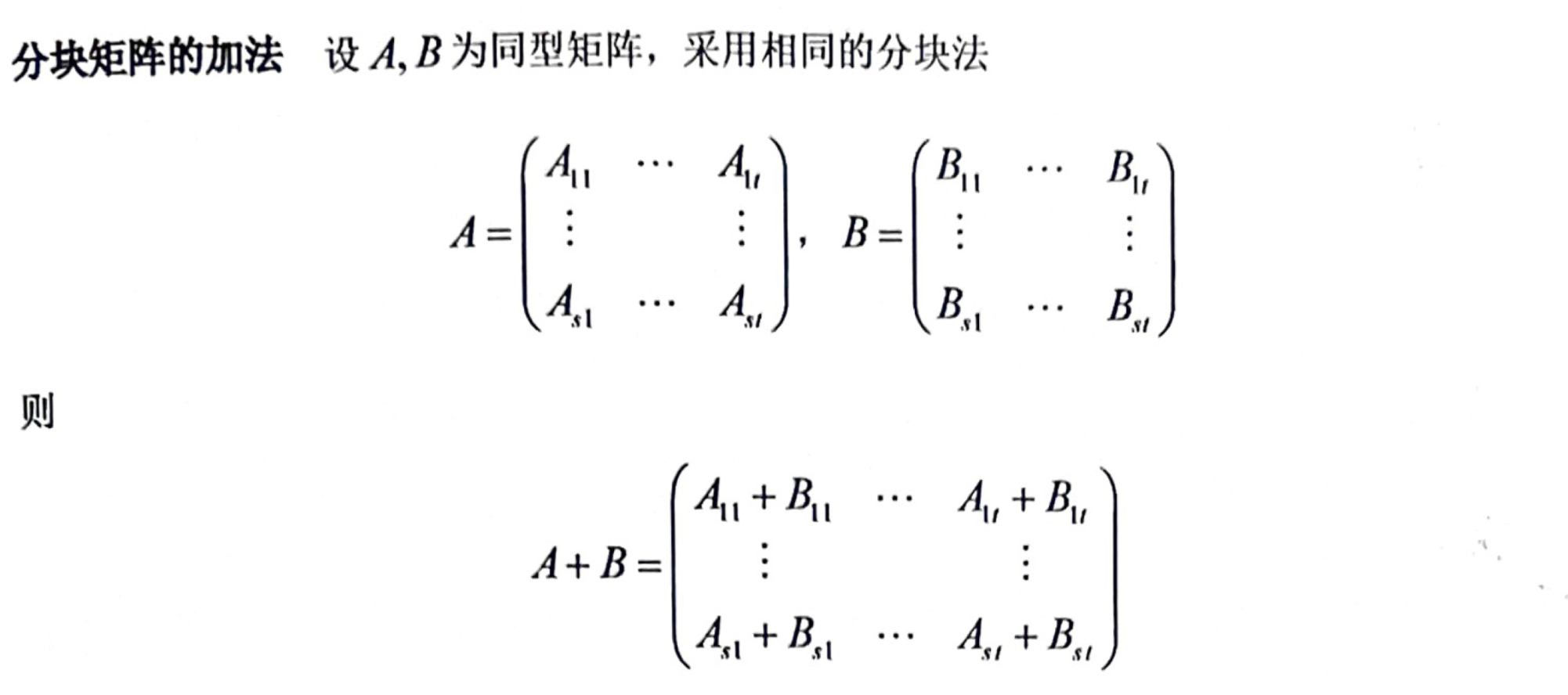
「分块矩阵」数乘

「分块矩阵」乘法


「分块矩阵」转置
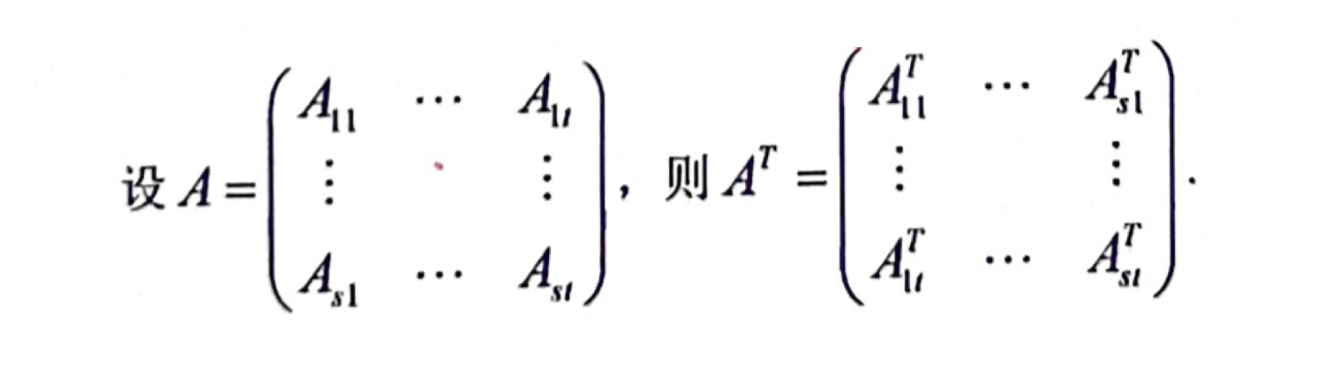
「分块矩阵」逆

「分块矩阵」逆的推广(150)