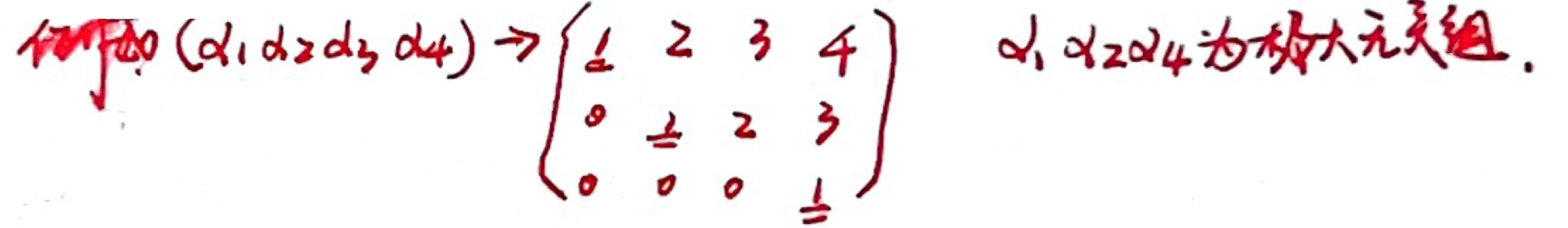第三章向量

第一节向量的基本运算

「向量」定义

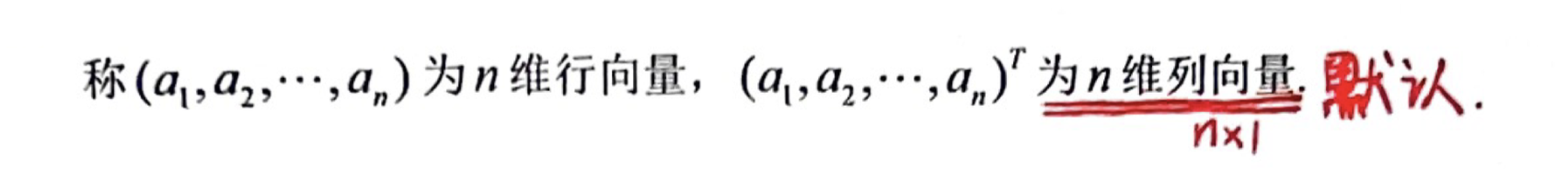
「向量」加法的定义

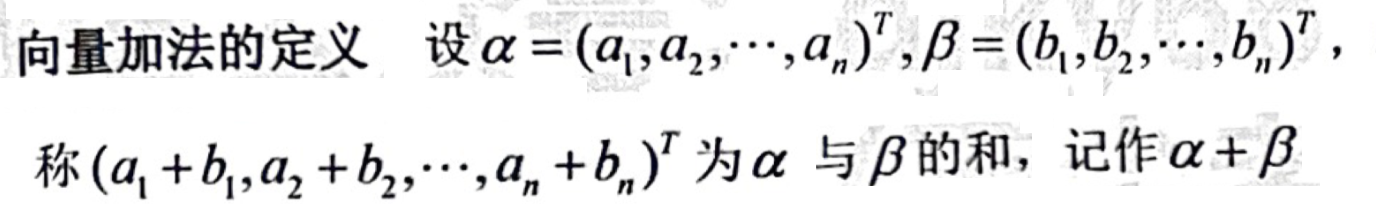
「向量」数乘的定义

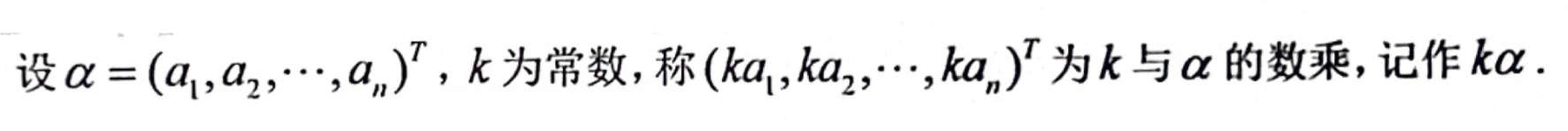
「向量」内积（数量积）的定义

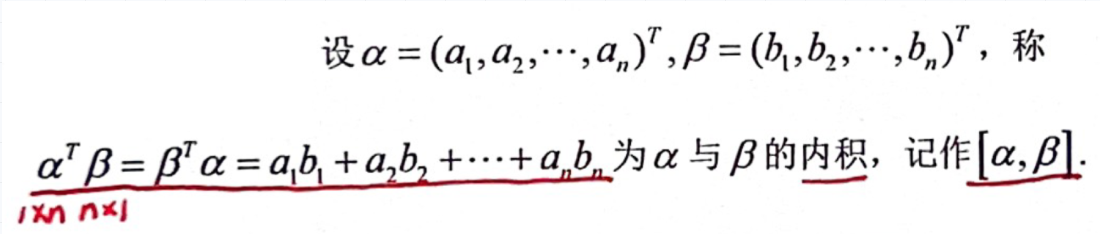
若 $[α, β] = 0$ ， $α$ 与 $β$ 正交，显然零向量与任意向量均正交。

「向量」长度的定义

「正交矩阵」定义

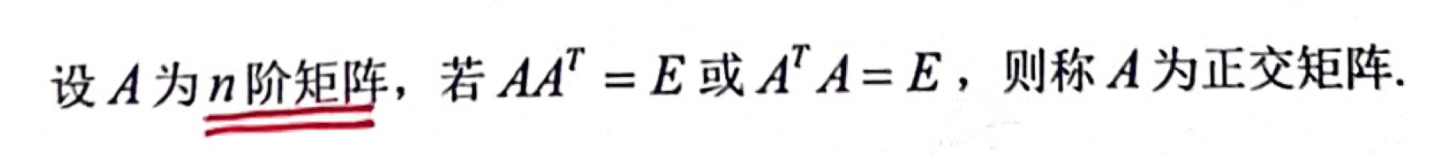
「正交矩阵」充要条件

「正交矩阵」性质

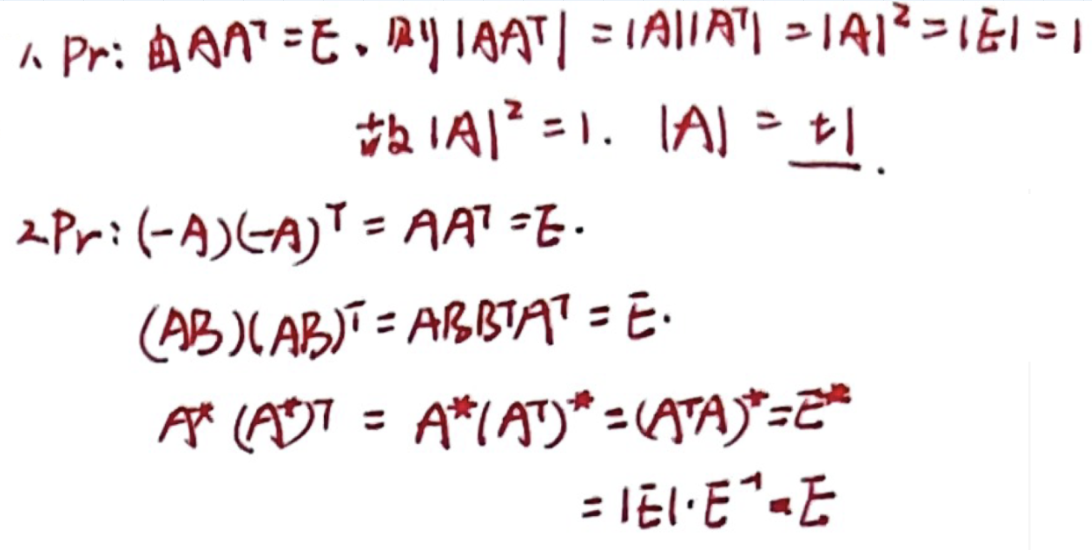
「正交矩阵」Schmidt 正交化定义

ex1

第二节线性表示

「线性表示」线性组合的定义

「线性表示」定义

「线性表示」向量组等价的定义

向量组之间的线性表示

向量组之间的等价

ex1

「线性表示」充要条件

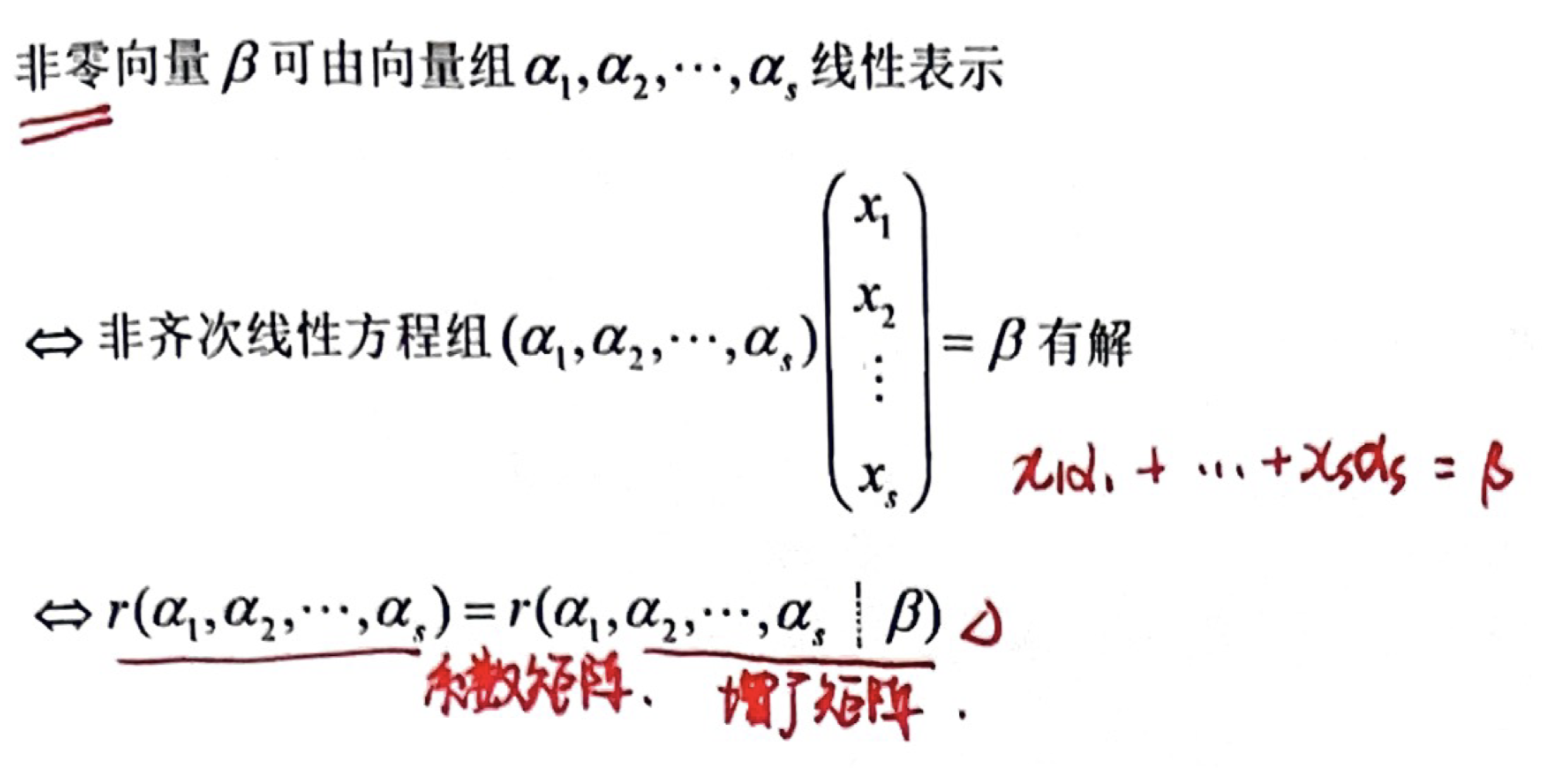
「线性表示」向量组等价的充要条件

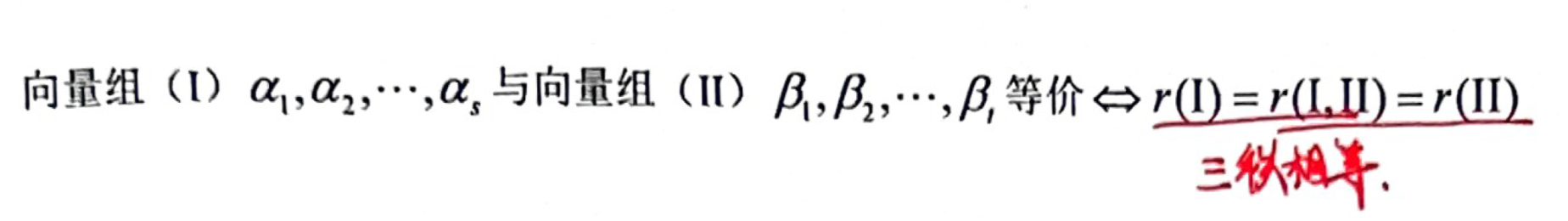
「线性表示」充分条件

「线性表示」求法

行最简形矩阵
- 每行第一个非零的数均为 1，1的上方下方均为 0

第三节线性相关和线性无关

「线性相关、无关」定义

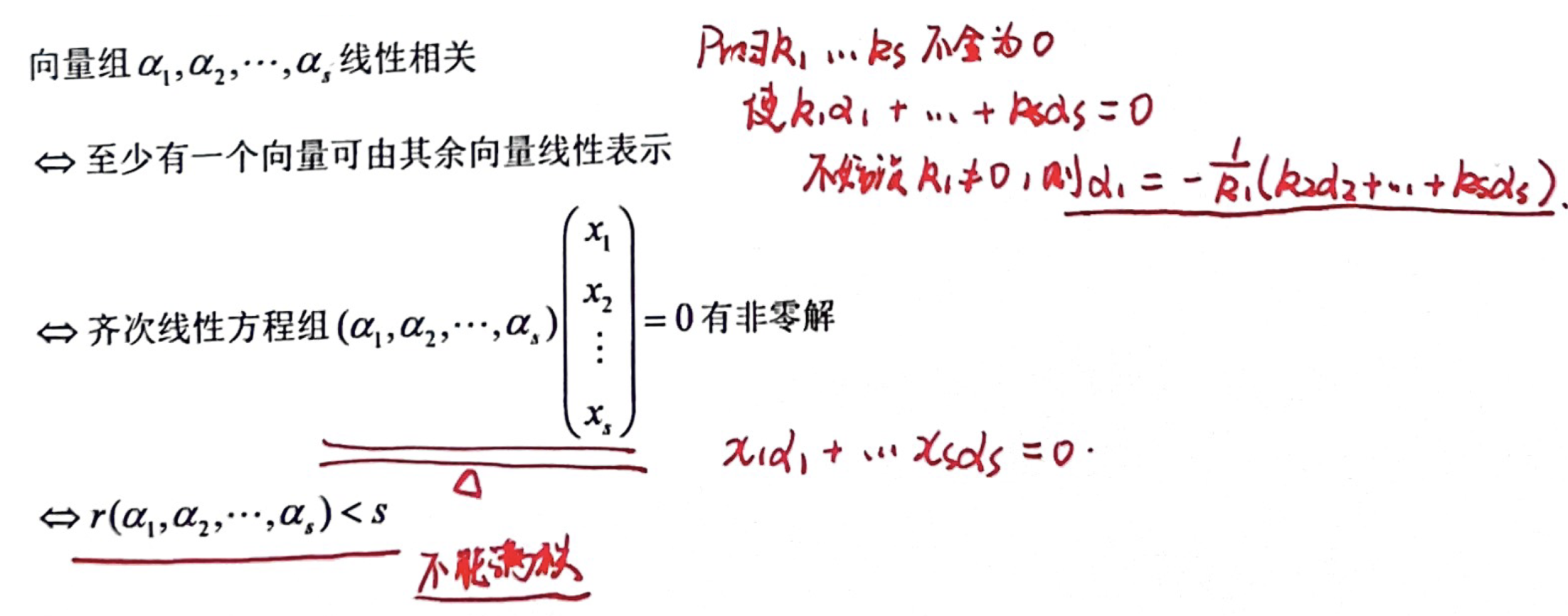
「线性相关、无关」线性相关的充要条件

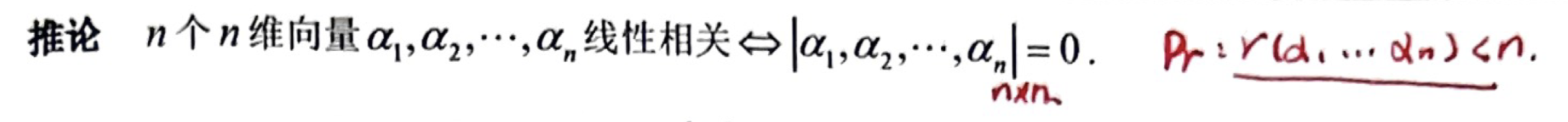
「线性相关、无关」线性相关的充分条件

含有零向量的向量组线性相关
部分相关，则整体相关
高维相关，则地位相关
（⭐️）设向量组 $α_{1}, α_{2}, \cdot \cdot \cdot, α_{s}$ 线性无关，可由向量组 $β_{1}, β_{2}, \cdot \cdot \cdot, β_{s}$ 线性表示，且 $s > t$ ，则 $α_{1}, α_{2}, \cdot \cdot \cdot, α_{s}$ 线性相关，即以少表多，多必相关。
逆否命题
- 设向量组 $α_{1}, α_{2}, \cdot \cdot \cdot, α_{s}$ 线性无关，可由向量组 $β_{1}, β_{2}, \cdot \cdot \cdot, β_{s}$ 线性表示，且 $s \leq t$ ，则 $α_{1}, α_{2}, \cdot \cdot \cdot, α_{s}$ 线性相关，即无关被表，个数不多。

证明过程

推论
- $n + 1$ 个 $n$ 维向量（即向量维数小于向量个数）线性相关

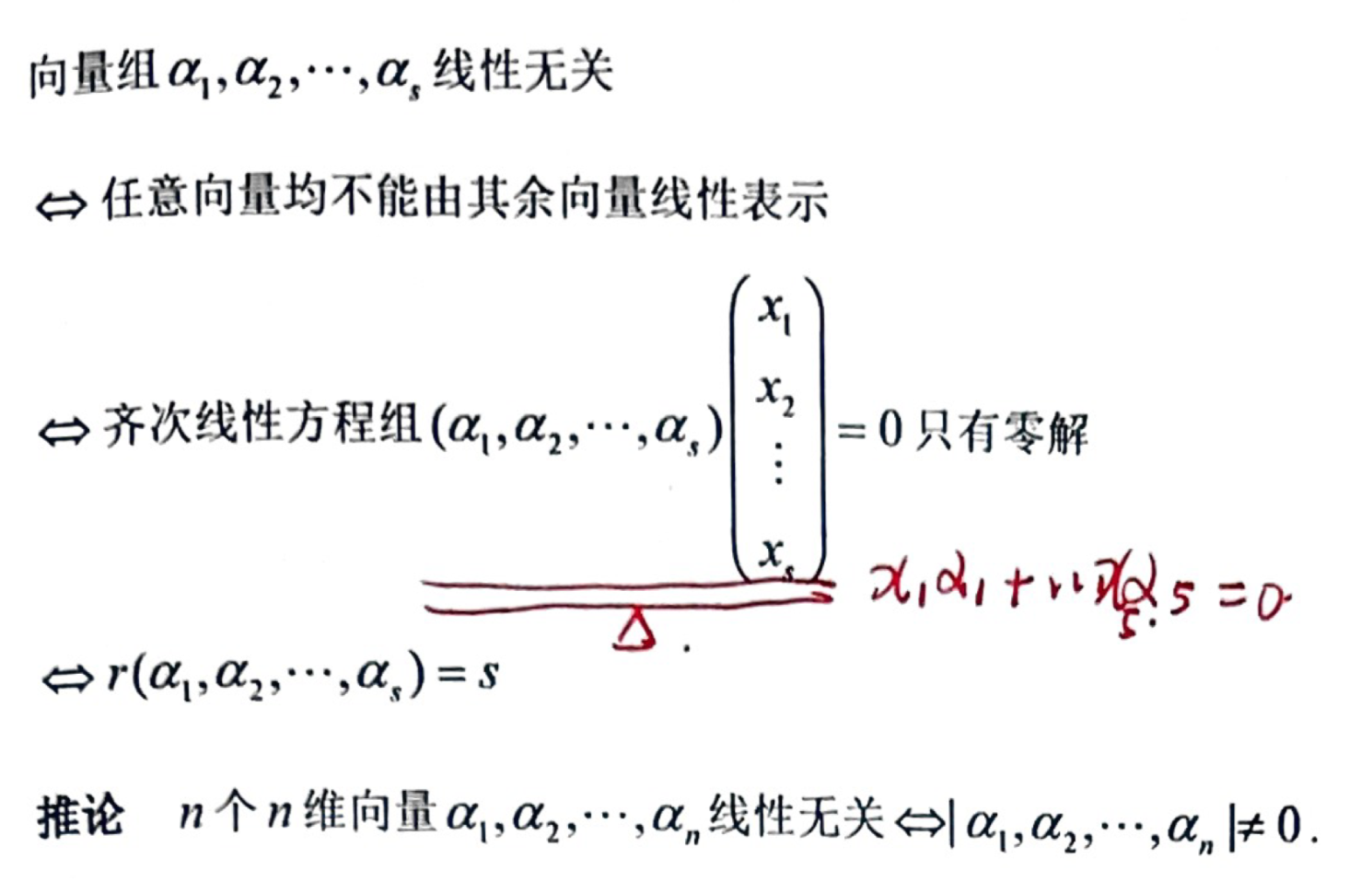
「线性相关、无关」线性无关的充要条件

「线性相关、无关」线性相关的充分条件

整体无关，则低维无关
低维无关，则高维无关
不含零向量的正交向量组线性无关
不同特征值的特征向量线性无关

(1)、(2) 为线性相关的逆否命题

(3) 证明过程

第四节极大线性无关组和向量组的秩

「极大线性无关组」定义

设向量组 $α_{1}, α_{2}, \cdot \cdot \cdot, α_{s}$ 中存在 $r$ 个向量 $α_{i_{1}}, α_{i_{2}}, \cdot \cdot \cdot, α_{i_{s}}$ 线性无关，再加入其余任意向量就线性相关（其余向量均可由其线性表示），则称 $α_{i_{1}}, α_{i_{2}}, \cdot \cdot \cdot, α_{i_{s}}$ 为 $α_{1}, α_{2}, \cdot \cdot \cdot, α_{s}$ 的极大线性无关组。

「极大线性无关组」向量组的秩的定义

极大线性无关组中向量的个数称为向量组的秩
评注
1. 极大线性无关组不唯一，若向量组的秩为 r，则任意 r 个线性无关的向量均为极大线性无关组。
2. （⭐️）矩阵的秩等于其列向量组的秩，也等于其行向量组的秩。
- （评注 2 举例）

「极大线性无关组」求法

对 $α_{1}, α_{2}, \cdot \cdot \cdot, α_{s}$ 作初等行变换，化为行阶梯形矩阵，则行阶梯型矩阵中每行第一个非零元素对应的列向量构成极大线性无关组。

A111.高等数学

A112.线性代数

A113.概率论与数理统计

A212.C++

A214.Swift

A221.数据结构

A222.计算机组成原理

A223.计算机操作系统

A224.计算机网络

1231.常见算法

第三章向量

第一节向量的基本运算

「向量」定义

「向量」加法的定义

「向量」数乘的定义

「向量」内积（数量积）的定义

「向量」长度的定义

「正交矩阵」定义

「正交矩阵」充要条件

「正交矩阵」性质

「正交矩阵」Schmidt 正交化定义

第二节线性表示

「线性表示」线性组合的定义

「线性表示」定义

「线性表示」向量组等价的定义

「线性表示」充要条件

「线性表示」向量组等价的充要条件

「线性表示」充分条件

「线性表示」求法

第三节线性相关和线性无关

「线性相关、无关」定义

「线性相关、无关」线性相关的充要条件

「线性相关、无关」线性相关的充分条件

「线性相关、无关」线性无关的充要条件

「线性相关、无关」线性相关的充分条件

第四节极大线性无关组和向量组的秩

「极大线性无关组」定义

「极大线性无关组」向量组的秩的定义

「极大线性无关组」求法

第三章 向量 ​

第一节 向量的基本运算 ​

「向量」定义 ​

「向量」加法的定义 ​

「向量」数乘的定义 ​

「向量」内积（数量积）的定义 ​

「向量」长度的定义 ​

「正交矩阵」定义 ​

「正交矩阵」充要条件 ​

「正交矩阵」性质 ​

「正交矩阵」Schmidt 正交化定义 ​

第二节 线性表示 ​

「线性表示」线性组合的定义 ​

「线性表示」定义 ​

「线性表示」向量组等价的定义 ​

「线性表示」充要条件 ​

「线性表示」向量组等价的充要条件 ​

「线性表示」充分条件 ​

「线性表示」求法 ​

第三节 线性相关和线性无关 ​

「线性相关、无关」定义 ​

「线性相关、无关」线性相关的充要条件 ​

「线性相关、无关」线性相关的充分条件 ​

「线性相关、无关」线性无关的充要条件 ​

「线性相关、无关」线性相关的充分条件 ​

第四节 极大线性无关组和向量组的秩 ​

「极大线性无关组」定义 ​

「极大线性无关组」向量组的秩的定义 ​

「极大线性无关组」求法 ​

第三章向量

第一节向量的基本运算

「向量」定义

「向量」加法的定义

「向量」数乘的定义

「向量」内积（数量积）的定义

「向量」长度的定义

「正交矩阵」定义

「正交矩阵」充要条件

「正交矩阵」性质

「正交矩阵」Schmidt 正交化定义

第二节线性表示

「线性表示」线性组合的定义

「线性表示」定义

「线性表示」向量组等价的定义

「线性表示」充要条件

「线性表示」向量组等价的充要条件

「线性表示」充分条件

「线性表示」求法

第三节线性相关和线性无关

「线性相关、无关」定义

「线性相关、无关」线性相关的充要条件

「线性相关、无关」线性相关的充分条件

「线性相关、无关」线性无关的充要条件

「线性相关、无关」线性相关的充分条件

第四节极大线性无关组和向量组的秩

「极大线性无关组」定义

「极大线性无关组」向量组的秩的定义

「极大线性无关组」求法