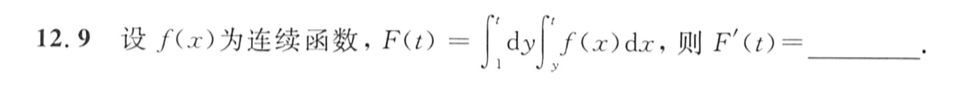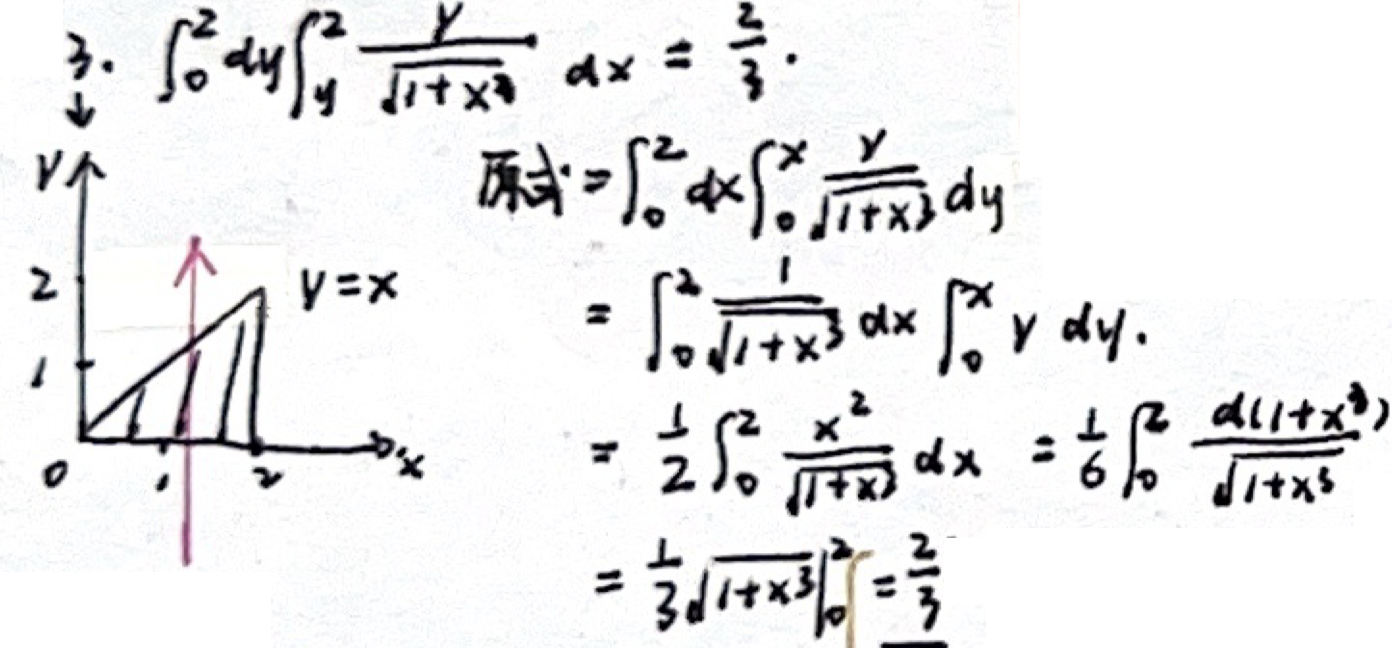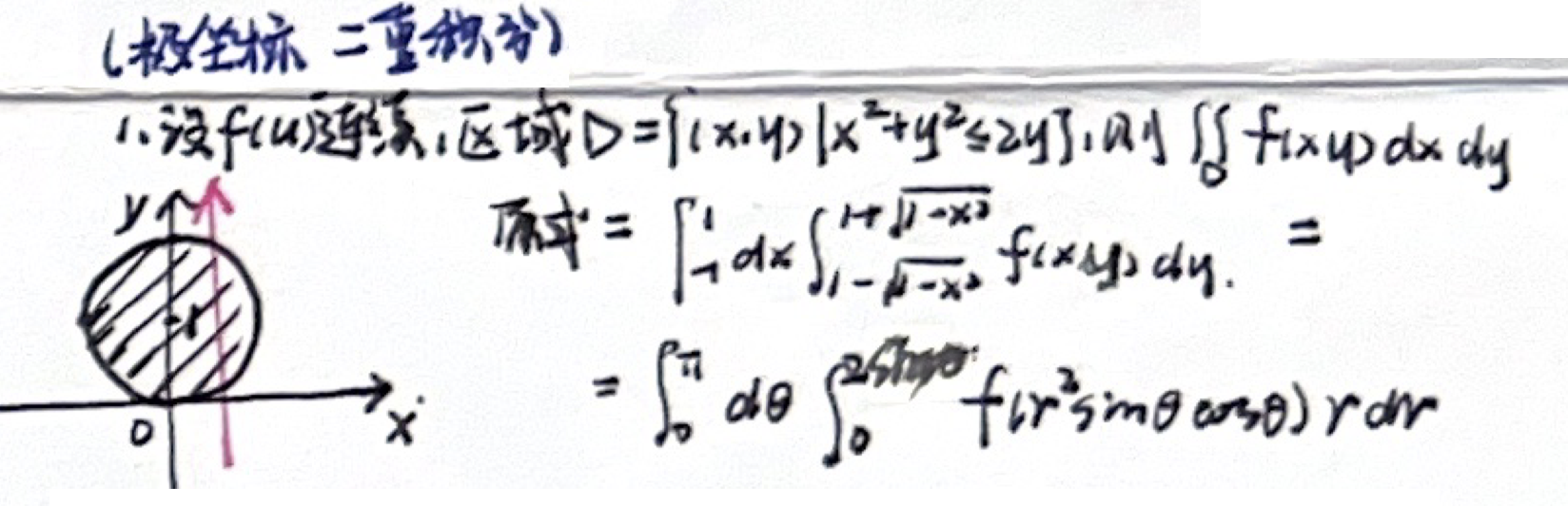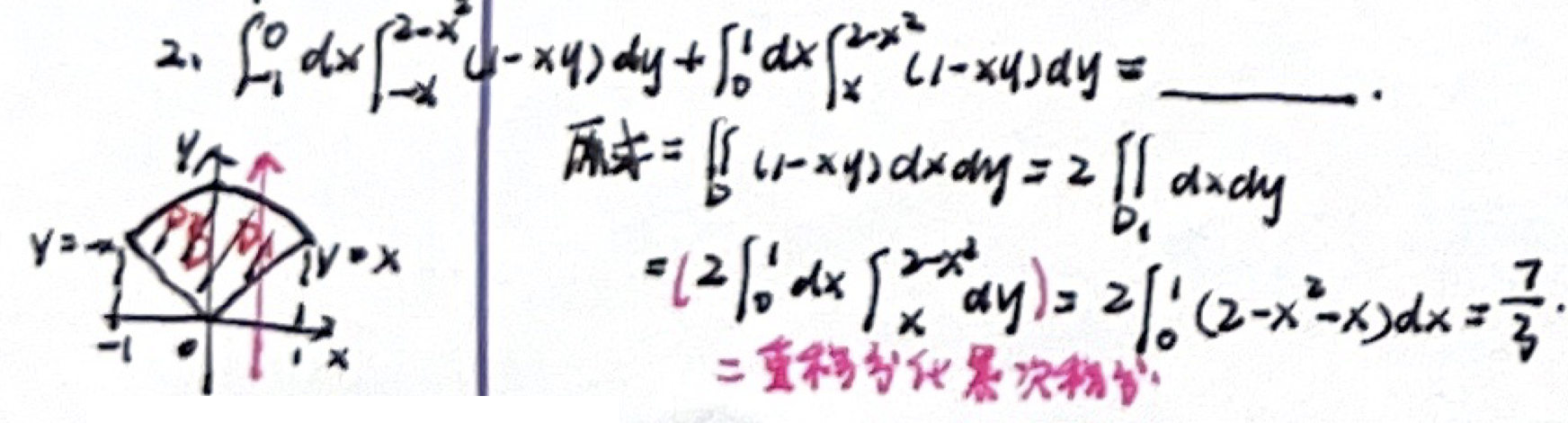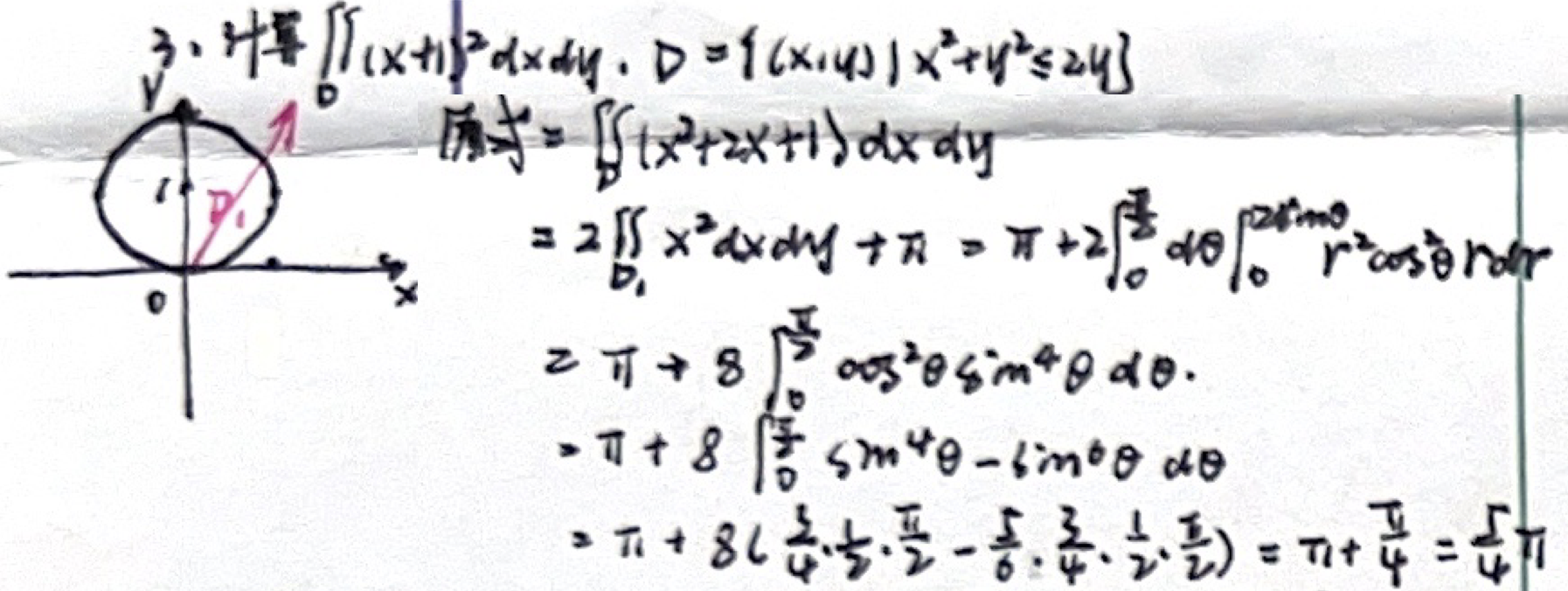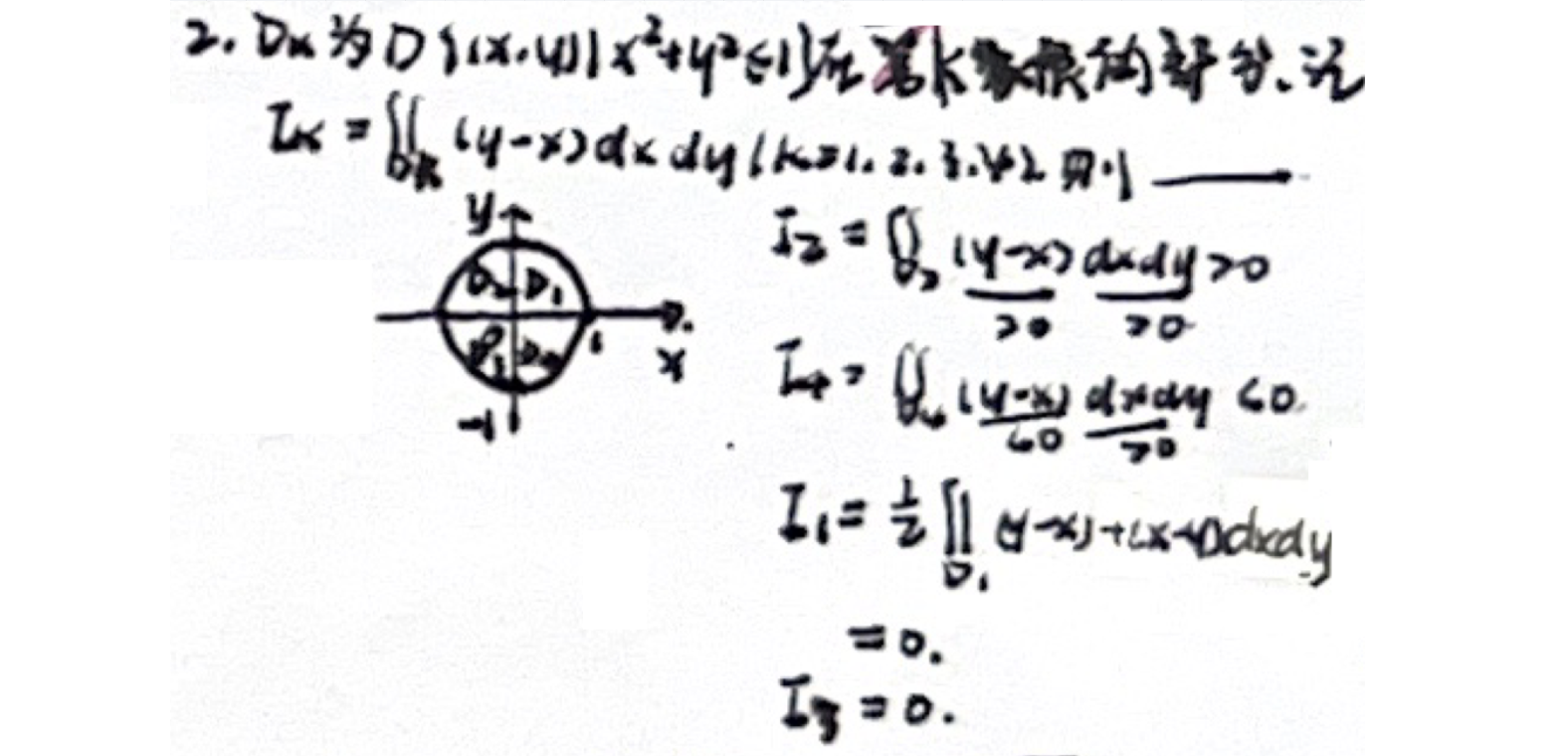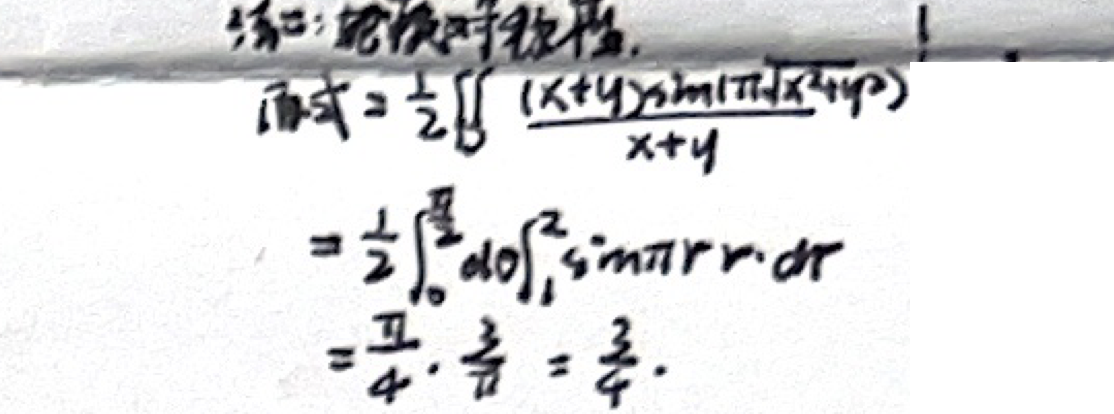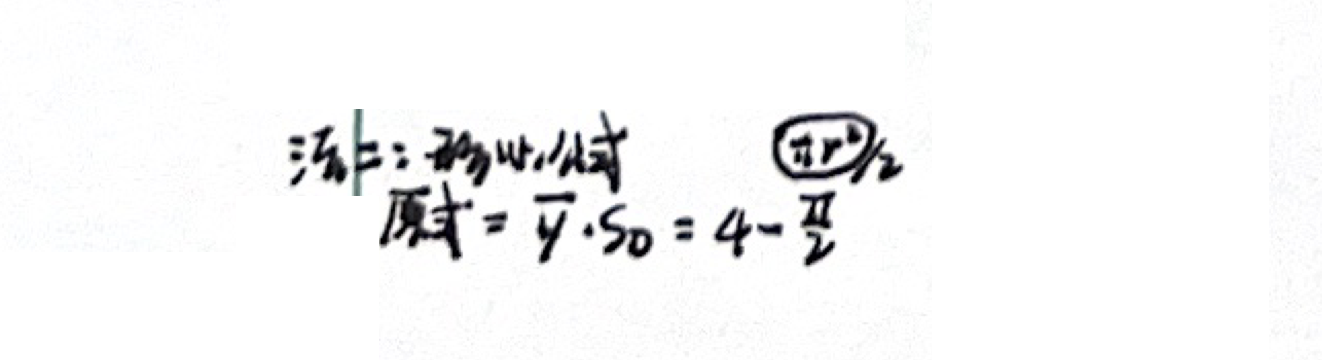第十七节二重积分

「二重积分」定义

$lim_{λ \to 0} \sum_{i = 1}^{n} f (ξ_{i}, η_{i}) Δ σ_{i}$ 是 求和的极限

「二重积分」几何意义（曲顶柱体的体积）

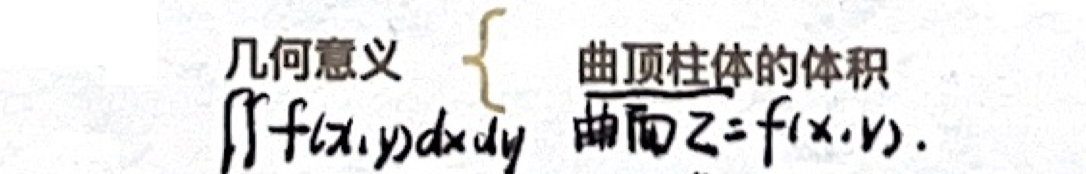
「二重积分」不等式性质

若 D 上 $f (x, y) \leq g (x, y)$ ，则 $\iint_{D} f (x, y) d σ \leq \iint_{D} g (x, y) d σ$
$\iint_{D} (k_{1} f_{1} + k_{2} f_{2}) d x d y = k_{1} \iint_{D} f_{1} d x d y + k_{2} \iint_{D} f_{2} d x d y$ （线性）
积分的绝对值不超过绝对值的积分
- $| \iint_{D} f (x, y) d σ | \leq \iint_{D} | f (x, y) | d σ$

「二重积分」中值定理性质

若 $f (x, y)$ 在闭区域 D 连续，则存在 $(ξ, η) \in D$ ，使得
- $\iint_{D} f (x, y) d x d y = f (ξ, η) S_{D}$

「二重积分」区间可加性

闭区域被分成两个闭区域 $D_{1}, D_{2}$ ，则
- $\iint_{D} f (x, y) d x d y = \iint_{D_{1}} f (x, y) d x d y + \iint_{D_{2}} f (x, y) d x d y$

「二重积分」估值定理

若 $f (x, y)$ 在闭区域 $D$ 连续，最大值为 $M$ ，最小值为 $m$ ，则
- $m S_{D} \leq [] \leq \iint_{D} M d x d y = M \cdot S_{D}$
- $m \cdot S_{D} \leq \iint_{D} f (x, y) d x d y \leq M \cdot S_{D}$

「直角坐标计算」先 Y 后 X（X型区域）

「直角坐标计算」先 X 后 Y（Y型区域）

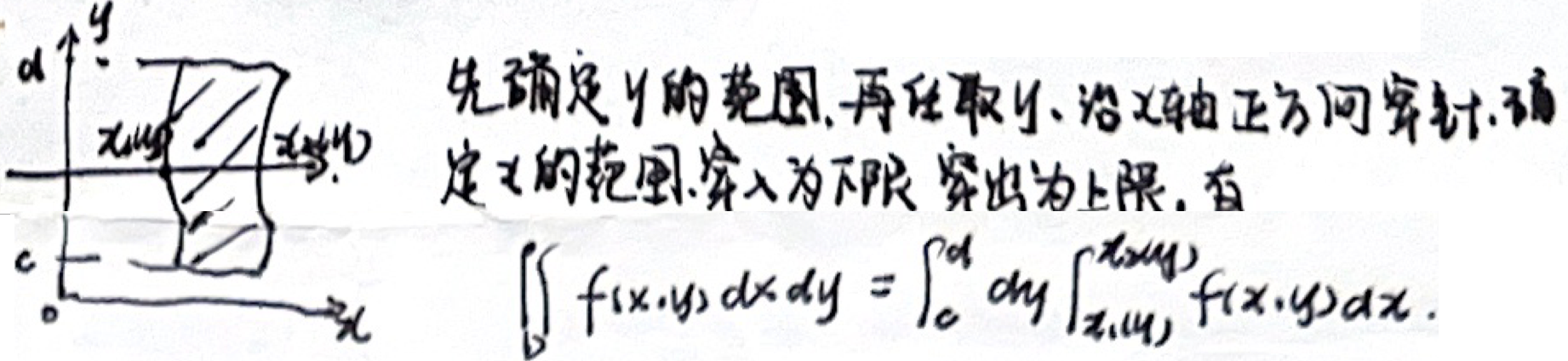
「极坐标计算」被积函数

被积函数为 $f (x^{2} + y^{2})$ 或 $D$ 为圆域
先 $ρ$ 后 $θ$
$f (\sqrt{x^{2} + y^{2}}), f (\frac{y}{x}), f (\frac{x}{y})$

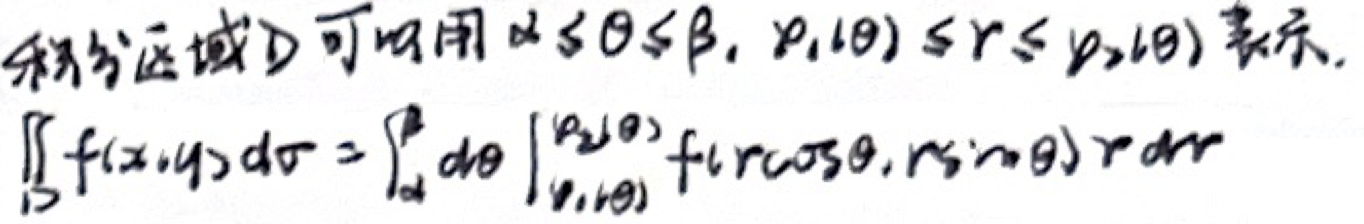
「极坐标计算」积分域

被积函数为 $f (x^{2} + y^{2})$ 或 $D$ 为圆域
先 $ρ$ 后 $θ$

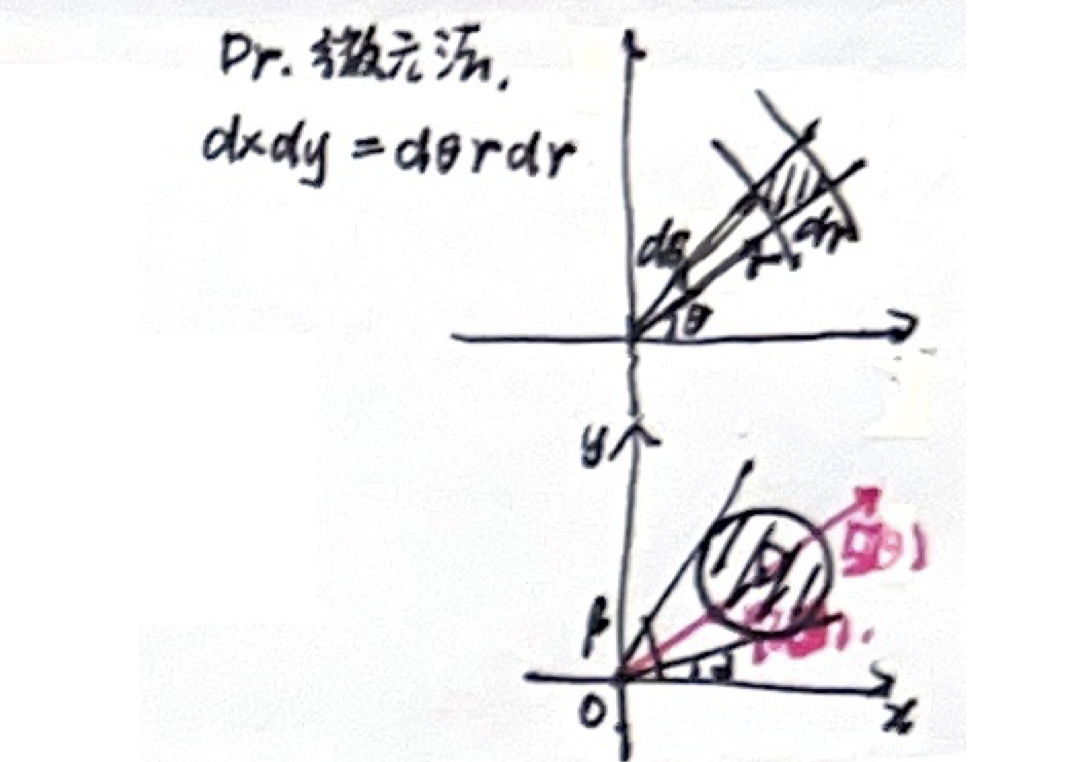
「直角坐标和极坐标的相互转化」微元法

被积函数为 $f (x^{2} + y^{2})$ 或 $D$ 为圆域
先 $ρ$ 后 $θ$

「奇偶性」（出必用）

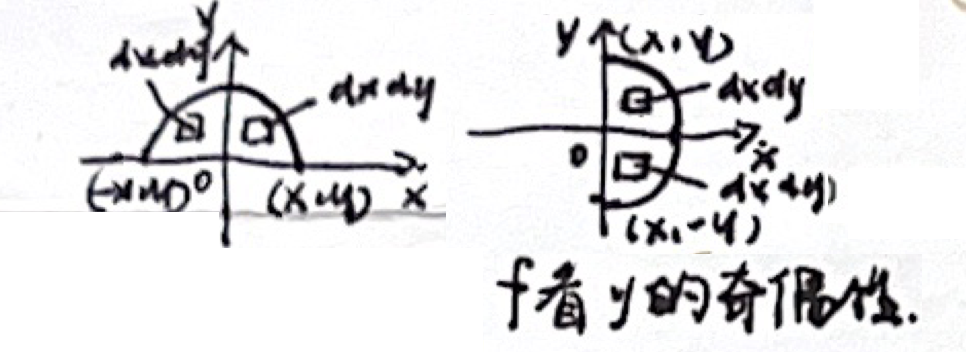
「奇偶性」积分域 D 关于 y 轴对称

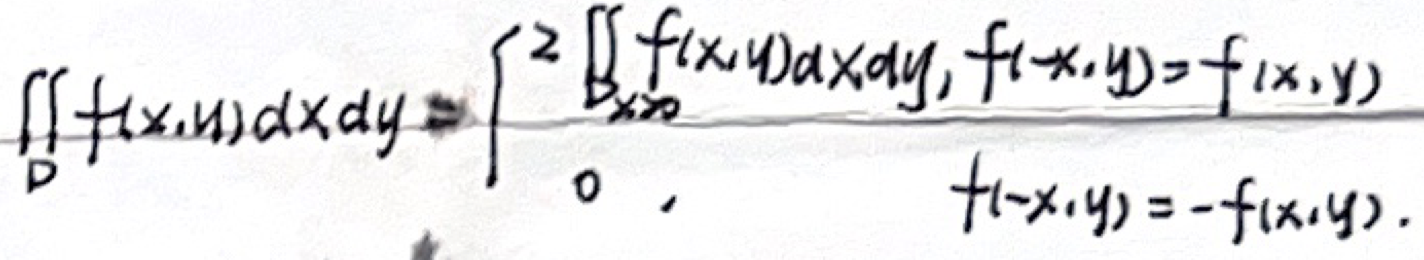
「奇偶性」积分域 D 关于 x 轴对称

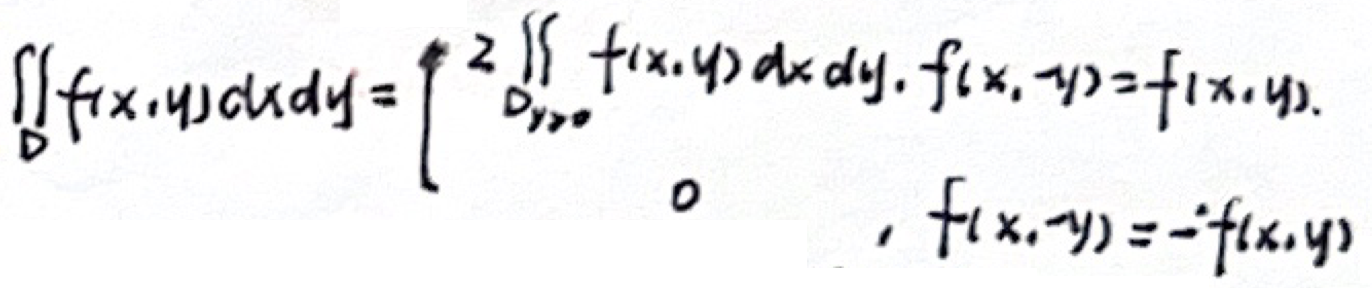
「轮换对称性」积分域 D 关于 y = x 对称（必用）

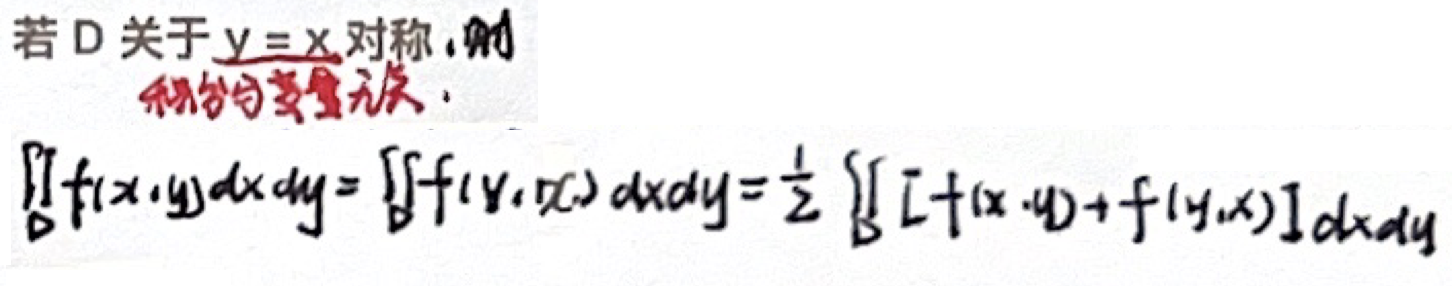
「形心公式」

$D$ 的形心坐标为 $(\overset{―}{x}, \overset{―}{y})$
- 形心坐标：几何中心（对称轴的交点）
则有

\iint_{D} x d x d y = \overset{―}{x} S_{D}, \iint_{D} y d x d y = \overset{―}{y} S_{D}

例题（二重积分）

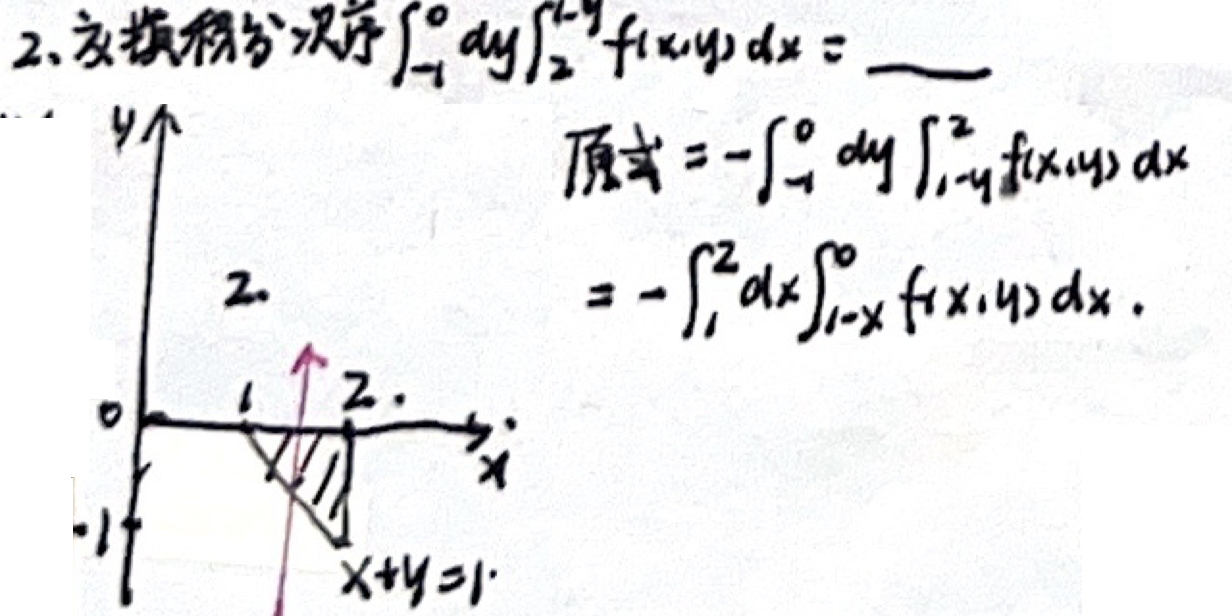
1. 直角坐标

例题一

例题二

例题三

例题四

例题五

例题六

例题七

2. 极坐标

偏心圆

例题一

例题二

「偏心圆总结」偏心圆的极坐标（两类重要偏心圆）

直角坐标 -> 极坐标

3.奇偶性

例题一

例题二

例题三

例题四

4.轮换对称性

例题一

例题二

例题三法一极坐标法二轮换对称性

例题四证明泊松积分

5.形心公式

例题一方法一方法二形心公式

二重积分求导