第十六节 多元函数极值与最值

「无约束极值」定义

「无约束极值」必要条件

「无约束极值」充分条件（AC-B^2判别法）

• $AC-B^2$ 判别法

「条件极值」及拉格朗日乘数法

• 步骤一
  • 求 $Z=f(x,y)$ 在约束条件 $\phi (x,y)=0$ 下的极值为边界最值
  • 令 $L(x,y,\lambda )=f(x,y)+\lambda \phi (x,y)$
  • 则 $L(x,y,\lambda )$ 分别为 $x,y,\lambda$ 求偏导数

$$L(x,y,\lambda )=\{\begin{array}{r}{f}_x^{\prime }+\lambda {\phi }_x^{\prime }(x,y)=0\\ f_y^{\prime }+\lambda {\phi }_y^{\prime }(x,y)=0\\ \phi (x,y)=0\end{array}$$

• 消 $\lambda$，得驻点即可能的极值点

• 步骤二

  • 比较各驻点的函数值，最大的为最大值，最小的为最小值。

「函数最值」多元函数最大值最小值

1. 求连续函数$f(x,y)$ 在有界闭区域 D 上的最大值最小值
   1. 求 $f(x,y)$ 在 D 内部可能的极值点
      • $\iff f(x,y)$在 D 内的驻点
   2. 求 $f(x,y)$ 在 D 的边界上的最大最小值
      • $\iff f(x,y)$ 在 D 的边界上的条件极值
   3. 比较各驻点处的函数值与条件极值
      • 最大的为最大值，最小的为最小值
2. 应用题
   1. $z=f(x,y)$
   2. 按照 #1 的三部曲求解

例题

「多元函数微分」判断多元函数(0,0)点连续

• 选（C)
• 大白话
  • 就是判断分子次幂是不是大于分子次幂，再判断一下分母代入1的时候等不等于0
  • 第二种判断方法就是把 $x$ 换成 $\rho cosx$， $y$ 换成 $\rho sinx$ ，这个时候 $\rho$ 趋向于0
• 具体判断
  • 当判断函数 $(0,0)$ 是否连续的时候，也就是极限$(x,y)\to (0,0)$
  • 若分子次方 m > 分母次方 n ，分别把 $x=1$，$y=1$ 代入分母中，
    • 若有分母等于0，则极限不存在，函数不连续
    • 若分母均不等于0，则函数连续
  • 分子次方 m < 分母次方 n ，函数不连续

「多元函数微分」链式求导法则

• z对x求偏导，变成
  • z对u求偏导，u对x求偏导
  • z对v求偏导，v对x求偏导
• 同理，z对y求偏导，变成
  • z对v求偏导，v对y求偏导

「多元函数微分」求重极限

「多元函数微分」证明重极限不存在

「多元函数微分」极坐标推广 + 换元

「多元函数微分」求偏导数值（先代后导）

• 一阶偏导数
  • 先代，后导，结果不变

例题一

• 

例题二

• 

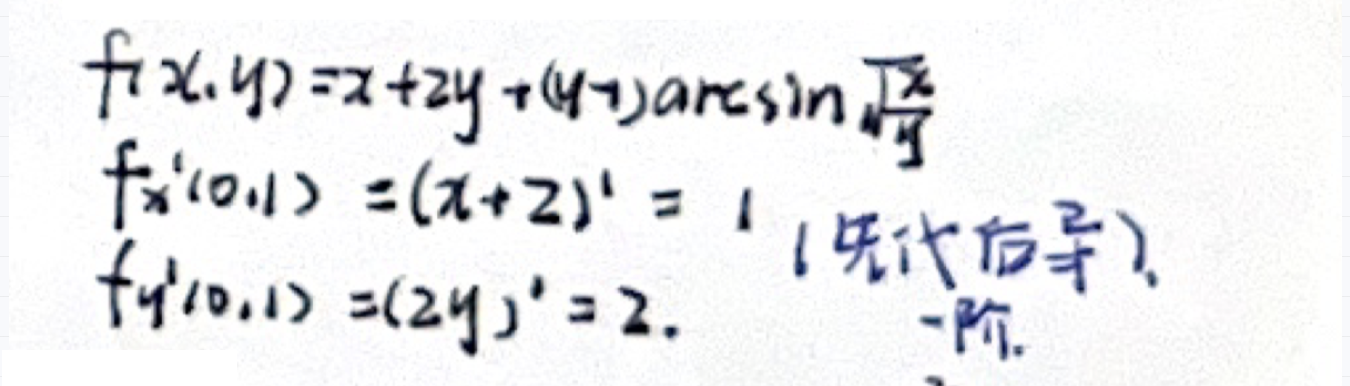
• 二阶偏导数

  • 先导，后代，再导

• 

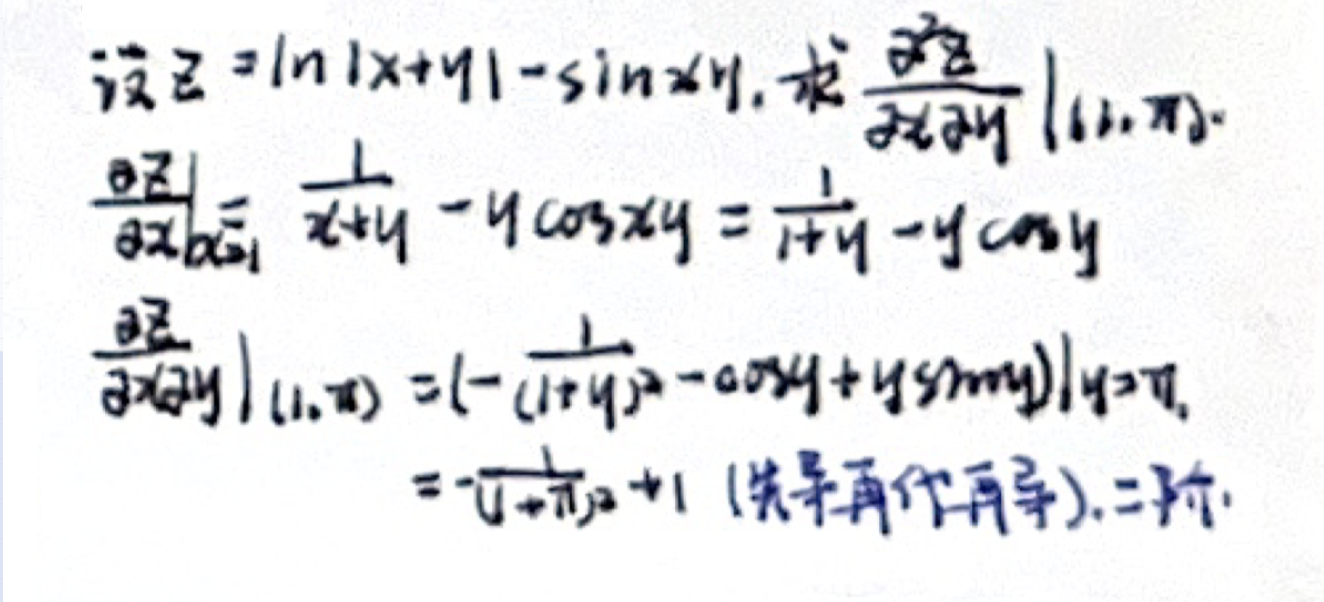
「多元函数微分」偏不定积分

「多元函数微分」全微分

「多元函数微分」全微分定义

「多元函数微分」高阶偏导

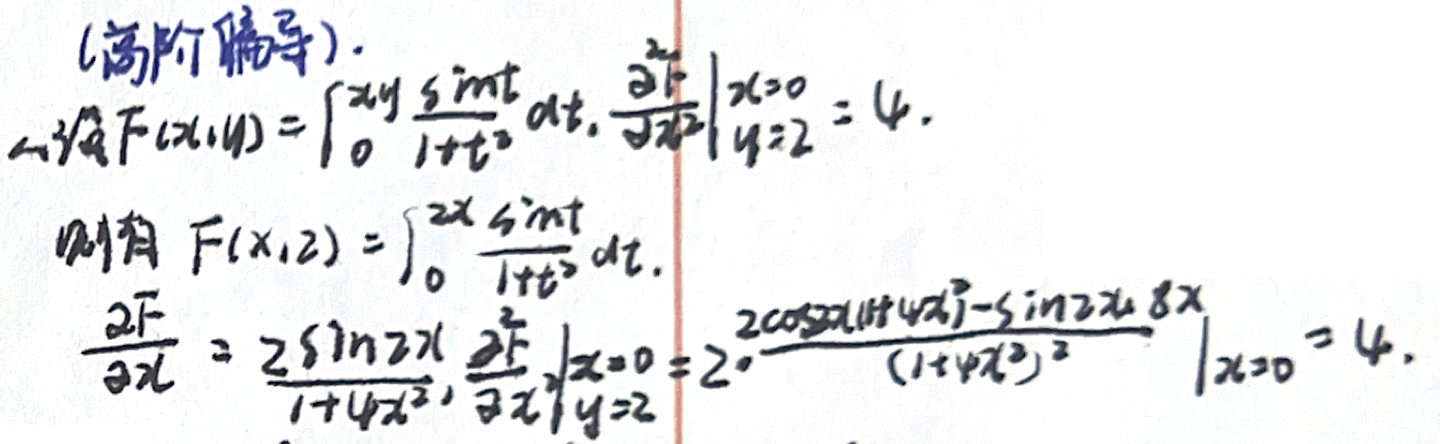
「多元函数极值最值」条件极值

「多元函数极值最值」最大值最小值

法一 拉格朗日乘数法

法二 转化为一元函数极值

法三 极坐标（用于解决圆和椭圆）

「多元函数极值最值」隐函数偏导、微分

例题一

例题二

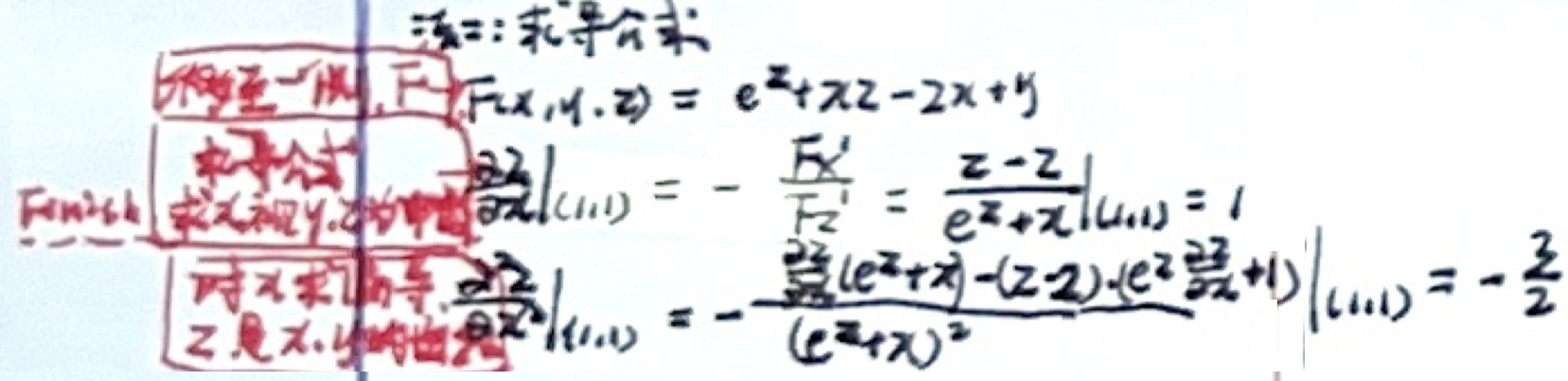
「多元函数极值最值」极值

ex1

ex2

ex3 椭圆点到直线距离最小值