第三节 函数的连续性

「连续性」定义

连续性
定义	函数在 $x_0$ 的邻域有定义，且左极限 = 右极限 = 该点处的函数值 ${\displaystyle \mathrm{连}\mathrm{续}\iff \underset{\mathrm{\Delta }x\to 0}{lim}\mathrm{\Delta }y=\underset{\mathrm{\Delta }x\to 0}{lim}[f(x_0+\mathrm{\Delta }x)-f(x_0)]=0\iff x_0\mathrm{邻}\mathrm{域}\mathrm{有}\mathrm{定}\mathrm{义}\underset{x\to x_0}{lim}f(x)=f(x_0)}$
定理	$f(x)$ 在点 $x_0$ 处连续的充要条件是 $f(x)$ 在点 $x_0$ 既左连续又右连续 ${\displaystyle \underset{x\to x_0^{-}}{lim}f(x)=f(x_0),\underset{x\to x_0^{+}}{lim}f(x)=f(x_0)}$

「间断点」定义 & 分类

• 间断点：在 $x_0$ 的去心邻域有定义，但在 $x_0$ 不连续

间断点分类	第一类间断点 --- 左右极限都存在	第二类间断点 --- 左右极限至少有一个不存在
	1. 可去间断点：左右极限都存在且相等 2. 跳跃间断点：左右极限都存在但不相等	3. 无穷间断点 ${\displaystyle \underset{x\to x_0^{+}}{lim}f(x)=\mathrm{\infty }}$， ${\displaystyle \underset{x\to x_0^{+}}{lim}f(x)=-\mathrm{\infty }}$ 4. 振荡间断点 ${\displaystyle y=\sin \frac{1}{x}}$

不在端点（无定义点）讨论间断点

• 在点 $x_0$ 的某去心邻域有定义，才讨论间断点。
• 如图所示情况，$f(x)$ 在点 $x=x_0$ 处只有右侧邻域有定义，故不讨论点 $x=x_0$ 是否为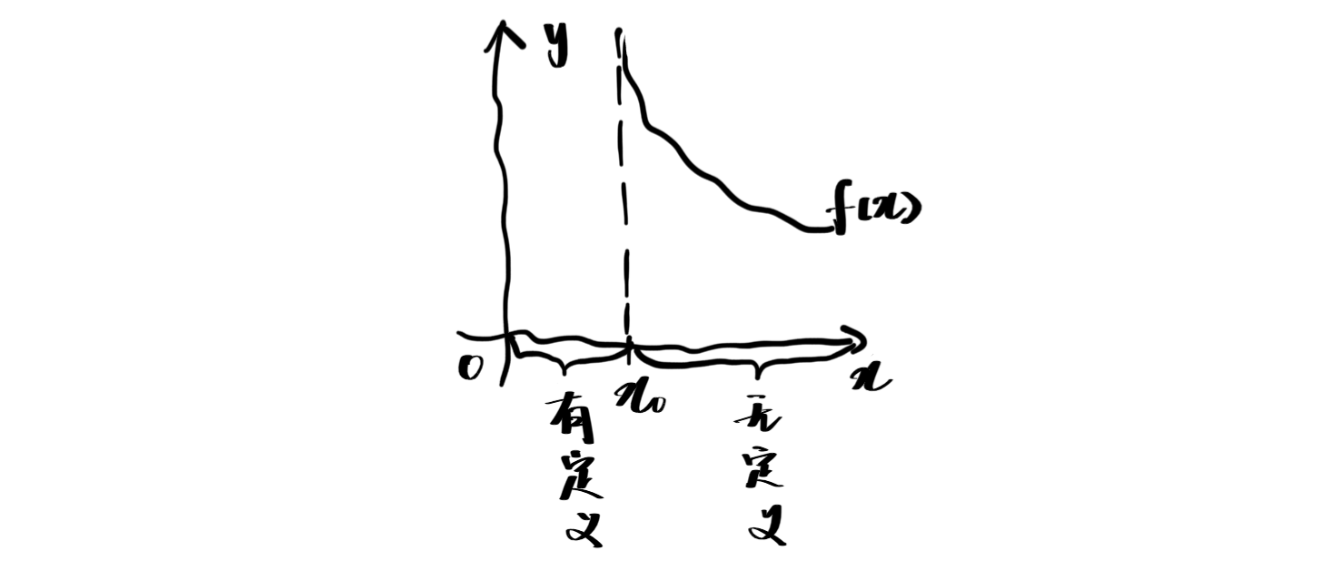间断点。

「连续性」运算与性质

• $f(x)$ 和 $g(x)$ 在 $x_0$ 处连续，则其和差商积均连续
• 复合函数连续
• 基本初等函数在定义域内连续
• 初等函数在定义区间内连续

「最值定理」定义

• $[a,b]$ 有 $f(x)$ 连续，$f(x)$ 在 $[a,b]$ 上必有最大值和最小值。

「有界性定理」定义

• $[a,b]$ 有 $f(x)$ 连续，$f(x)$ 在 $[a,b]$ 上必有界。

「介值定理」定义

• $[a,b]$ 有 $f(x)$ 连续，$f(a)\ne f(b)$，$c$ 介于 $f(a),f(b)$之间，$\mathrm{\exists }\xi \in (a,b)$ ，使得 $f(\xi )=c$。

「介值定理」推论

• $[a,b]$ 有 $f(x)$ 连续，可以取到介于最小值 m 和最大值 M 之间的任何值。

「零点定理」定义

• $[a,b]$ 有 $f(x)$ 连续，$f(a)·f(b)<0$，至少存在一点 $\xi \in (a,b)$ ，使得 $f(\xi )=0$。