第五章树与二叉树

第一节树

「树」定义

树：树是个结点的有限集；可以为空树。
结点的度：树中一个结点的孩子个数，称为结点的度。
树的度：树中结点的最大度数。
路径：两个结点之间所经过的结点序列。
路径长度：路径上所经过的边的个数。
森林：森林是一棵互不相交的树的集合。

「树」性质

「题」

【2010 统考真题】在一棵度为 4 的树 T 中, 若有 20 个度为 4 的结点, 10 个度为 3 的结点, 1 个度为 2 的结点, 10 个度为 1 的结点, 则树 T 的叶结点个数是( )。

第二节二叉树

「二叉树」定义

二叉树：是 $n (n \geq 0)$ 个结点的有限集合；可为空树。

二叉树和度为2的有序树的区别

度为2的有序树至少有3个结点，而二叉树可以为空
度为2的有序数左右次序是相对于另一个孩子而言，二叉树是确定的

「二叉树」存储

结构表示链式存储初始化

c++

struct TreeNode {
    ElemType value; //结点中的数据元素
    bool isEmpty; //结点是否为空
};

TreeNode t [MaxSize]; //按照完全二叉树的顺序存储

c++

typedef struct BiTNode{
    ELemType data; //数据域
    struct BiTNode *lchild, *rchild; //左、右孩子指针
}BiTNode ,*BiTree;

c++

//定义一棵空树
BiTree root = NULL;
//插入根节点
root = (BiTree) malloc(sizeof(BiTNode));
root-> data = {1};
root-> lchild = NULL;
root-> rchild = NULL;
//插入新结点
BiTNode * p = (BiTNode *) malloc(sizeof(BiTNode));
p->data = {2};
p-> lchild = NULL;
p-> rchild = NULL;
root->lchild = p; //作为根节点的左孩子

「二叉树」遍历

先序遍历中序遍历后序遍历层序遍历

c++

// 根 左 右
void PreOrder(BiTree T){
    if(T!=NULL){
        visit(T); //访问根结点
        PreOrder(T->lchild); //递归遍历左子树
        PreOrder(T- ->rchild); //递归遍历右子树
    }
}

c++

// 左 根 右
void PreOrder(BiTree T){
    if(T!=NULL){
        PreOrder(T->lchild); //递归遍历左子树
        visit(T); //访问根结点
        PreOrder(T- ->rchild); //递归遍历右子树
    }
}

c++

// 左 右 根
void PreOrder(BiTree T){
    if(T!=NULL){
        PreOrder(T->lchild); //递归遍历左子树
        PreOrder(T- ->rchild); //递归遍历右子树
        visit(T); //访问根结点
    }
}

c++

// 将根节点入队
// 队列非空
	// 将队头出队，访问该节点
    // 将该节点的左、右孩子依次插入队尾
// 重复直至队列为空

//链式队列结点
typedef struct LinkNode{
    BiTNode * data; //保存的是节点的指针
    struct LinkNode *next;
}LinkNode;

typedef struct{
    LinkNode *front, *rear; //队头队尾
}LinkQueue;

//层序遍历
void Level0rder(BiTree T){
    LinkQueue Q;
    InitQueue(Q); 					//初始化辅助队列
    BiTree p;
    EnQueue(Q,T); 					//将根结点入队
    while(!IsEmpty(Q)){ 			//队列不空则循环
        DeQueue(Q，p); 			   //队头结点出队
        visit(p); 					//访问出队结点
        if(p->lchild != NULL)
        	EnQueue(Q, p->lchild);  //左孩子入队
        if(p->rchild != NULL)
        	EnQueue(Q, p->rchild);  //右孩子入队
    }
}

「二叉树」性质

「二叉树」顺序存储结构

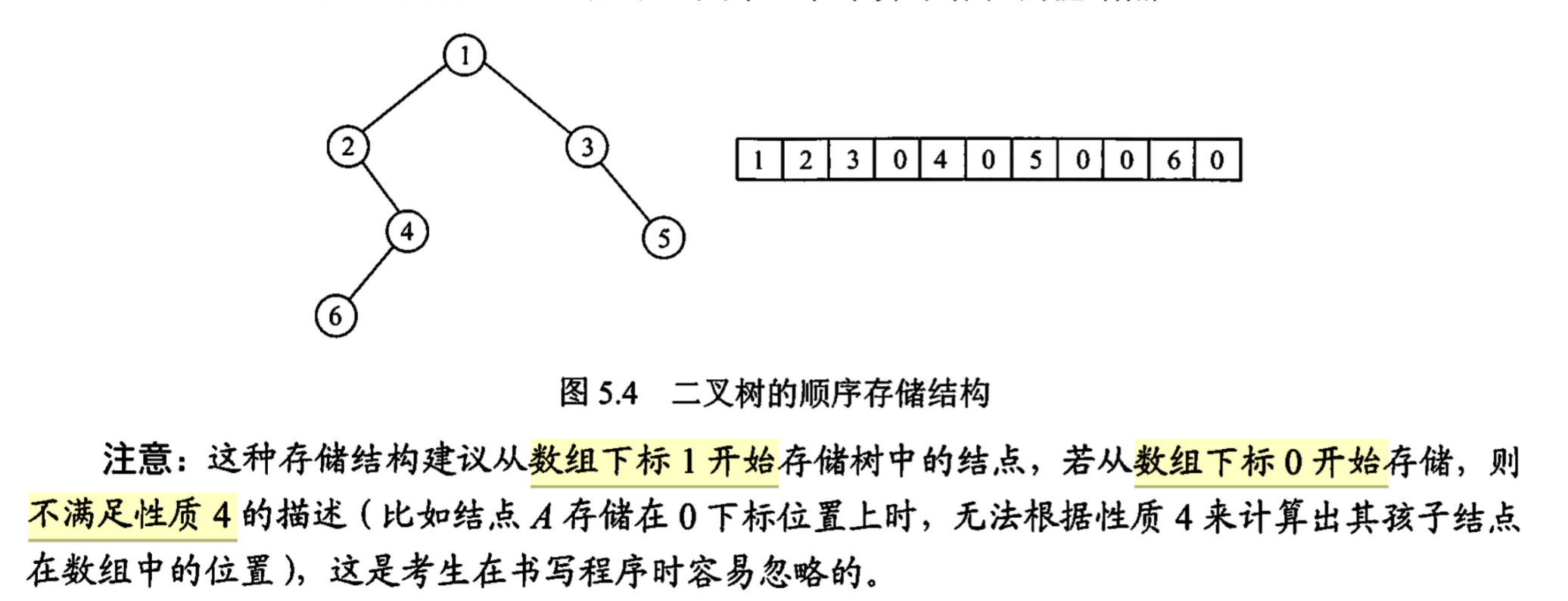
「二叉树」链式存储结构

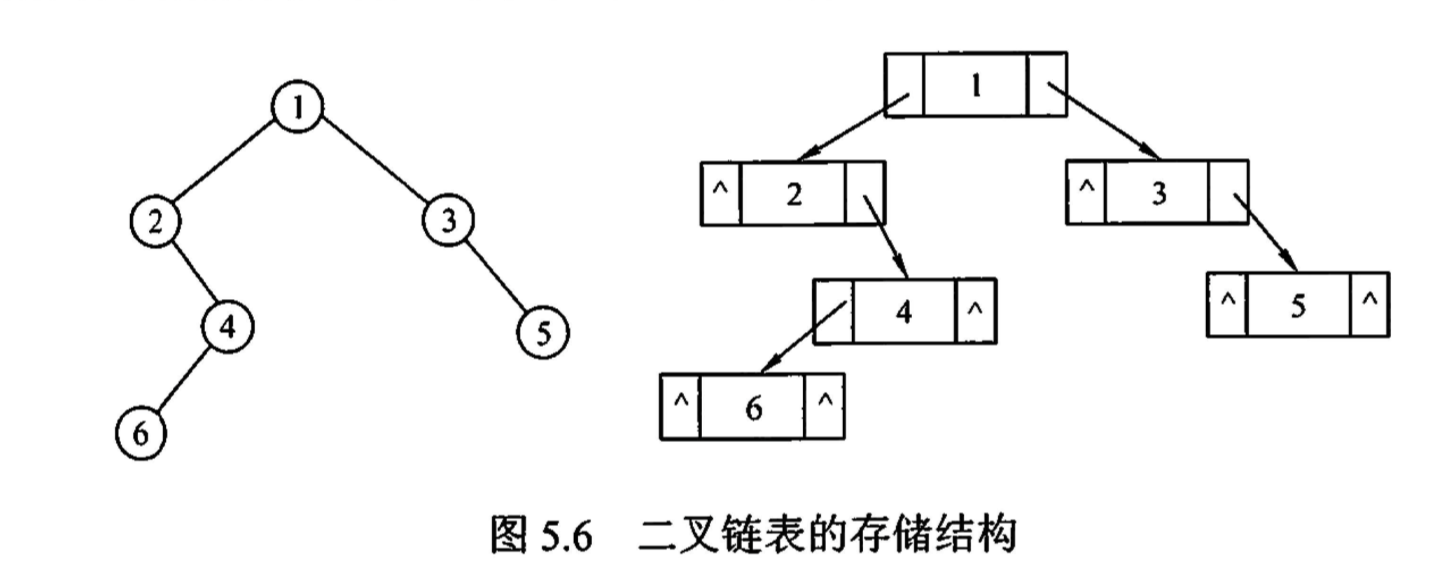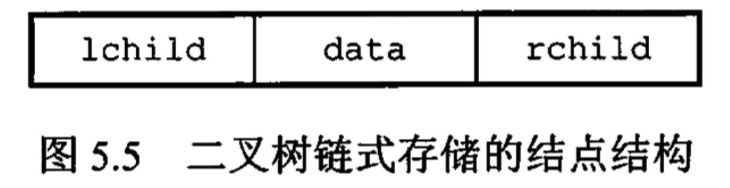cpp

class BitNode{
	ElemType data; //数据域
	BitNode *lchild. *rchild; //左、右孩子指针
}

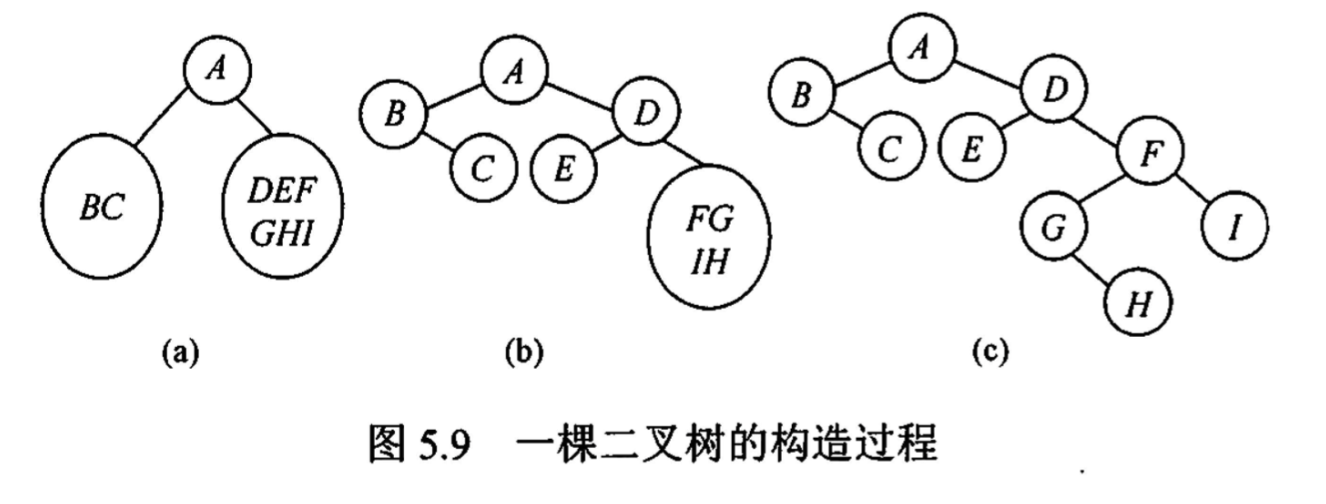
「二叉树」遍历序列构造二叉树

唯一的确定一颗二叉树
- 先序+中序
  - 先序中，第一个结点为二叉树根节点，该结点在中序中，把中序序列分割成两个子序列；左子序列第一个结点为左子树根节点，如此递归循环
- 后序+中序
  - 同理，后序中，最后一个结点为二叉树根节点，如同先序般划分
- 层序+中序
  - 层序中，第一个结点为二叉树根节点，第二个结点为二叉树左子树的根节点，以此类推。
注：先序+后序 无法唯一的确定一颗二叉树。

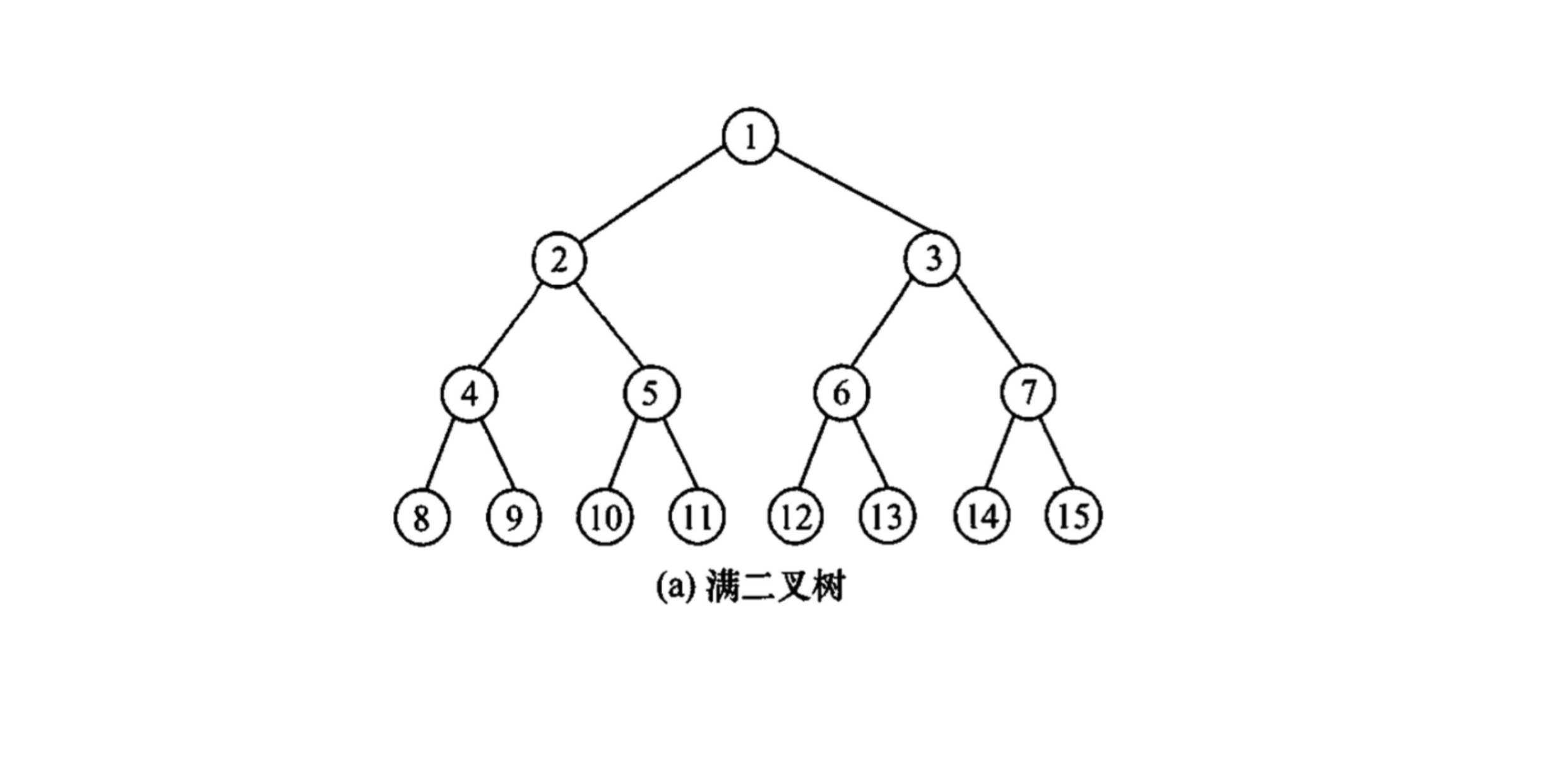
「满二叉树」定义

高度为 $h$ ，含有 $2^{h} - 1$ 个结点的二叉树
树中的每层都含有最多的结点
叶节点集中在二叉树的最后一层
除叶结点的每个结点度数均为2

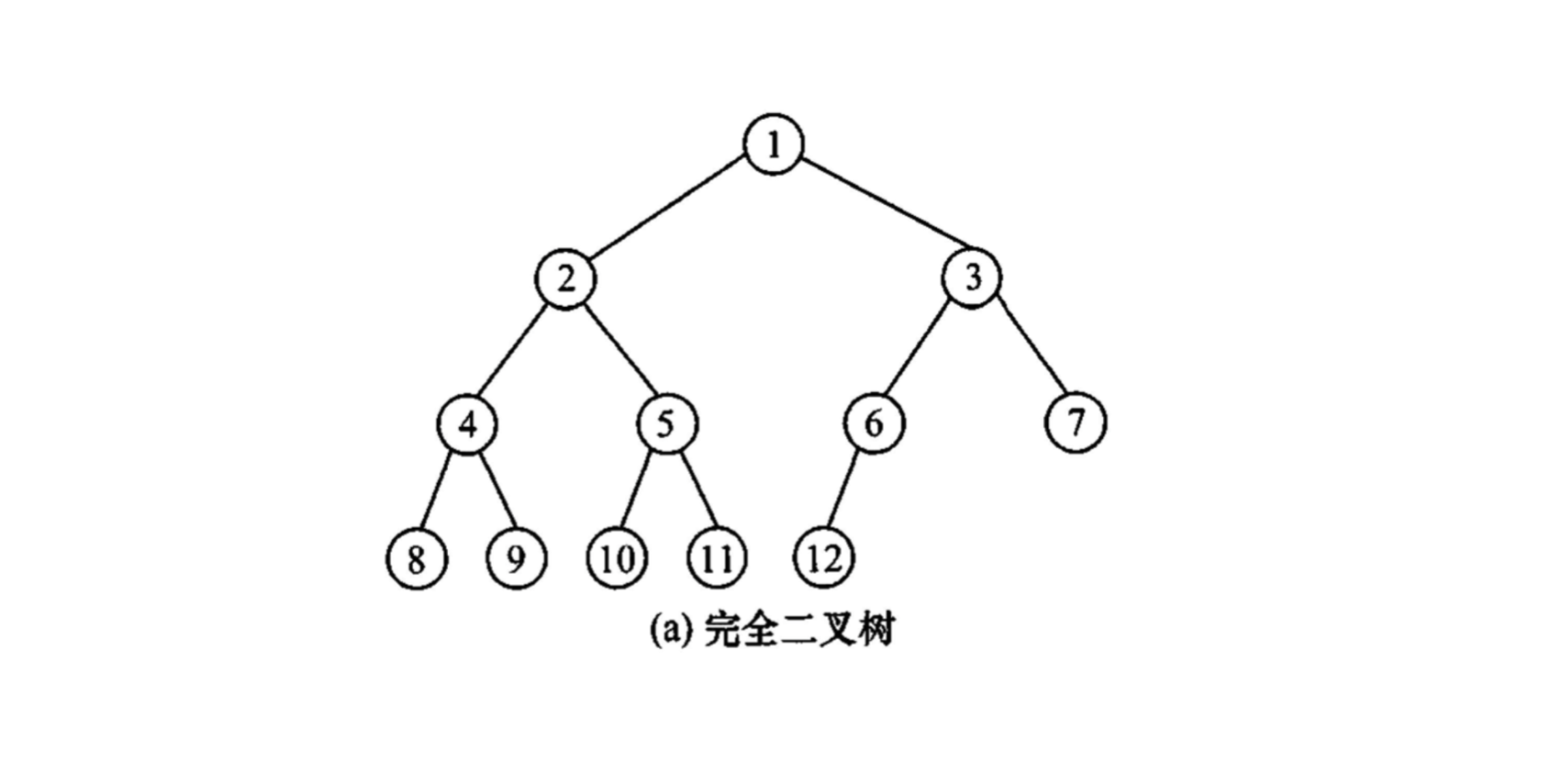
「完全二叉树」定义

高度为h，有n个节点的二叉树

完全二叉树的特点

「二叉排序树」定义

左子树上所有结点关键字均小于根节点关键字
右子树上所有结点关键字均大于根节点关键字

「二叉排序树」删除

树上任意一个结点的左子树和右子树的深度之差不超过1

叶子：直接删
只有左/右子树：直接删，用子树顶替
同时有左右子树
- 用后继节点顶替：右子树中最左下的
- 用前驱节点顶替：左子树中最右下的

「平衡二叉树」定义

树上任意一个结点的左子树和右子树的深度之差不超过1

「线索二叉树」定义（选择题）

规定
- 若无左子树，令lchild指向其前驱结点
- 若无右子树，令rchild指向去后继结点
- 增加两个标志域标识指针域以指向左（右）孩子或前驱（后继）

标志域的含义

ltag = 0，lchild域指示结点的左孩子
ltag = 1，lchild域指示结点的前驱
rtag = 0，lchild域指示结点的右孩子
rtag = 0，lchild域指示结点的后继

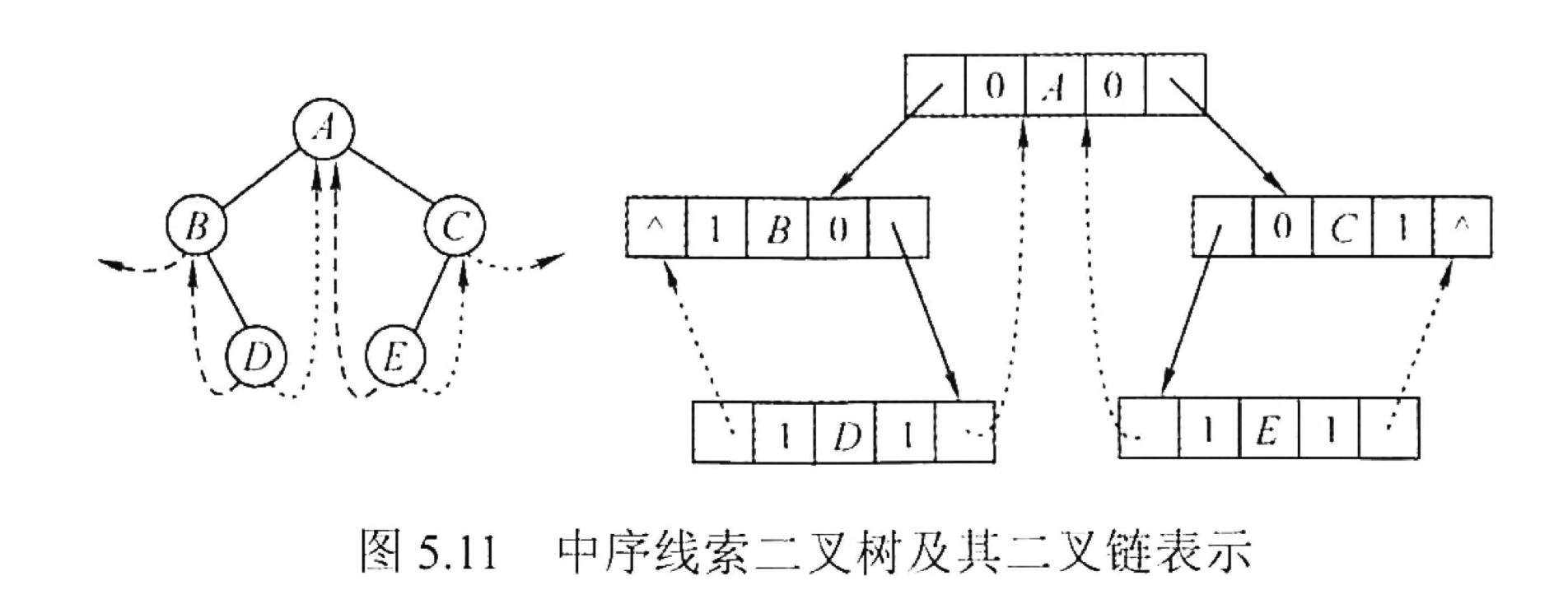
「线索二叉树」中序线索二叉树

线索二叉树的存储结构描述中序线索化

c++

//全局变量pre,指向当前访问结点的中(前、后)序前驱
ThreadNode *pre=NULL;

typedef struct BiTNode{
    ELemType data; //数据域
    struct BiTNode *lchild, *rchild; //左、右孩子指针
    int ltag, rtag; //左、 右线索标志：0表示孩子，1表示线索
}BiTNode ,*BiTree;

c++

void visit(ThreadNode *q) {
    if(q->lchild == NULL) { //当前节点左子树为空,建立前驱线索
        q->lchild = pre;
        q->ltag = 1;
    }
    if(pre != NULL && pre->rchild == NULL) {
        pre->rchild = q; //前驱结点的右子树为空，建立后继线索
        pre->rtag = 1;
    }
    pre=q;
}

前序与后序

前后序类似，注意
- 最后再修改一次pre的后继节点为null
- 遍历时判断左右子树是孩子还是线索

孩子-兄弟表示法

树	森林	二叉树
先根遍历	先序遍历	先序遍历
后根遍历	中序遍历	中序遍历

「线索二叉树」中序线索二叉树的构造

TIP

线索化的实质就是遍历一遍二叉树。
线索化二叉树其实就是把树先排序，就直接找到前驱后继。

pre 指向访问过的节点，p 指向当前访问的结点，即 pre 指向 p 的前驱。
在中序遍历的过程中，检查 p 的左指针是否为空，若为空就将它指向 pre；
检查 pre 的右指针是否为空，若为空就将它指向 p。

「AVL树」结点数量

$h$ 为树高
$n_{h}$ 为树高为 $h$ 时的最小节点数

\begin{matrix} n_{0} = 0 \\ n_{1} = 1 \\ n_{2} = 2 \\ n_{h} = 1 + n_{h - 1} + n_{h - 2} \end{matrix}

「AVL树」插入

（在某节点的）L【左孩子】（的）R【右子树】（中插入导致不平衡）

LL：左孩子右上旋
RR：右孩子左上旋
LR
- 左孩子的右孩子左上旋，变成新的左孩子
- 新的左孩子右上旋
RL
- 右孩子的左孩子右上旋，变成新的右孩子
- 新的右孩子左上旋

「哈夫曼树」定义

权值最小的两个组成兄弟
根节点的权值等于两个孩子相加
由n个节点建立哈夫曼树的过程中新建了n-1个节点

「红黑树」定义

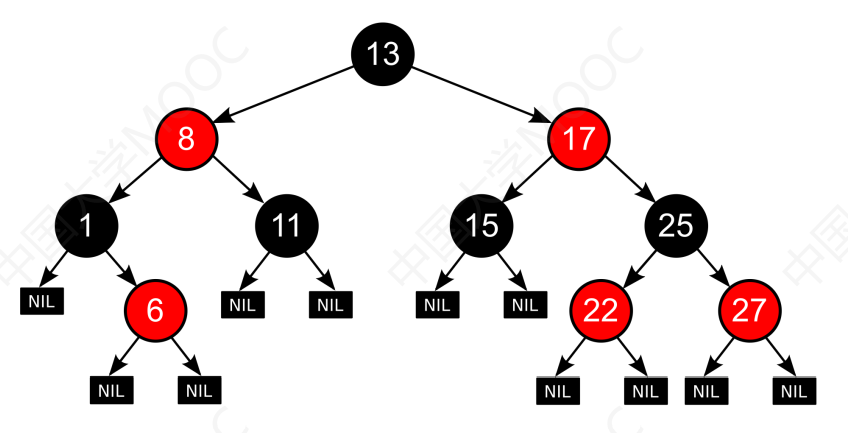
本质是二叉排序树：左<根<右
结点只有两种颜色
根结点是黑色的
叶结点（失败结点、NULL结点）是黑色的
没有两个相邻的红节点
从任何一个结点到叶子节点的简单路径上黑节点的数量相同
设共有n个节点，则红黑树的树高： $h \leq 2 l o g 2 (n + 1)$

红黑树的数据结构描述

c++

struct RBnode{
    int key;
    RBnode* parent;		//父节点
    RBnode* lChild;		//左孩子
    RBnode* rChild;		//右孩子
    int color;			//结点颜色
}

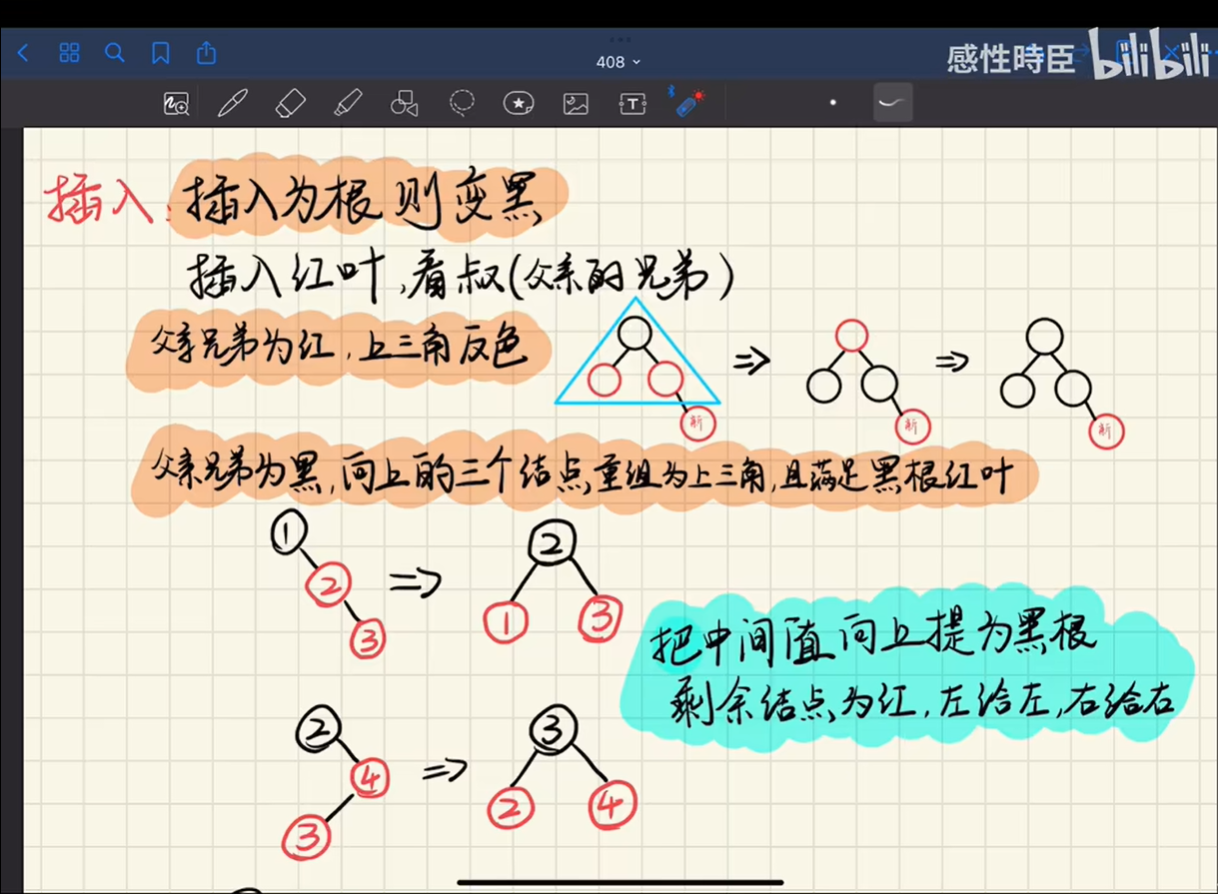
「红黑树」插入原则

确定插入位置（同二叉排序树）
- 新节点是根：染为黑色
- 新节点非根：染为红色
若插入后满足特性，插入结束
- 插入只会破坏 “没有两个相邻的红节点” 这一特性
- 除非是根节点，只要满足这一特性即可
否则，观察叔叔节点（父节点的兄弟）
- 叔叔节点为黑色：旋转+染色
  - LL：右旋，父换爷+染色
  - RR：左旋，父换爷+染色
  - LR：左、右旋，儿换爷+染色
  - RL：右、左旋，儿换爷+染色
- 叔叔节点为红色
  - 叔、父、爷染色，将爷节点视为新节点再继续处理

「并查集」表示

通过森林表示多个集合
使用双亲表示法来存储并查集
- 每个节点中保存指向双亲的“指针”
- 根节点指针为-1
查：向上遍历，找到根节点，判断是否在同一个集合里
并：将两棵树的根节点相连

并查集的数据结构描述初始化查操作并操作

c++

#define SIZE 13;
int UFSets[SIZE];		//数组中存储每个节点的根

c++

void Initial(int S[]){
    for(int i=0; i<SIZE; i++){
        S[i]=-1;		//先全部设为单独的子集
    }
}

c++

int Find(int S[], int x){
    while(S[x]>=0){
        x = S[x];
    }
    return x;
}

c++

void Union(S[], int Root1, int Root2){
    if(Root1 != Root2){
        S[Root2] = Root1;
    }
}

并查集的时间复杂度

并： $O (1)$
查： $O (n)$

「并查集」对union操作的优化

让高度低的树成为子树
根节点的绝对值表示树中的节点总数（-6、-3……）
合并时将根节点相加
树高不超过 $⌊ l o g_{2} n ⌋$

c++

void Union(S[], int root1, int root2){
    if(root1 != root2){
        if(S[root2] > S[root1]){
            S[root1] += S[root2];	//累加节点总数
            S[root2] = S[root1];	//小树合并到大树
        }else{
            S[root2] += S[root1];
            S[root1] = S[root2];
        }
    }
}

「并查集」对find操作的优化

在查找某个节点找到根节点后，将路径上所有的节点都直接挂到根节点下

c++

int Find(int S[], int x){
    int root = x;
    while(S[x]>=0){
        root = S[x];
    }
    while(x != root){
        int temp = S[x];
        S[x] = root;
        x = remp;
    }
    return root;
}

A111.高等数学

A112.线性代数

A113.概率论与数理统计

A212.C++

A214.Swift

A221.数据结构

A222.计算机组成原理

A223.计算机操作系统

A224.计算机网络

1231.常见算法

第五章树与二叉树

第一节树

「树」定义

「树」性质

「题」

第二节二叉树

「二叉树」定义

「二叉树」存储

「二叉树」遍历

「二叉树」性质

「二叉树」顺序存储结构

「二叉树」链式存储结构

「二叉树」遍历序列构造二叉树

「满二叉树」定义

「完全二叉树」定义

「二叉排序树」定义

「二叉排序树」删除

「平衡二叉树」定义

「线索二叉树」定义（选择题）

「线索二叉树」中序线索二叉树

「线索二叉树」中序线索二叉树的构造

「AVL树」结点数量

「AVL树」插入

「哈夫曼树」定义

「红黑树」定义

「红黑树」插入原则

「并查集」表示

「并查集」对union操作的优化

「并查集」对find操作的优化

第五章 树与二叉树 ​

第一节 树 ​

「树」定义 ​

「树」性质 ​

「题」 ​

第二节 二叉树 ​

「二叉树」定义 ​

「二叉树」存储 ​

「二叉树」遍历 ​

「二叉树」性质 ​

「二叉树」顺序存储结构 ​

「二叉树」链式存储结构 ​

「二叉树」遍历序列构造二叉树 ​

「满二叉树」定义 ​

「完全二叉树」定义 ​

「二叉排序树」定义 ​

「二叉排序树」删除 ​

「平衡二叉树」定义 ​

「线索二叉树」定义（选择题） ​

「线索二叉树」中序线索二叉树 ​

「线索二叉树」中序线索二叉树的构造 ​

「AVL树」结点数量 ​

「AVL树」插入 ​

「哈夫曼树」定义 ​

「红黑树」定义 ​

「红黑树」插入原则 ​

「并查集」表示 ​

「并查集」对union操作的优化 ​

「并查集」对find操作的优化 ​

第五章树与二叉树

第一节树

「树」定义

「树」性质

「题」

第二节二叉树

「二叉树」定义

「二叉树」存储

「二叉树」遍历

「二叉树」性质

「二叉树」顺序存储结构

「二叉树」链式存储结构

「二叉树」遍历序列构造二叉树

「满二叉树」定义

「完全二叉树」定义

「二叉排序树」定义

「二叉排序树」删除

「平衡二叉树」定义

「线索二叉树」定义（选择题）

「线索二叉树」中序线索二叉树

「线索二叉树」中序线索二叉树的构造

「AVL树」结点数量

「AVL树」插入

「哈夫曼树」定义

「红黑树」定义

「红黑树」插入原则

「并查集」表示

「并查集」对union操作的优化

「并查集」对find操作的优化