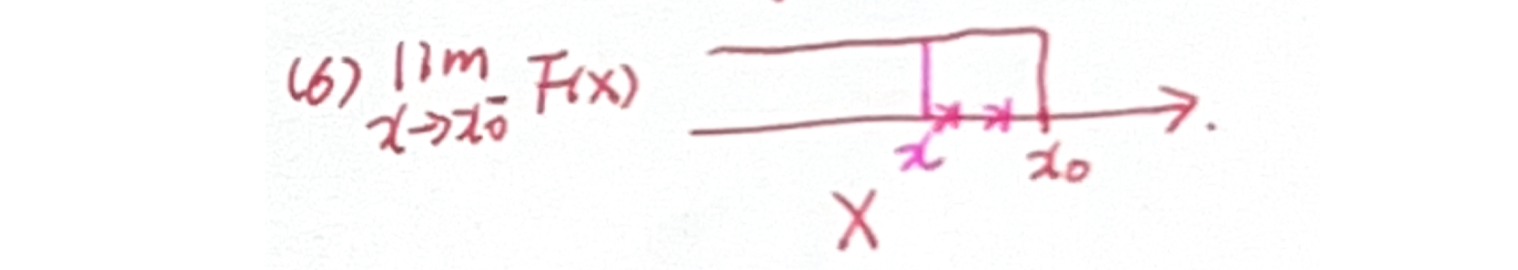第二章 一维随机变量及其分布

第一节 分布函数

「随机变量」定义

• 设试验的样本空间为 $\mathrm{\Omega }$，称实值函数 $X=X(\omega ),\omega \in \mathrm{\Omega }$ 为随机变量，简记作 $X$

「分布函数」定义

• 设 $X$ 为随机变量，对任意实数 $x$，称 $F(x)=P\{X\le x\}$ 为 $X$ 的分布函数

「分布函数」性质

共同构成充要条件	求 $F(X)$ 取值概率
1. 非负性 $0\le F(X)\le 1,-\mathrm{\infty }<x<+\mathrm{\infty }$	5. $P(a<X\le b)=F(b)-F(a)$
2. 规范性 $F(-\mathrm{\infty })=0,F(+\mathrm{\infty })=1$	6. $P(X=x_0)=F(x_0)-F(x_0-0)$
3. 单调不减 当$x_1<x_2$时，$F(x_1)\le F(x_2)$
4. 右连续 $F(x_0+0)=F(x_0)$

性质证明

2. 规范性 $F(-\mathrm{\infty })=0,F(+\mathrm{\infty })=1$
   1. $F(-\mathrm{\infty })=0\Rightarrow P\{X(\omega )\le -\mathrm{\infty }\}=P(\varphi )=0$
   2. $F(+\mathrm{\infty })=1\Rightarrow P\{X(\omega )\le +\mathrm{\infty }\}=P(\mathrm{\Omega })=0$
3. 右连续
   1. 
4. $P(a<X\le b)=F(b)-F(a)$
   1. $Pr:P\{X\le b\}-P\{X\le a\}=F(b)-F(a)$
5. $P(X=x_0)=F(x_0)-F(x_0-0)$
   1. 

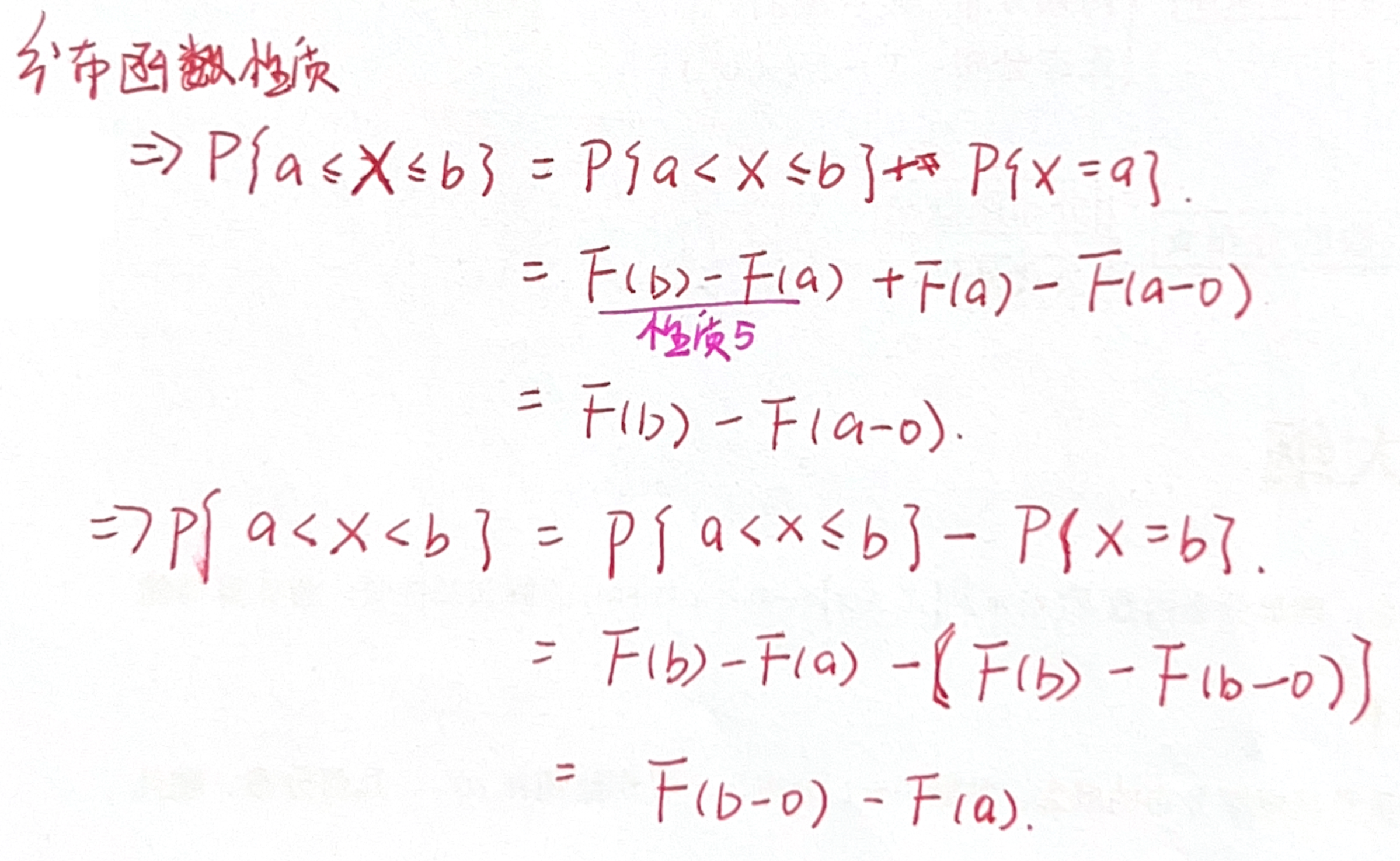
第二节 一维离散型随机变量

「概率分布」定义

「概率分布」性质

「评注」

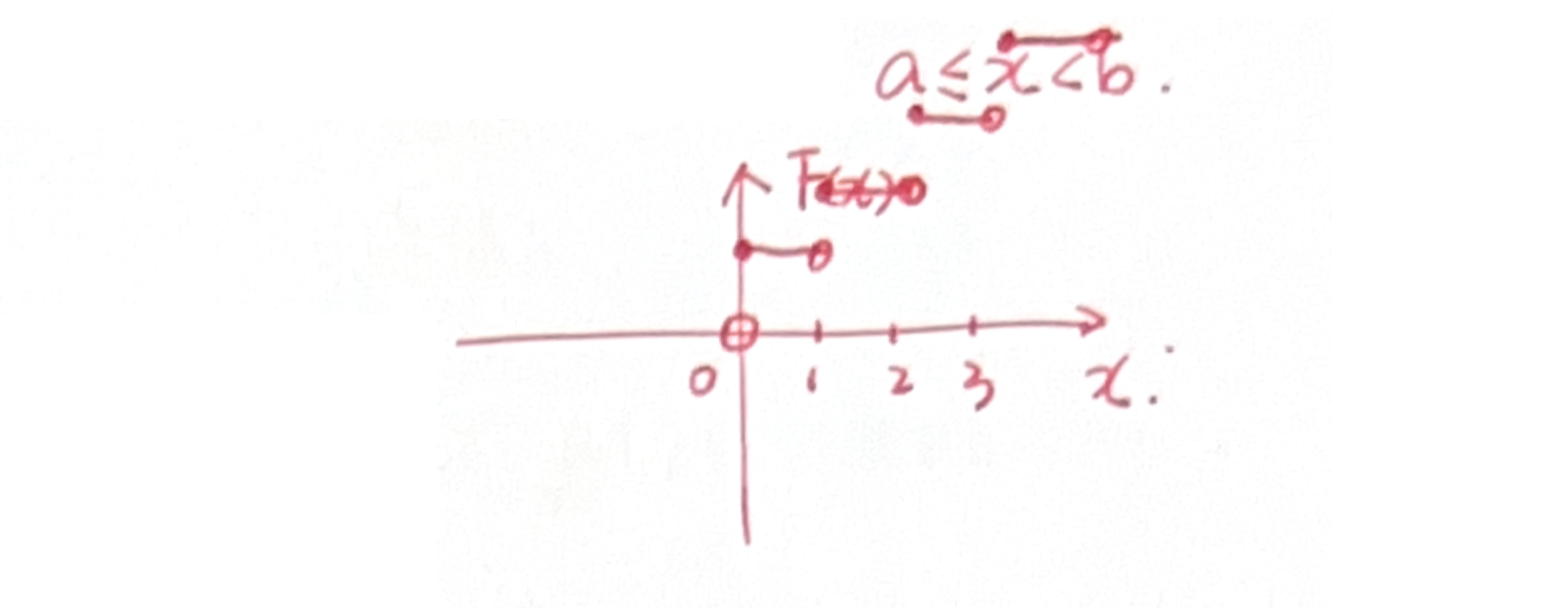
1. 当分布函数不连续时，为保证其右连续性，自变量 $x$ 的分段区间为左闭右开
2. 离散型随机变量的分布函数为右连续的阶梯函数

第三节 一维连续型随机变量

「概率密度」定义

• 设随机变量 $X$ 的分布函数为 $F(x)$，若存在非负可积函数 $f(x)$，对任意实数 $x$，有 ${\displaystyle F(x)={\int }_{-\mathrm{\infty }}^{x}f(t)dt}$，则称 $X$ 为连续型随机变量，$f(x)$ 为 $X$ 的概率密度或密度函数。

连续型随机变量取单点值的概率为0

「概率密度」性质

• 构成概率密度充要条件
  • （非负性）$f(x)>0,-\mathrm{\infty }<x<+\mathrm{\infty }$
  • （规范性）${\displaystyle {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(x)dx=1}$
• ${\displaystyle P\{a<X\le b\}={\int }_a^{b}f(x)dx}$

证明与评注

• 性质 (1)，(2) 构成概率密度的充要条件，用于判定概率密度或已知概率密度反求参数。
• 性质 (2) 证明： $Pr:F(+\mathrm{\infty })=1$
• 性质 (3) 用于计算随机变量取值的概率，可以推广为

$${\displaystyle P\{a<X\le b\}=P\{a\le X<b\}=P\{a\le X\le b\}=P\{a<X<b\}={\int }_a^{b}f(x)dx}$$

• 性质 (3) 证明：$Pr:{\displaystyle F(b)-F(a)={\int }_{-\mathrm{\infty }}^{b}f(x)dx-{\int }_{-\mathrm{\infty }}^{a}f(x)dx={\int }_a^{b}f(x)dx}$

第四节 八大分布

「八大分布」0-1 分布

「八大分布」二项分布

• 设 $X\sim B(1,p)$，则 $Y=n-X\sim B(n,1-p)$

「八大分布」泊松分布（Poisson）

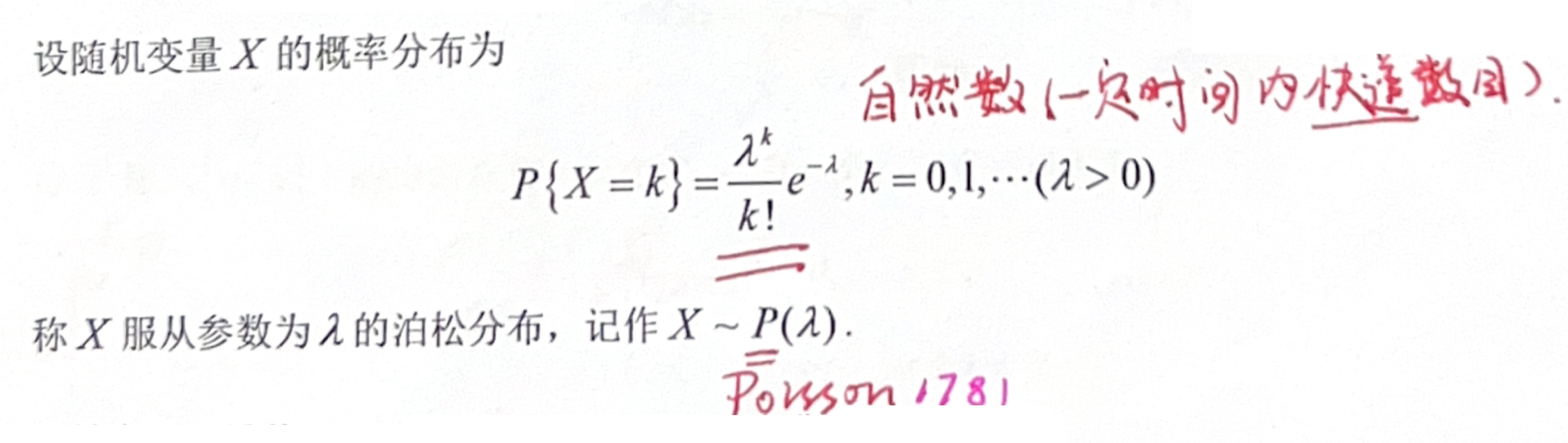
泊松定理

「八大分布」几何分布（Geometry）

「八大分布」超几何分布（Hyper）

「八大分布」均匀分布（Uniform）

「八大分布」指数分布（Exponent）

$\mathrm{\Gamma }$ 积分

「八大分布」正态分布（Normal）

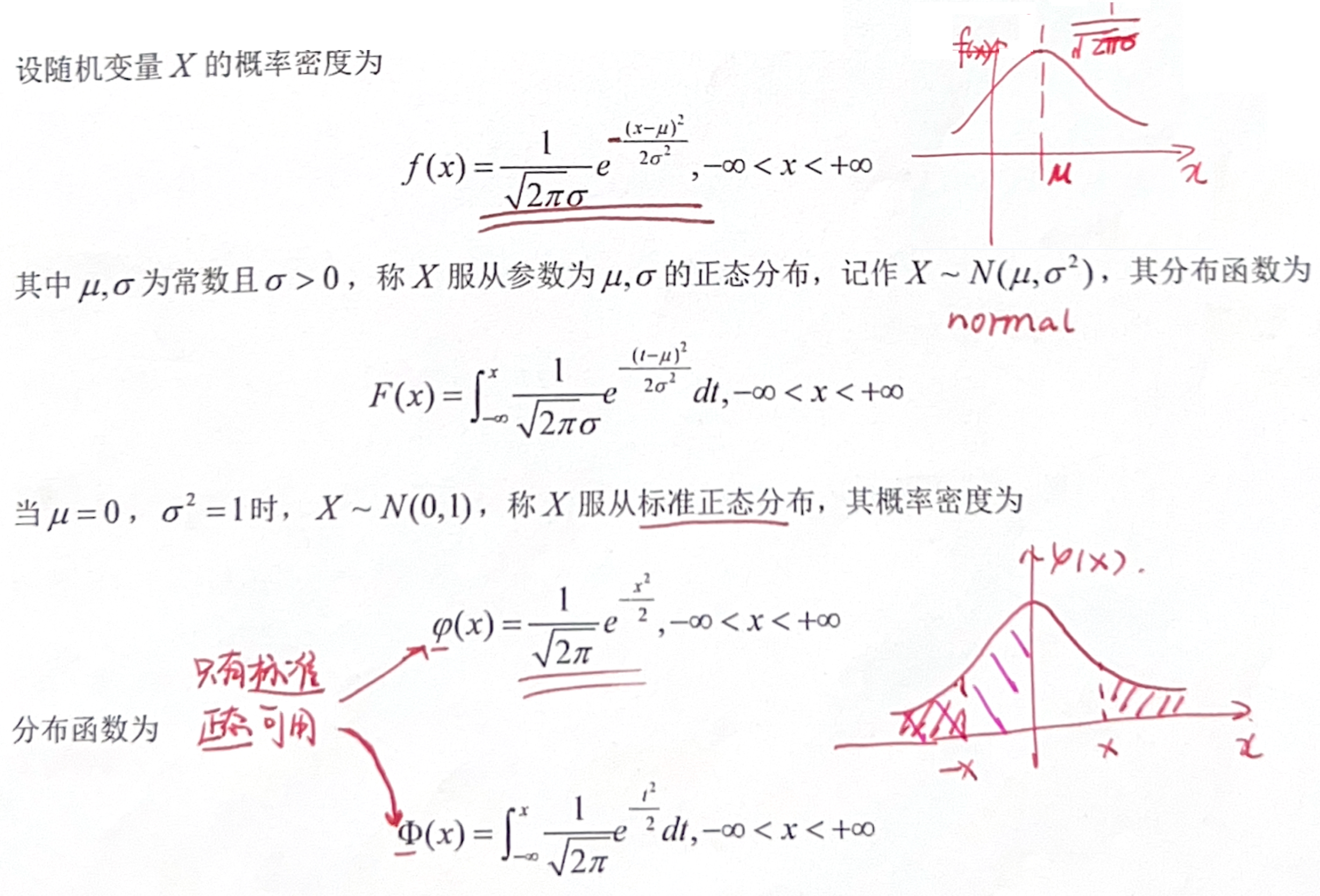
正态分布的性质

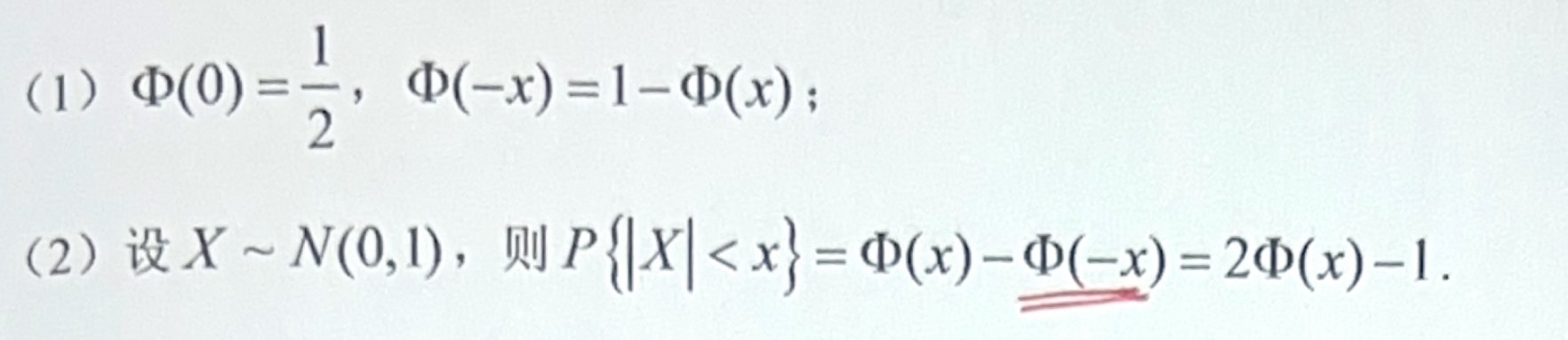
正态分布的标准化

推广

• $f(x)=A{e}^{-a{x}^2+bx+c}(a>0)$ 均为正态。

第五节 一维随机变量函数的分布

「一维分布」离散型随机变量的分布

「一维分布」连续性随机变量函数的分布

分布函数法

公式法（不可作水平线）