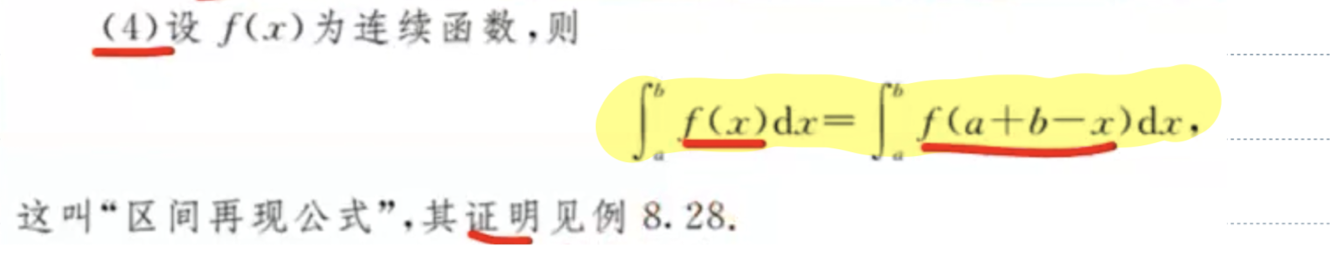第十节 定积分

「定积分」概念

• 分割、近似、求和、取极限

「定积分」定义

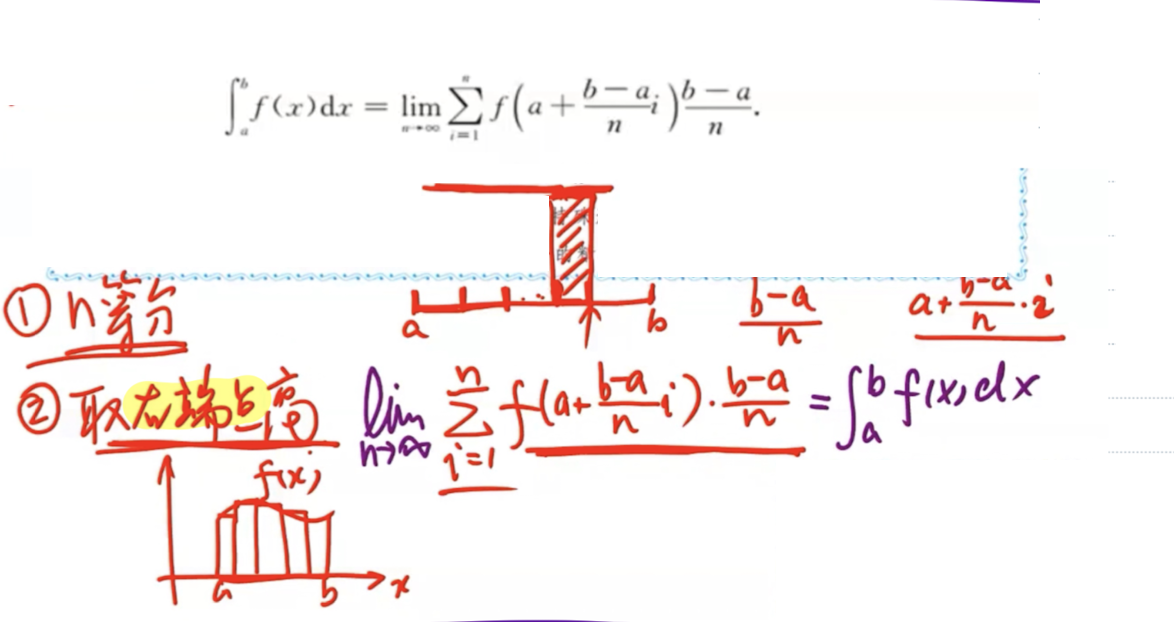
凑定积分定义

「定积分」性质

「定积分」积分的保号性

「定积分」积分估值定理

「定积分」存在的充分条件

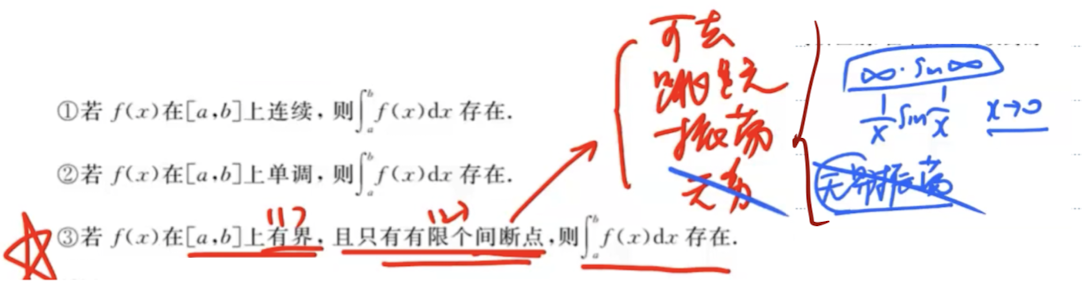
「定积分」存在的必要条件

有原函数用不定积分存在定理，有定积分用定积分存在定理

「定积分」几何意义

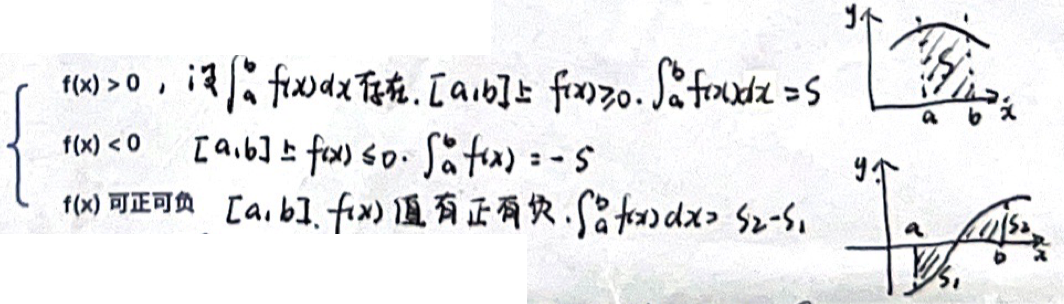
「定积分」不等式性质

• 若$f(x)\le g(x)$，则 ${\displaystyle {\int }_a^{b}f(x)dx\le {\int }_a^{b}g(x)dx}$
• 若 $M$ 和 $m$ 分别是 $f(x)$ 在 $[a,b]$ 上的最大值和最小值，则

$$m(b-a)\le {\int }_a^{b}f(x)dx\le M(b-a)$$

• 绝对值的积分大于积分的绝对值

$$|{\int }_a^{b}f(x)dx|\le {\int }_a^b|f(x)|dx$$

「定积分」积分中值定理

• $f(x)$ 在 $[a,b]$ 连续，则 ${\displaystyle {\int }_a^{b}f(x)dx=f(\xi )(b-a)(a<\xi <b)}$ ，称 ${\displaystyle \frac{1}{b-a}{\int }_a^{b}f(x)dx}$ 为 $y=f(x)$ 在 $[a,b]$ 上的平均值
  • 常用于证明题
• $f(x),g(x)$ 在 $[a,b]$ 连续，$g(x)$ 不变号，则 ${\displaystyle {\int }_a^{b}f(x)g(x)dx=f(\xi ){\int }_a^{b}g(x)dx(a\le \xi \le b)}$
  • 常用于变上限积分

「积分上限函数」定义

• ${\displaystyle {\int }_a^{x}f(x)dt}$ 是上限 $x$ 的函数，称为积分上限函数。
• $f(x)$ 在(a,b)上连续，则${\displaystyle \mathrm{\Phi }(x)={\int }_a^{x}f(t)dt}$ 在 $[a,b]$ 上可导，有 ${\displaystyle \frac{d\mathrm{\Phi }(x)}{dx}=f(x)}$
• 由原函数概念，$f(x)$ 在 $[a,b]$ 连续，$\mathrm{\Phi }(x)$ 为 $f(x)$ 的其中一个原函数
  • 知连续函数必有积分上限函数

「积分上限函数」求导数

• $f(x)$ 在 $[a,b]$ 上连续，${\phi }_1(x)、{\phi }_2(x)$ 可导，则

$$({\int }_{{\phi }_1(x)}^{{\phi }_2(x)}f(t)dt{)}^{\prime }=f[{\phi }_2(x)]\cdot {\phi }_2^{\prime }(x)-f[{\phi }_1(x)\cdot {\phi }_1^{\prime }(x)]$$

「积分上限函数」奇偶性

「定积分」计算（六大积分法）

「技」计算定积分时，有用的结论

「定积分」牛顿-莱布尼兹公式

「定积分」换元积分法（三换）

• 换被积函数
• 换积分元素
• 换上下限

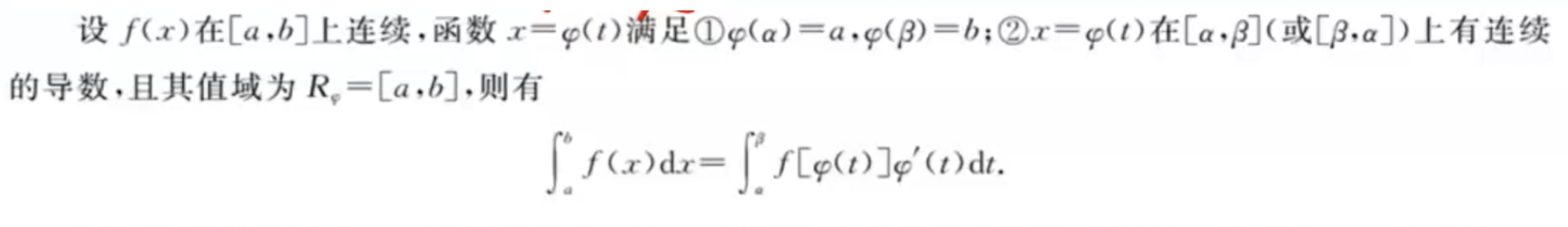
「定积分」换元积分法（六大换元法）

• 六大换元法

三角代换

三角函数常见换元公式

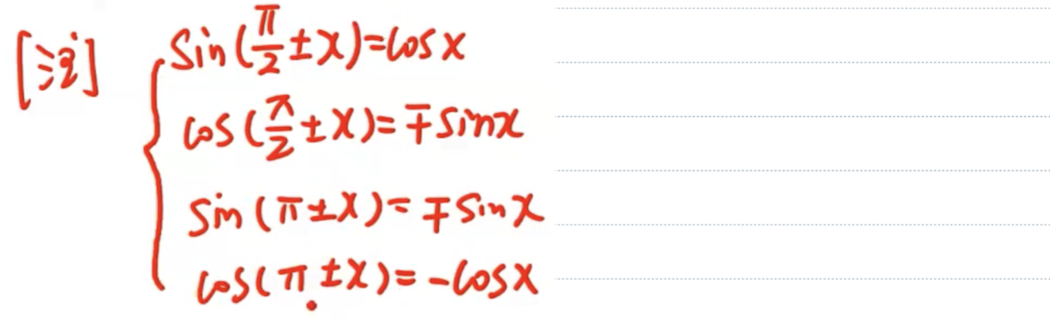
• 根式代换
• 倒代换
• 万能代换
• 整体代换
• 区间再现公式
  • 

「定积分」分部积分法

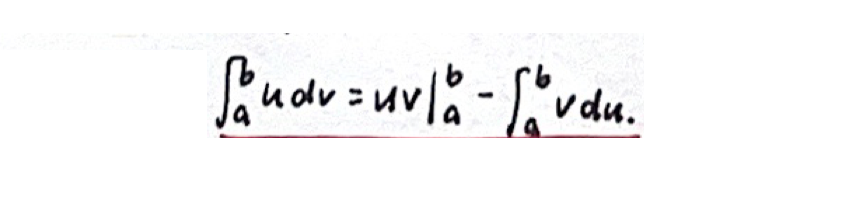
分部积分法 容易求导的作u

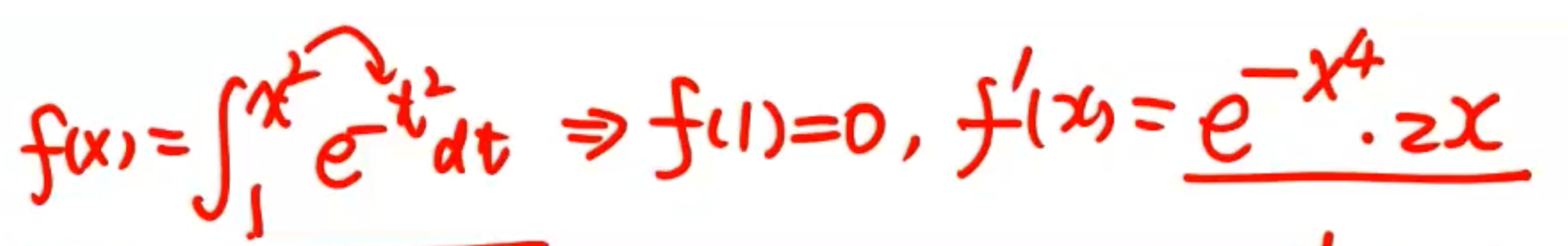
「定积分」利用奇偶性、周期性

「定积分」华里士公式

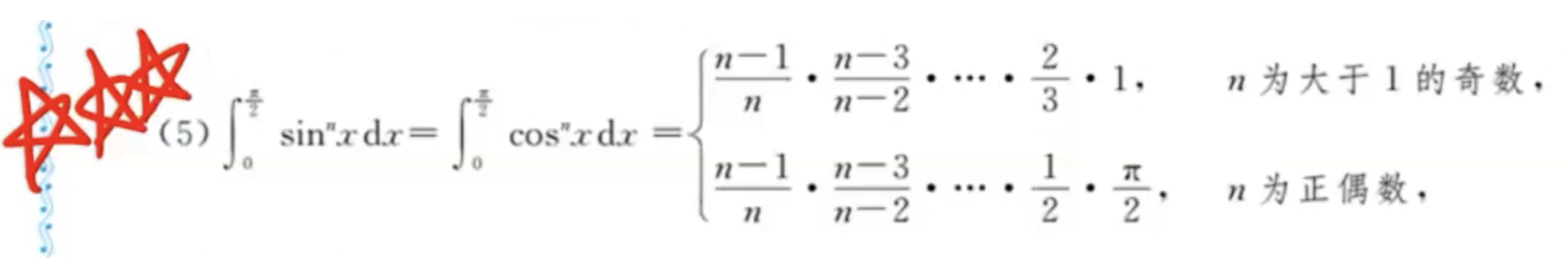
「定积分」华里士公式推论

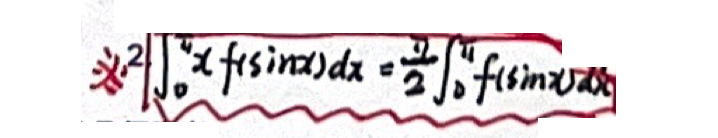
「定积分」华里士公式变形、区间为(2, 2n）

• ${\sin }^{n}x$ 以 $2\pi$ 为周期

• ${\cos }^{n}x$ 以 $2\pi$ 为周期

「定积分」华里士公式大全

变限积分的概念

变限积分的性质

变限积分性质证明

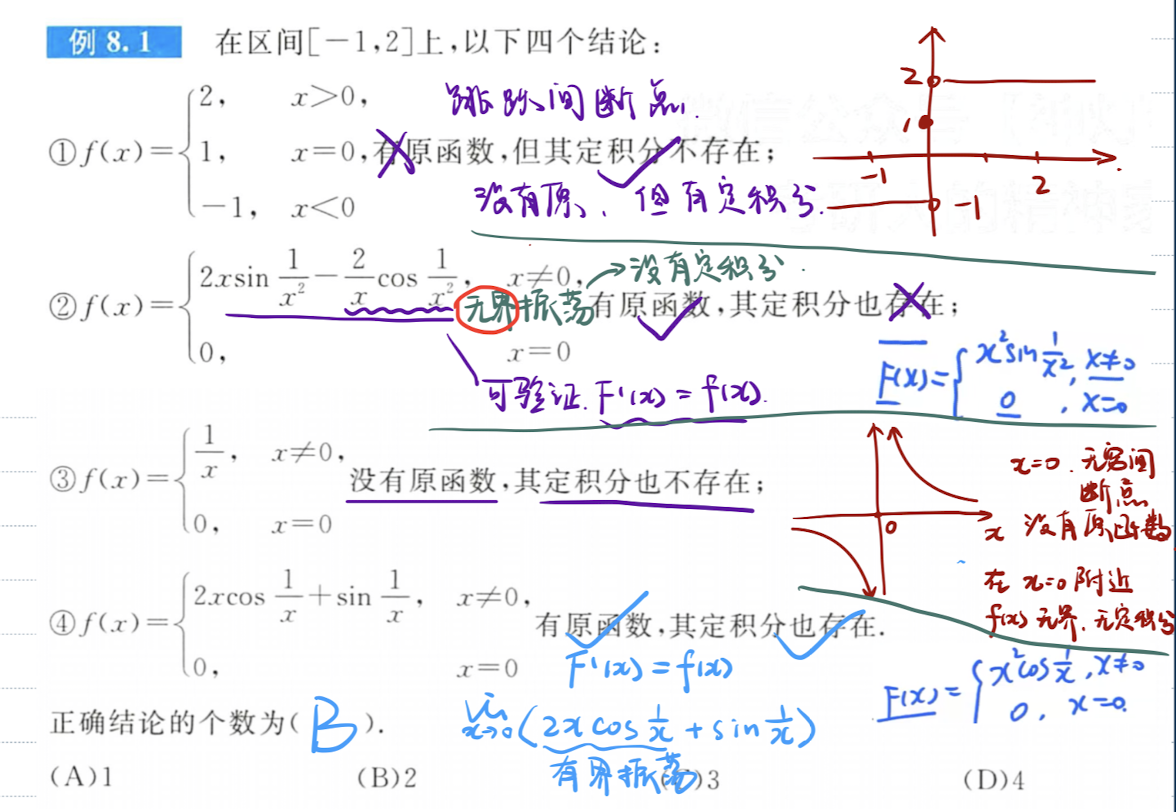
「题」没有原函数的函数积分图像

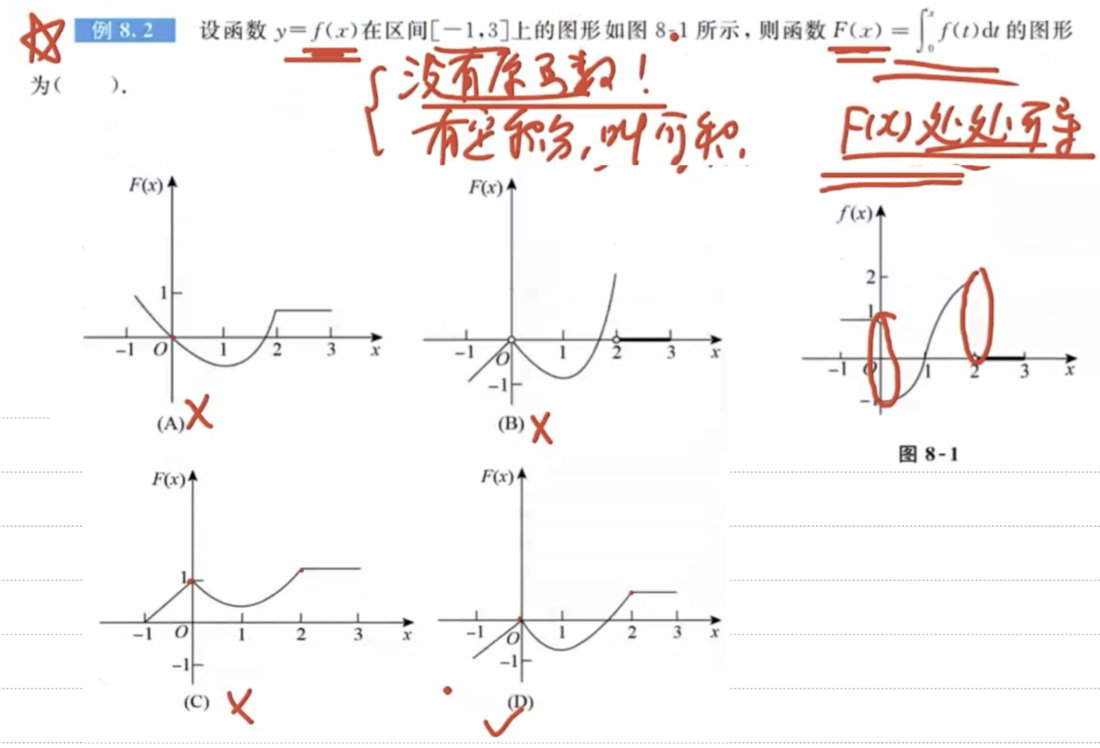
函数连续与原函数、变限积分的关系

变限积分的求导公式

「变上限积分」两种题型

「变上限积分」极限的求法