第八节导数应用

「极值」驻点的定义

驻点的定义

$y = f (x)$ 在 $x_{0}$ 邻域有定义，对 $\forall x$ ，恒有
- $f (x) \leq f (x_{0}) (f (x) \geq f (x_{0}))$
- $f^{'} (x_{0}) = 0$
的点称为驻点。

「极值」极值点的必要条件

使用费马定理可以证明该必要条件

设 $f (x)$ 在 $x = x_{0}$ 处可导，且在点 $x_{0}$ 处取得极值，则必有 $f^{'} (x_{0}) = 0$ 。

极值点和驻点并不相同

极值点 $\neq$ 驻点，可得极值点
- $f (x) = 0$
- $f (x)$ 不存在
可导 + 极值点 = 驻点

「极值」第一充分条件

设 $f (x)$ 在 $x = x_{0}$ 处连续，且在 $x_{0}$ 的某去心邻域 $\overset{˚}{U} (x_{0}, δ) (δ > 0)$

$f (x)$ 在 $x = x_{0}$ 取得	左邻域 $x \in (x_{0} - δ, x_{0})$	右邻域 $x \in (x_{0}, x_{0} + δ)$	是否变号
极小值	$f^{'} (x_{0}) < 0$	$f^{'} (x_{0}) > 0$	变
极大值	$f^{'} (x_{0}) > 0$	$f^{'} (x_{0}) < 0$	变
不是极值点	$f^{'} (x_{0}) > 0$	$f^{'} (x_{0}) > 0$	不变
不是极值点	$f^{'} (x_{0}) < 0$	$f^{'} (x_{0}) < 0$	不变

「极值」第二充分条件

$f^{'} (x_{0}) = 0, f^{″} (x_{0}) \neq 0$

$y = f (x)$ 在 $x_{0}$ 二阶可导
- $f^{'} (x_{0}) = 0, f^{″} (x_{0}) < 0$ 为极大值点
- $f^{'} (x_{0}) = 0, f^{″} (x_{0}) > 0$ 为极小值点
- $f^{″} (x_{0}) = 0$ 无法判定

证明极值第二充分条件

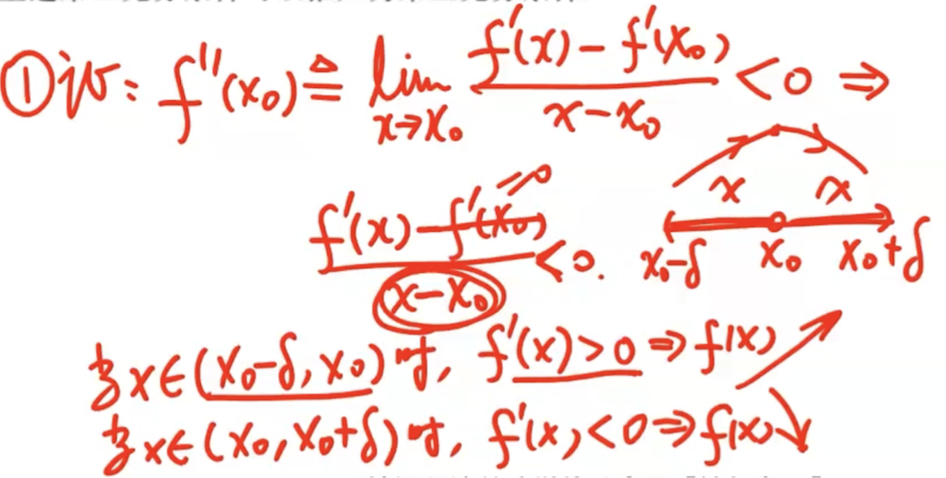
「极值」第三充分条件

高阶导数与极大值极小值

「极值」广义极值、去心邻域、定义一

$x_{0}$ 邻域内任意一点的函数值均小于等于该点的函数值

「极值」真正极值、去心邻域、定义二

$x_{0}$ 的某个去心邻域内任意一点的函数值均小于该点的函数值

「最值」定义

函数的最大值与最小值

$y = f (x)$ 在闭区间 $[a, b]$ 上有定义， $x_{0} \in [a, b]$ 对于任意 $x \in [a, b]$ ，恒有 $f (x) \in f (x_{0})$ ，称 $f (x_{0})$ 为在 $[a, b]$ 上的最大值

「最值」求法

函数最值求法

「最值」广义最值、定义域、定义三

$x_{0}$ 定义域内任意一点的函数值均小于等于该点的函数值

「最值」真正最值、定义域、定义四

$x_{0}$ 定义域内异于 $x_{0}$ 的任意一点的函数值均小于该点的函数值

「最值」求闭区间连续函数的最值

「步骤」1.驻点、不可导点 2.求端点 3.比较

「最值」求开区间连续函数的最值

「步骤」1.驻点、不可导点 2.求端点单侧极限 3.比较

「极值与最值」极值和最值的关系

最值点不一定是极值点，极值点不一定是最值点

极值点存在的前提是双侧有定义

最值点不一定是极值点
极值点不一定是最值点

「间断与极值」间断点也可以是极值点

分段函数中的间断点与极值点

「单调性」定理

$y = f (x)$	$f^{'} (x)$	$f (x)$
区间 $I$ 上	$f^{'} (x) > 0$	严格单增
区间 $I$ 上	$f^{'} (x) < 0$	严格单减

「凹凸性」定理

$y = f (x)$ 在 $[a, b]$ 连续，在 $(a, b)$ 二阶可导

$f (x)^{″}$	$f (x)^{″} > 0$	$f (x)^{″} < 0$
凹凸性	凹	凸
函数	$f (\frac{x_{1} + x_{2}}{2}) > \frac{f (x_{1}) + f (x_{2})}{2}$	$f (\frac{x_{1} + x_{2}}{2}) < \frac{f (x_{1}) + f (x_{2})}{2}$
图像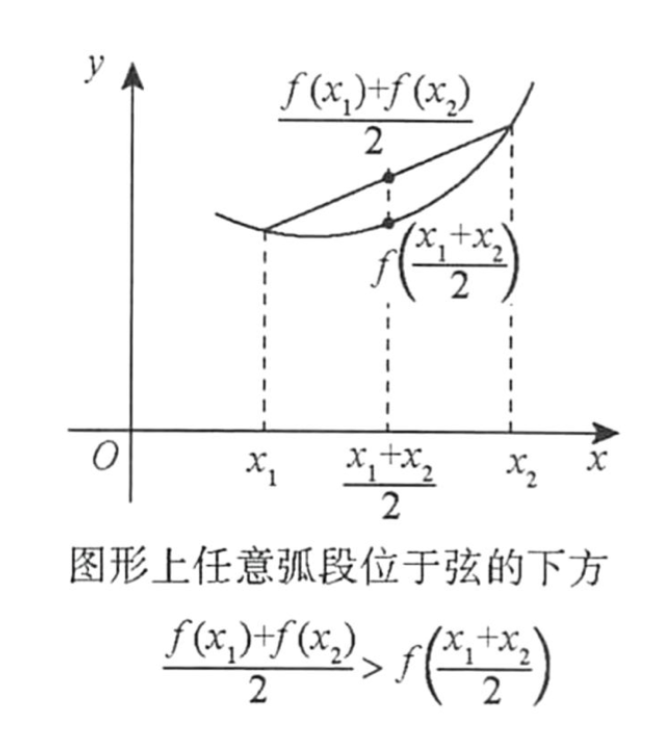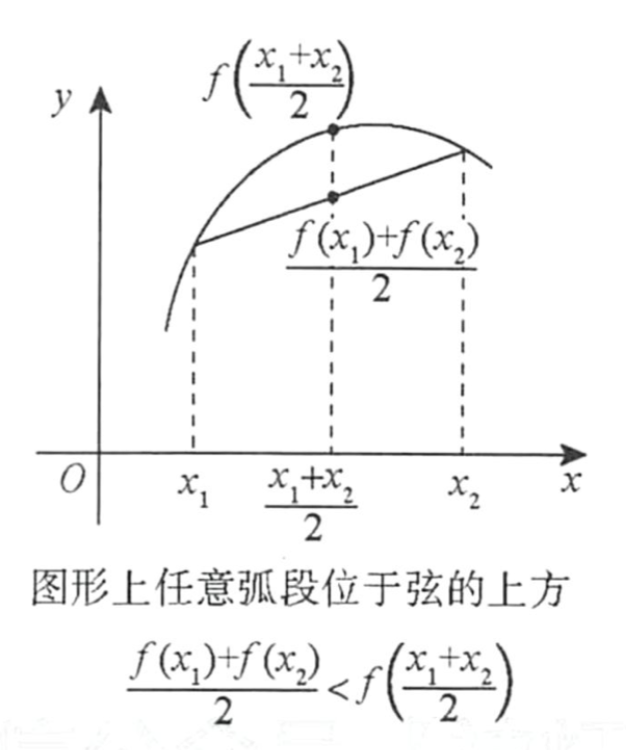

凹凸性的快速辨别

「拐点」定义

INFO

连接曲线的凹弧与凸弧的分界点称为该曲线的拐点。
- 拐点处只需连续
- 凹凸不分先后
- 拐点在曲线上，写 $(x_{0}, f (x_{0}))$

「拐点」必要条件

INFO

$f (x)$ 在 $x_{0}$ 处二阶可导，点 $(x_{0}, f (x_{0}))$ 为 $y = f (x)$ 的拐点，则 $f^{″} (x_{0}) = 0$ 。

「拐点」第一充分条件

「判断拐点」一阶连续，二阶导存在，左右邻域二阶导变号

「拐点」第二充分条件

「判断拐点」三阶可导，二阶导为零

「拐点」第三充分条件

「判断拐点」n 阶可导，m 阶导为零，n 阶导不为零，n 为奇数

第三充分条件不需要一阶导为 0

「渐近线」定义

水平渐近线、垂直渐近线、斜渐近线

渐近线判别顺序（铅>水>斜）

A111.高等数学

A112.线性代数

A113.概率论与数理统计

A212.C++

A214.Swift

A221.数据结构

A222.计算机组成原理

A223.计算机操作系统

A224.计算机网络

1231.常见算法

第八节导数应用

「极值」驻点的定义

「极值」极值点的必要条件

「极值」第一充分条件

「极值」第二充分条件

「极值」第三充分条件

「极值」广义极值、去心邻域、定义一

「极值」真正极值、去心邻域、定义二

「最值」定义

「最值」求法

「最值」广义最值、定义域、定义三

「最值」真正最值、定义域、定义四

「最值」求闭区间连续函数的最值

「最值」求开区间连续函数的最值

「极值与最值」极值和最值的关系

「间断与极值」间断点也可以是极值点

「单调性」定理

「凹凸性」定理

「拐点」定义

「拐点」必要条件

「拐点」第一充分条件

「拐点」第二充分条件

「拐点」第三充分条件

「渐近线」定义

「弧微分与曲率」定义

「方程实根」证明

「函数图像」作函数图像步骤 ⭐️

第八节 导数应用 ​

「极值」驻点的定义 ​

「极值」极值点的必要条件 ​

「极值」第一充分条件 ​

「极值」第二充分条件 ​

「极值」第三充分条件 ​

「极值」广义极值、去心邻域、定义一 ​

「极值」真正极值、去心邻域、定义二 ​

「最值」定义 ​

「最值」求法 ​

「最值」广义最值、定义域、定义三 ​

「最值」真正最值、定义域、定义四 ​

「最值」求闭区间连续函数的最值 ​

「最值」求开区间连续函数的最值 ​

「极值与最值」极值和最值的关系 ​

「间断与极值」间断点也可以是极值点 ​

「单调性」定理 ​

「凹凸性」 定理 ​

「拐点」定义 ​

「拐点」必要条件 ​

「拐点」第一充分条件 ​

「拐点」第二充分条件 ​

「拐点」第三充分条件 ​

「渐近线」定义 ​

「弧微分与曲率」定义 ​

「方程实根」证明 ​

「函数图像」作函数图像步骤 ⭐️ ​

第八节导数应用

「极值」驻点的定义

「极值」极值点的必要条件

「极值」第一充分条件

「极值」第二充分条件

「极值」第三充分条件

「极值」广义极值、去心邻域、定义一

「极值」真正极值、去心邻域、定义二

「最值」定义

「最值」求法

「最值」广义最值、定义域、定义三

「最值」真正最值、定义域、定义四

「最值」求闭区间连续函数的最值

「最值」求开区间连续函数的最值

「极值与最值」极值和最值的关系

「间断与极值」间断点也可以是极值点

「单调性」定理

「凹凸性」定理

「拐点」定义

「拐点」必要条件

「拐点」第一充分条件

「拐点」第二充分条件

「拐点」第三充分条件

「渐近线」定义

「弧微分与曲率」定义

「方程实根」证明

「函数图像」作函数图像步骤 ⭐️