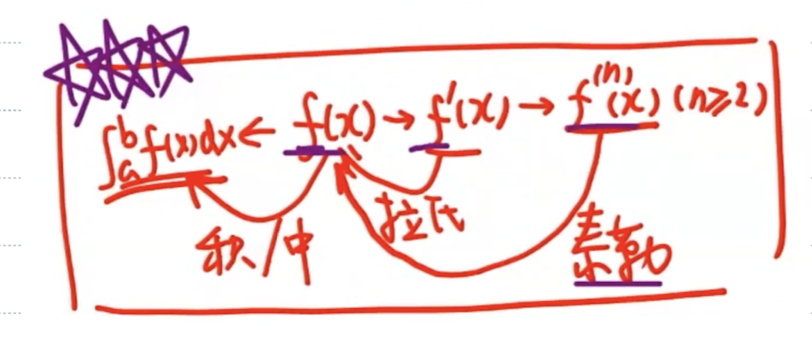
第七节 微分中值定理

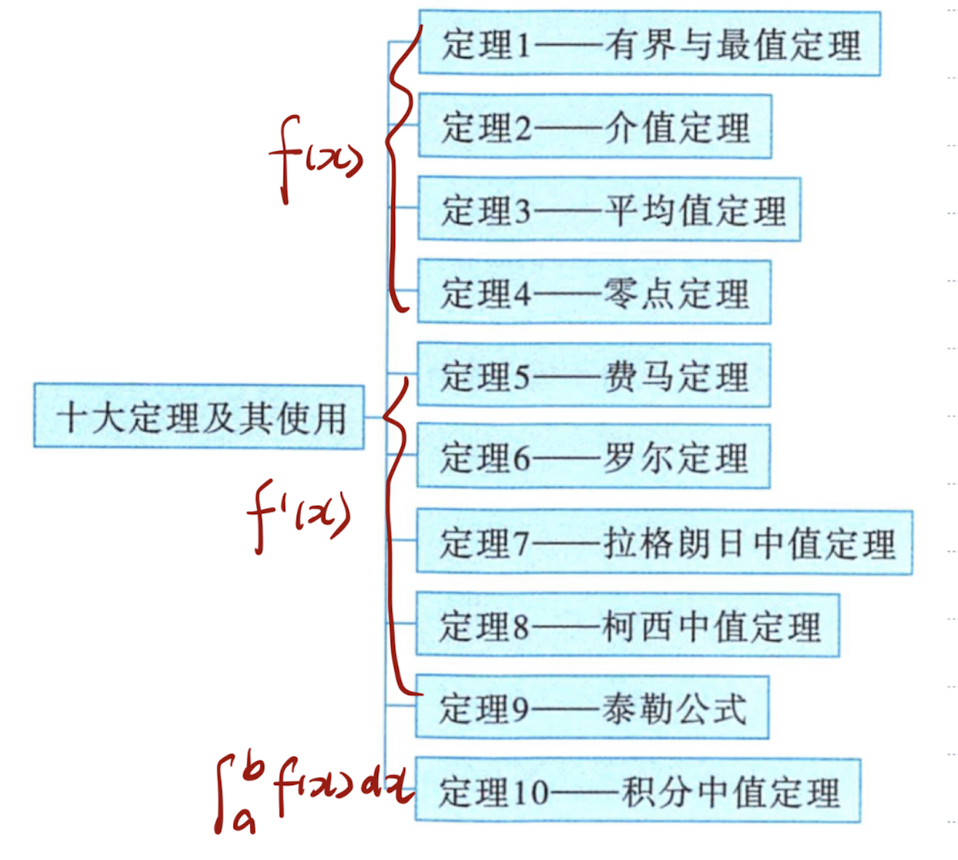
「函数」有界与最值定理

INFO

• 设 $f(x)$ 在 $[a,b]$ 上连续，则 $m\le f(x)\le M$，其中 $m,M$ 分别为 $f(x)$ 在 $[a,b]$ 上的最小值与最大值

「函数」介值定理

INFO

• 设 $f(x)$ 在 $[a,b]$ 上连续，则 $m\le \mu \le M$，存在 $\xi \in [a,b]$，使得 $f(\xi )=\mu$

「函数」平均值定理

INFO

• 当 $a<x_1<x_2<\cdots <x_n<b$ 时，在 $[x_1,x_n]$ 内至少存在一点 $\xi$，使

$$f(\xi )=\frac{f(x_1)+f(x_2)+\cdots +f(x_n)}{n}$$

「分析」最值+介值

「函数」零点定理

• 零点定理是介值定理的推论
• 主要用于证明根的存在性

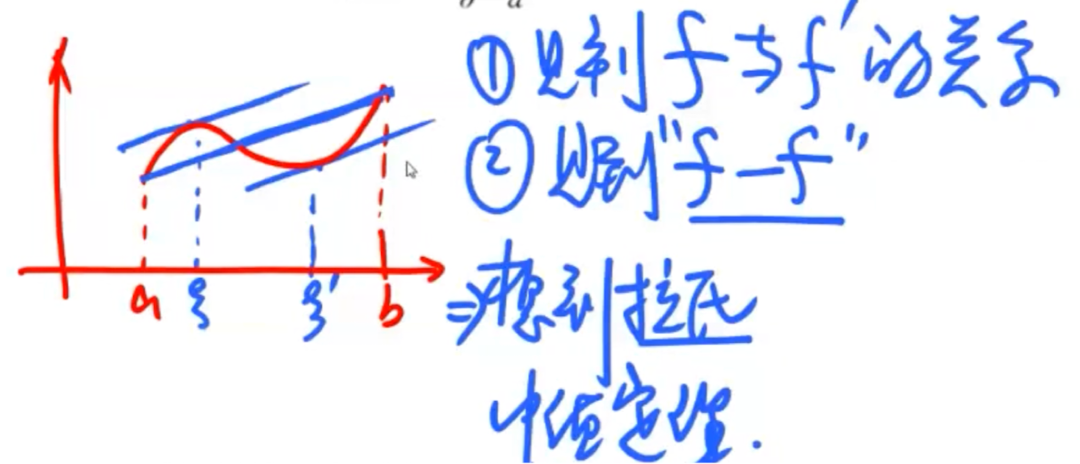
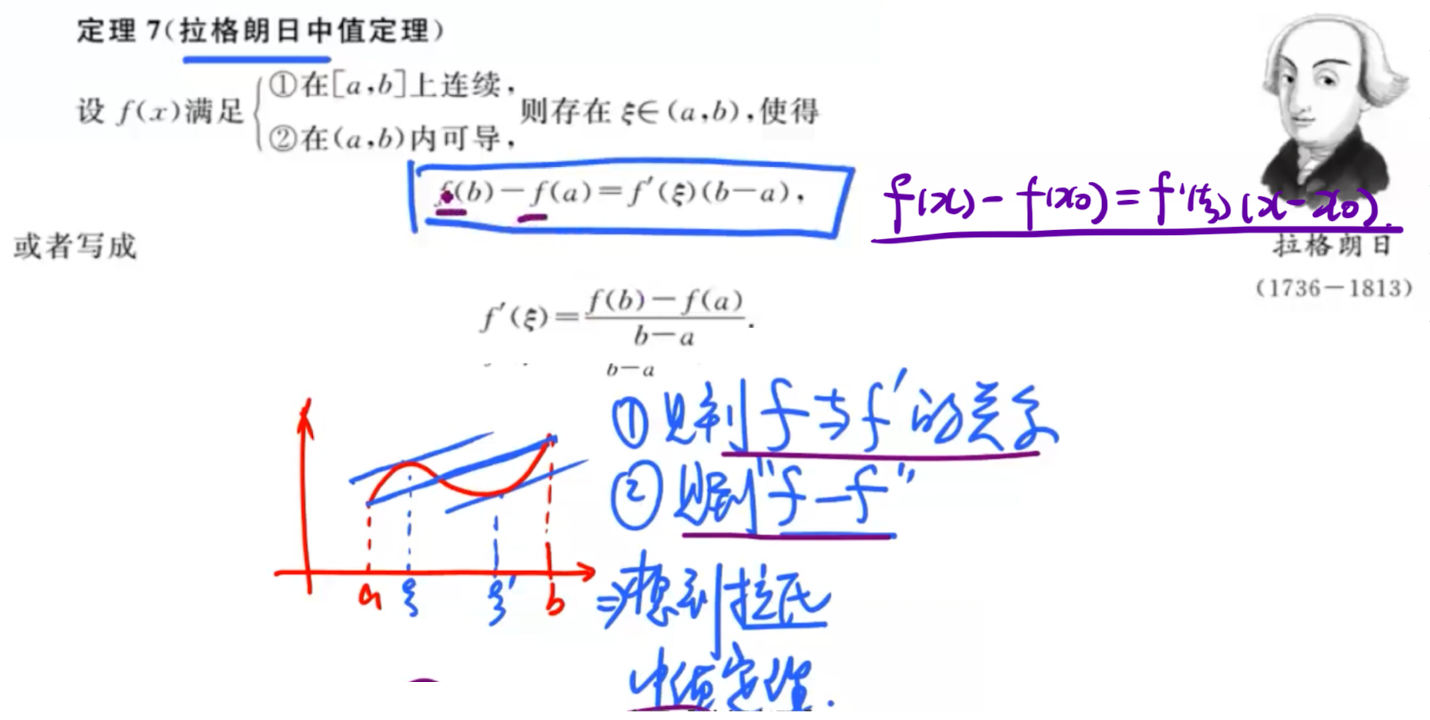
「函数」拉格朗日中值定理

见到「f与f'」&「f-f」就要想到拉格朗日中值定理

「函数」积分中值定理

INFO

• 设 $f(x)$ 在 $[a,b]$ 上连续，证明存在 $\xi \in [a,b]$，使得

$${\displaystyle {\int }_a^{b}f(x)dx=f(\xi )(b-a)}$$

「分析」最值+介值

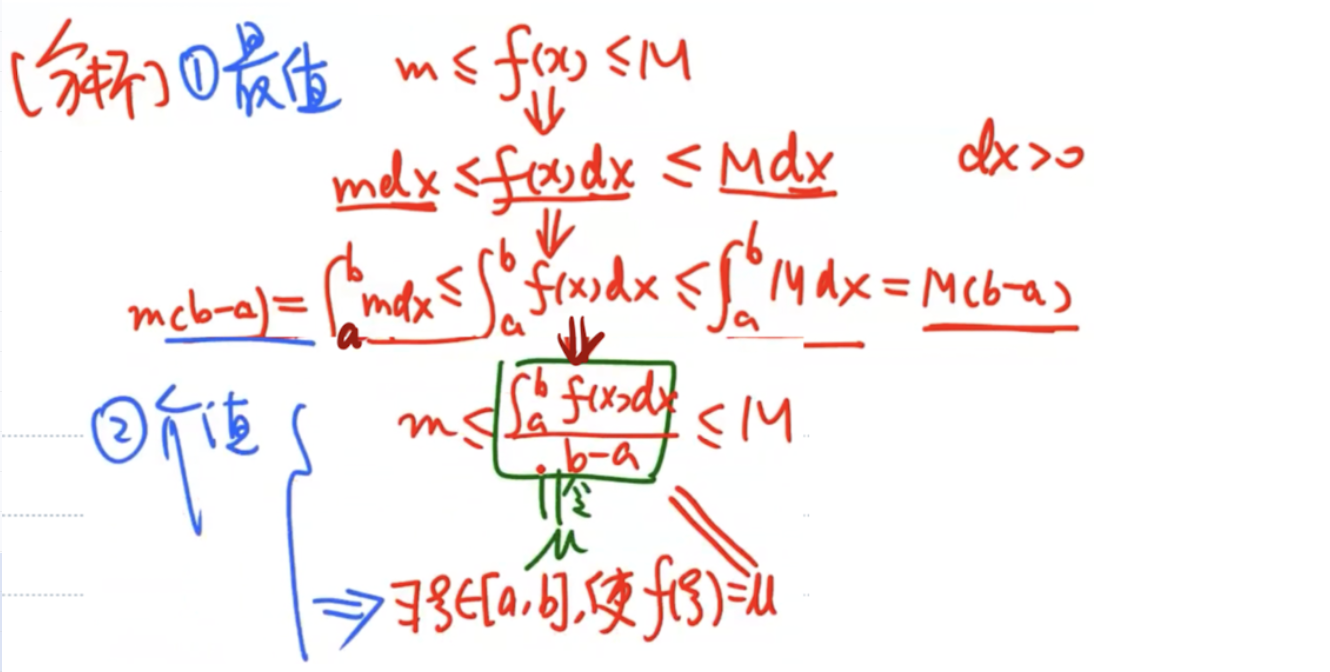
积分中值定理 = 连续的平均值定理

用拉格朗日证明积分中值定理

• 设 $f(x)$ 在 $[a,b]$ 上连续，证明存在 $\xi \in [a,b]$，使得

$${\displaystyle {\int }_a^{b}f(x)dx=F(b)-F(a)=f(\xi )(b-a)}$$

「导数」费马定理

脱帽法与戴帽法

费马定理的应用（导数零点定理）

导数零点定理和零点定理的不同

「导数」罗尔定理

罗尔定理的推广（直接用，不用证明）

罗尔定理的使用（构造辅助函数）

「导数」拉格朗日中值定理

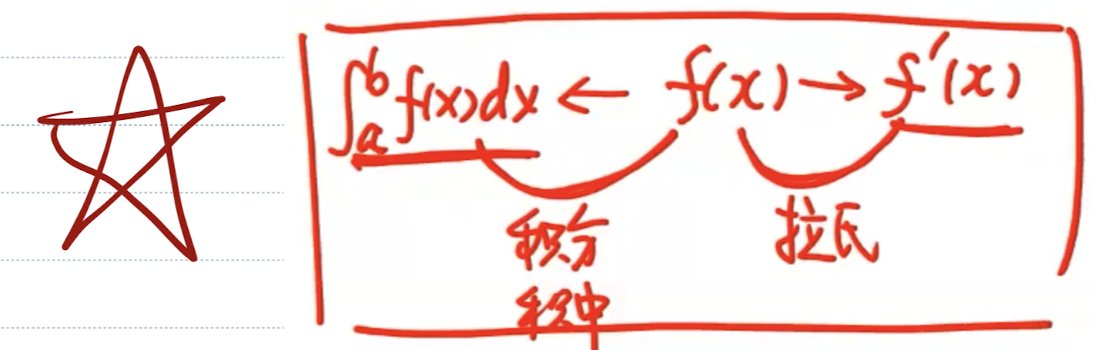
积分、函数、导数之间的桥梁

「导数」柯西中值定理

「中值定理」三大中值定理的意义

• 建立函数与导数之间的关系

「泰勒公式」皮亚诺余项

研究局部形态，极限、极值

• 带佩亚诺余项的 $n$ 阶泰勒公式
  • 设 $f(x)$ 在点 $x_0$ 处 $n$ 阶可导，则存在 $x_0$的一个邻域（局部上），对于邻域内的任一点 $x$，有

$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{1}{2!}{f}^{″}(x_0)(x-x_0{)}^2+\cdots +\frac{1}{n!}{f}^{(n)}(x_0)(x-x_0{)}^n+o[(x-x_0{)}^n]$$

• 常称 $R_n(x)=o[(x-x_0{)}^n]$ 为佩亚诺余项
• 若 $x_0=0$ 得麦克劳林公式

「泰勒公式」拉格朗日余项

研究整体形态，最值、不等式

「泰勒公式」皮亚诺、拉格朗日的异同点

皮亚诺、拉格朗日 的异同点	共同点	不同点
	多项式逼近	条件不同
	联系函数与高阶导数	余项不同

「泰勒公式」麦克劳林公式

「泰勒公式」麦克劳林展开式

「⭐️」各阶导数之间的联系