第二节 极限

「数列极限」定义 & NOTE

数列极限	解释
定义	$\mathrm{\forall }ϵ>0,N\in N_{+}(\mathrm{正}\mathrm{整}\mathrm{数})，n>N$，恒有 ${\displaystyle |X_n-a|<ϵ\iff \underset{n\to \mathrm{\infty }}{lim}{X}_n=a}$
注意事项	1. $ϵ$ 刻画 $X_n$ 与 $a$ 的接近程度，$N$ 刻画 $n\to \mathrm{\infty }$ 的过程 2. ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}{X}_n=a}$ 的几何意义，为 在 $(a-ϵ,a+ϵ)$ 存在 $N$，使 $n>N$ ，使 $X_n$ 落在 $(a-ϵ,a+ϵ)$ ，只有有限个在区间之外 3. $X_n$ 存在，极限存在，极限值等于多少与数列前有限项无关 4. ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}{X}_n=a\iff \underset{k\to \mathrm{\infty }}{lim}{X}_{2k-1}=\underset{k\to \mathrm{\infty }}{lim}{X}_{2k}=a}$

「数列极限」夹逼准则

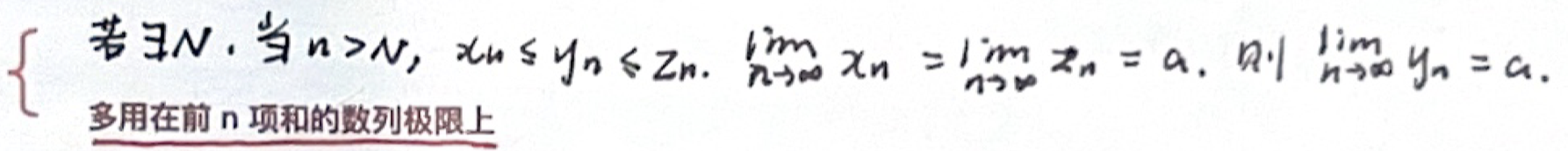
「数列极限」单调有界准则

INFO

• 单调有界数列必有极限
  • 单增（单减）有上（下）界的数列必有限

TIP

单调有界准则多用在求递推关系式 $X_{n+1}=f(x_n)$ 所定义的数列极限上，函数也有这两条准则

「数列极限」收敛数列的性质

收敛数列
性质
唯一性 有界性	如若数列极限存在，则可以推断极限唯一并且数列有界
保号性 脱帽法 戴帽法	脱帽、戴帽指的是极限符号 脱帽法 数列存在极限，且极限大于0，则数列在N后的任何元素均大于0 ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}{X}_n=a>0\Rightarrow n>N,X_n>0}$ 戴帽法 数列任何元素均大于等于0，数列存在极限，则数列极限大于等于0 ${\displaystyle X_n\ge 0,\underset{n\to \mathrm{\infty }}{lim}{X}_n=a\Rightarrow a\ge 0}$

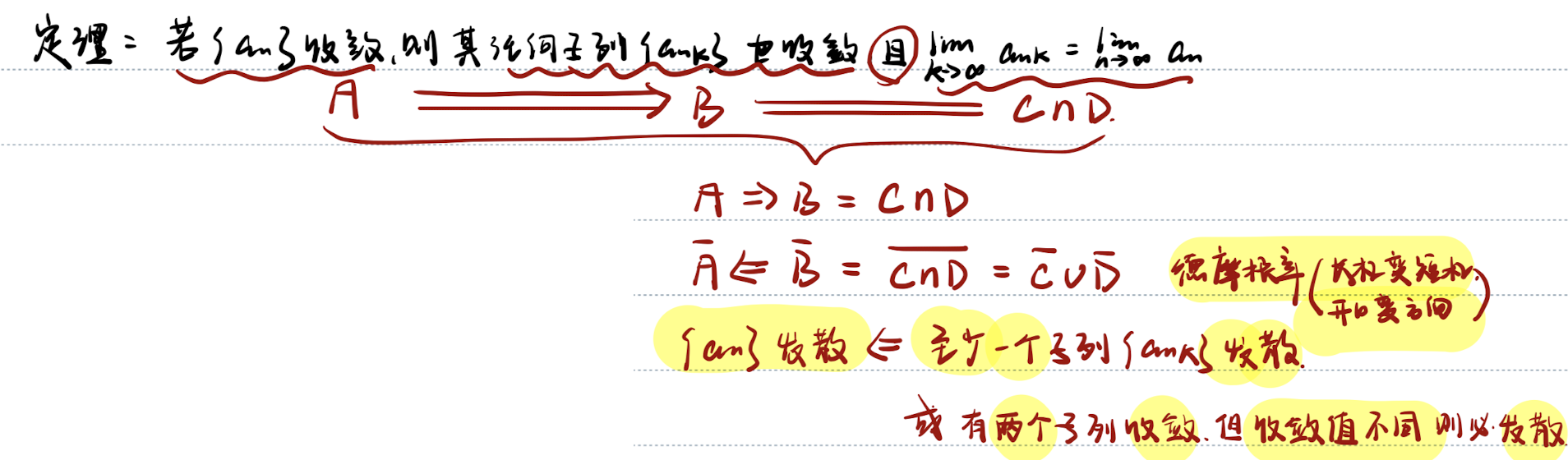
「数列的收敛与发散」性质 & 德摩根律

数列	子列
收敛	任何子列都收敛
发散	至少一个子列发散

德摩根律 表示 数列及其子列关系

「函数极限」自变量趋于有限值

$ϵ-\delta$ 语言	描述函数极限定义的数学语言
函数极限定义	$\mathrm{\forall }ϵ>0$，$\mathrm{\exists }\delta >0$，$0<|x-x_0|<\delta$，恒有${\displaystyle |f(x)-A|<ϵ}$，${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}f(x)=A}$
注意	$x\to x_0$，但是 $x\ne x_0$，要极限存在，必须使 $x=x_0$ 在去心邻域 $(x_0,\delta )$ 处处有定义
定理	极限存在的充要条件 是左极限与右极限存在且相等

「函数极限」自变量趋于无穷大

定义	解释
定义一	$ϵ>0,x>0,x>X$，恒有${\displaystyle |f(x)-A|<ϵ，\underset{x\to +\mathrm{\infty }}{lim}f(x)=A}$
定义二	$ϵ>0,x>0,x<-X$，恒有${\displaystyle |f(x)-A|<ϵ，\underset{x\to +\mathrm{\infty }}{lim}f(x)=A}$
定义三	$ϵ>0,x>0,|x|>X$，恒有${\displaystyle |f(x)-A|<ϵ，\underset{x\to +\mathrm{\infty }}{lim}f(x)=A}$
定理	极限存在的充要条件 是负无穷极限，正无穷极限存在并相等 ${\displaystyle [\underset{x\to \mathrm{\infty }}{lim}f(x)\mathrm{存}\mathrm{在}\iff \underset{x\to -\mathrm{\infty }}{lim}f(x)=\underset{x\to +\mathrm{\infty }}{lim}f(x)]}$

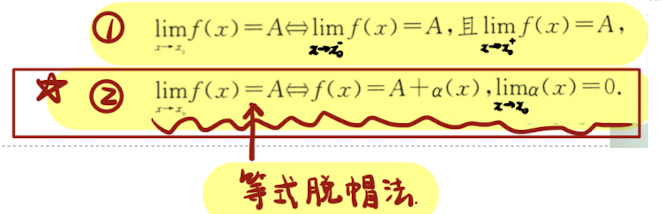
「函数极限」极限存在的充要条件

1. 左极限 = 右极限 = 极限值
2. 函数极限存在 $\iff$ 极限的无穷小的极限值为0
3. 等式脱帽法 就是 函数极限去掉极限符号，极限值加上无穷小。

「函数极限分左右」分段函数在分界点处

• 分界点两侧函数表达式不同（也包括带有绝对值的函数，如${\displaystyle \underset{x\to 0}{lim}\frac{|x|}{x}}$）

「函数极限分左右」e^无穷 型

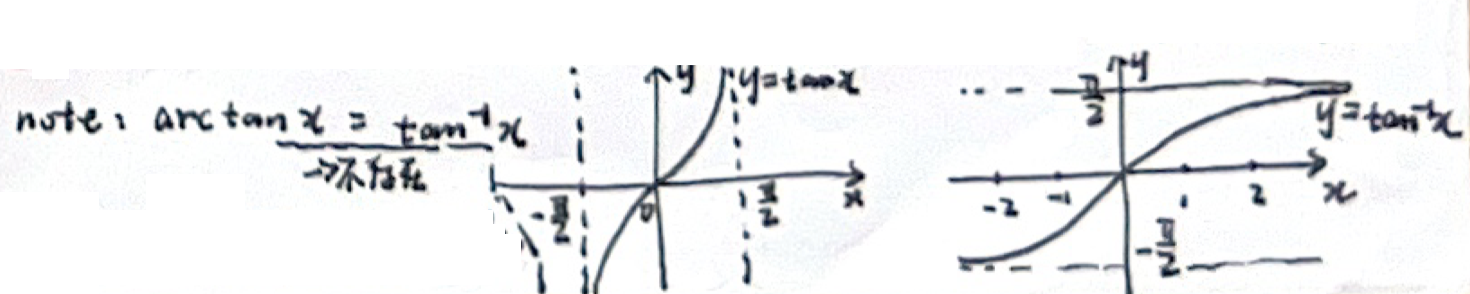
「函数极限分左右」arctan无穷 型

「极限性质」有界性

有界性	数列	函数
	收敛必有界（反之不成立） 无界必发散，发散不一定无界	函数极限存在，函数在 $x_0$ 的去心邻域内有界，即局部有界（反之不成立）
反例	$x_n=(-1{)}^n$，有界不收敛	${\displaystyle f(x)=\sin \frac{1}{x}}$，$x=0$ 去心邻域有界，但 ${\displaystyle \underset{x\to 0}{lim}\sin \frac{1}{x}}$ 无界

「极限性质」保号性

保号性
数列
函数

为什么 $A\ge 0$，不能推出 $X_n\ge 0$ 呢？

• 因为极限取的是一个值，而数列取的是极限值周围的一个邻域，并不能保证数列大于等于0，可能会小于0。

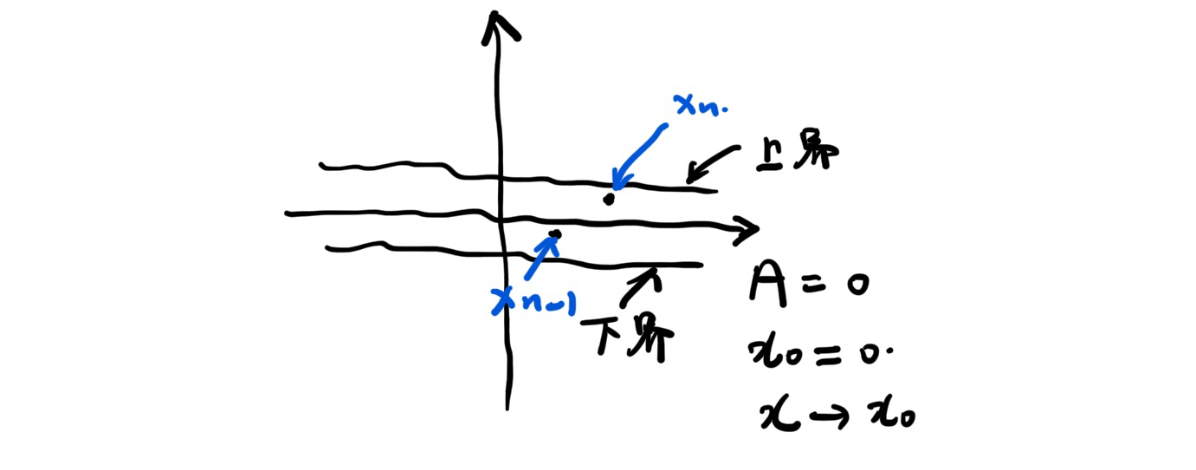
「极限性质」极限值与无穷之间的关系

• $limf(x)=A\iff f(x)=A+\alpha (x)$，其中 $lim\alpha (x)=0$

「无穷小量」无穷小的比阶

注意：并不是任意两个无穷小都可以比阶

「无穷小量」无穷小的性质

运算数	运算	结果
有限个 无穷小	和	无穷小
有限个 无穷小	积	无穷小
无穷小 与 有界变量	积	无穷小

$$\underset{n\to \mathrm{\infty }}{lim}[\frac{1}{n^2}+\frac{2}{n^2}+\cdots +\frac{n}{n^2}]=\underset{n\to \mathrm{\infty }}{lim}\frac{\frac{1}{2}n(n+1)}{n^2}=\frac{1}{2}$$

无穷小的四则运算	四则运算表达式
加减法时，低阶吸收高阶	$O(x^m)\pm O(x^n)=O(x^l)(l=min\{m,n\})$
乘除法时，阶数累加	$O(x^m)\cdot O(x^n)=O(x^{m+n})$ $x^m\cdot O(x^n)=O(x^{m+n})$
常数乘不影响阶数	$O(x^m)=O(k{x}^m)=k\cdot O(x^m)$

「无穷小量」常用等价无穷小

• 当 $x\to 0$ 时，常用的等价无穷小
  • $sinx\sim x$，$tanx\sim x$，$arctanx\sim x$
  • $ln(1+x)\sim x$，$e^x-1\sim x$
  • $a^x-1\sim xlna$，${\displaystyle 1-cosx\sim \frac{1}{2}{x}^2}$
  • $(1+x{)}^{\alpha }-1\sim \alpha x$

「无穷大量」常用无穷大量的比较

趋向	无穷大量的比较
$x\to +\mathrm{\infty }$	$l{n}^{\alpha }x<<x^{\beta }<<a^x(\alpha >0,\beta >0,a>0)$ 可用洛必达证明
$n\to \mathrm{\infty }$	$l{n}^{\alpha }n<<n^{\beta }<<a^n<<n!<<n^n(\alpha >0,\beta >0,a>0)$

「无穷大量」无穷大量的性质

$$\mathrm{无}\mathrm{穷}\mathrm{大}\mathrm{量}+\mathrm{无}\mathrm{穷}\mathrm{大}\mathrm{量}=\mathrm{无}\mathrm{穷}\mathrm{大}\mathrm{量}$$$$\mathrm{无}\mathrm{穷}\mathrm{大}\mathrm{量}+\mathrm{有}\mathrm{界}\mathrm{变}\mathrm{量}=\mathrm{无}\mathrm{穷}\mathrm{大}\mathrm{量}$$$$\mathrm{无}\mathrm{穷}\mathrm{大}\mathrm{量}(n)\times \mathrm{有}\mathrm{界}\mathrm{变}\mathrm{量}(\frac{1}{n^2})\ne \mathrm{无}\mathrm{穷}\mathrm{大}\mathrm{量}(\frac{1}{n})$$

「无穷大量与无界变量」关系

「无穷大量与无穷小量」关系

无穷大量与无穷小量的关系

同一极限过程中，$f(x)$ 为无穷大，${\displaystyle \frac{1}{f(x)}}$ 为无穷小，反之亦然 $f(x)\ne 0$。

「无穷大量与无穷小量」七种未定式

序号	未定式
(i)	${\displaystyle \frac{0}{0}、\frac{\mathrm{\infty }}{\mathrm{\infty }}、\mathrm{\infty }\cdot 0}$
(ii)	${\displaystyle \mathrm{\infty }-\mathrm{\infty }}$
(iii)	${\displaystyle {\mathrm{\infty }}^0、0^0、1^{\mathrm{\infty }}}$

「海涅定理」归结原则

海涅定理的定义（去心邻域函数极限存在，数列极限存在）

• 设 $f(x)$ 在 $\mathring{U}(x_0,\delta )$ 内有定义，则 ${\displaystyle \underset{x\to x_0}{lim}f(x)=A}$ 存在 $\iff$ 对任何 $\mathring{U}(x_0,\delta )$ 内以 $x_0$ 为极限的数列 $\{x_n\}(x_n\ne x_0)$，极限 ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}f(x_n)=A}$ 存在。

海涅定理的作用

• 搭建起了函数极限和数列极限之间的桥梁

「海涅定理」使用

用于证明 ${\displaystyle \underset{x\to 0}{lim}\frac{1}{x}\sin \frac{1}{x}}$ 不存在

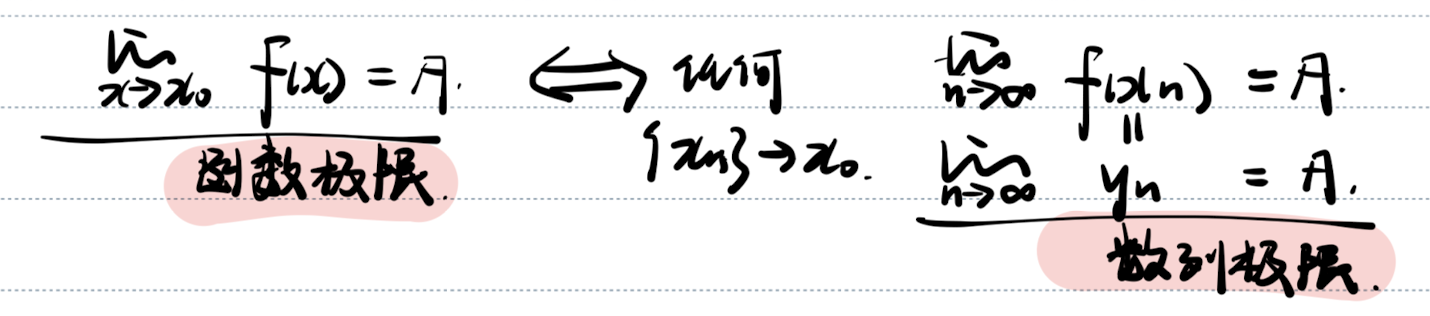
「海涅定理」考法

$\mathrm{左}\to \mathrm{右}$
$\mathrm{右}\to \mathrm{左}$

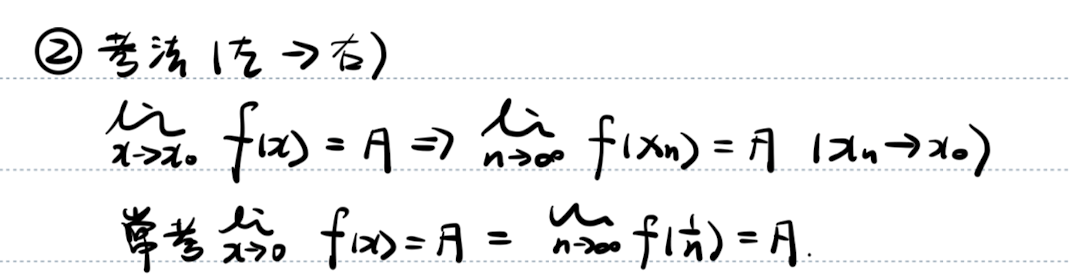「求极限」常用求极限的8种方法

「基本极限」两个重要极限

$$\underset{x\to 0}{lim}\frac{sinx}{x}=1$$$$\underset{x\to \mathrm{\infty }}{lim}(1+\frac{1}{x}{)}^x=e$$

「基本极限」极限常用公式

「基本极限」1^∞ 型极限 常用结论

「等价无穷小」替换原则

• 乘除关系可以换
• 加减关系在一定条件下可以换（$\alpha$ 与 $\beta$ 不等价）
  • 

「等价无穷小」常用公式（x->0时）

「有理运算法则」 函数极限

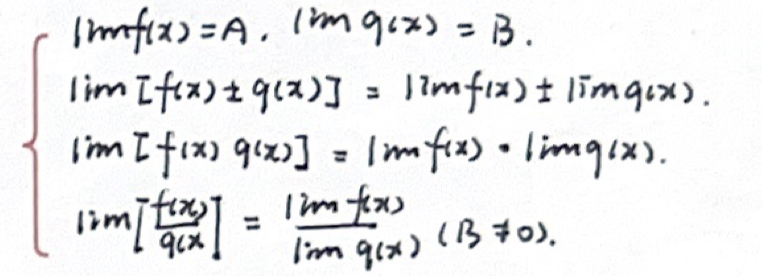
「有理运算法则」 存在与不存在的有理运算

「极限求解」极限中分子分母关系

「洛必达」使用条件

「洛必达」求七种不定式极限

「泰勒公式」皮亚诺余项

INFO

• $f(x)$ 在 $x=x_0$ 处 $n$ 阶可导，则

$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{″}(x_0)}{2!}(x-x_0{)}^2+\cdots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+o[(x-x_0{)}^n]$$

• 当 $x_0=0$ 时，

$$f(x)=f(0)+f^{\prime }(0)x+\frac{f^{″}(x_0)}{2!}{x}^2+\cdots +\frac{f^{(n)}(0)}{n!}{x}^n+o(x^n)$$

顺口溜

• 指对函数一二三
• 正弦函数一三五
• 正弦对数隔一换
• 正弦指数有感叹

「泰勒公式」常用公式

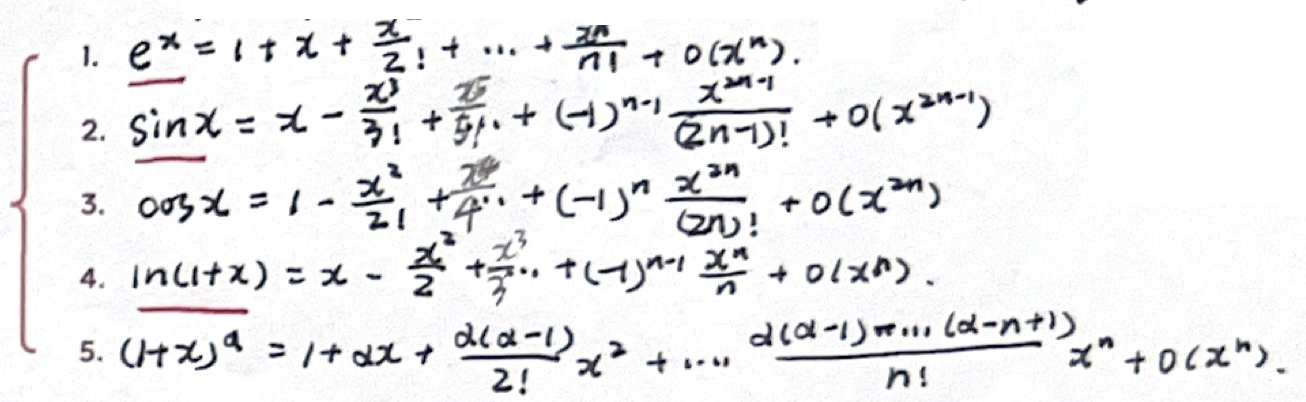
狗-sin狗

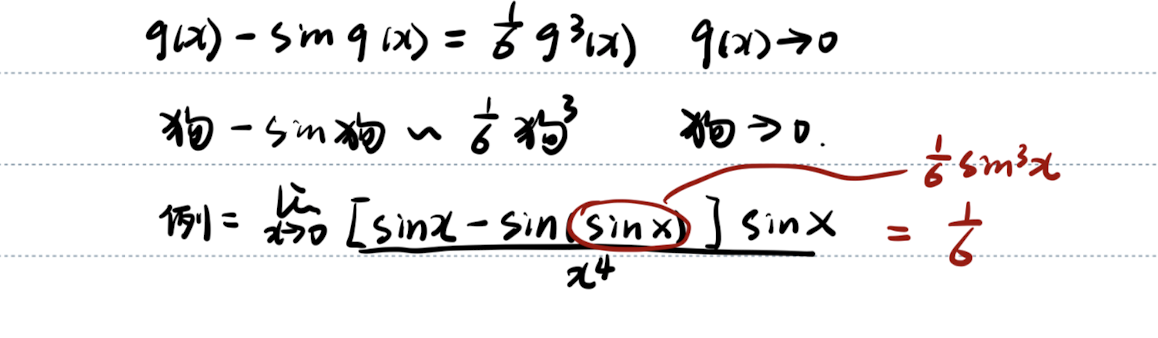
泰勒公式展开时，应该展开到几次幂？

1. $A/B$ 型，上下展开到同阶
2. $A-B$ 型，展开到系数不同，阶数相同的项

「夹逼定理」数列极限

「单调有界准则」数列极限

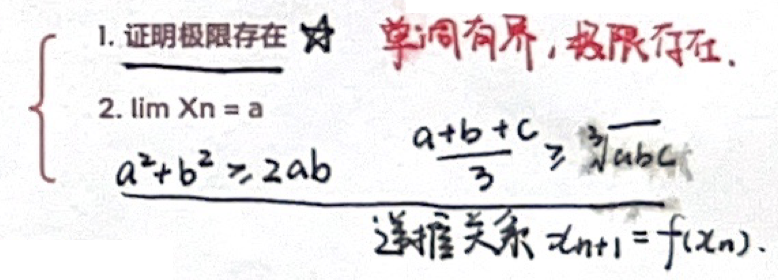
「定积分定义」数列极限（第五章）

• 定积分定义（黎曼）