第九节 不定积分

「原函数」性质

原函数
性质	设函数 $f(x)$ 定义在某区间 $I$ 上，若存在可导函数 $F(x)$，对于该区间上任意一点都有 $F(x)=f(x)$ 成立，则称 $F(x)$ 是 $f(x)$ 在区间 $I$ 上的一个原函数，称 ${\displaystyle \int F(x)dx=F(x)+C}$ 为 $f(x)$在区间 $I$ 上的不定积分
备注	全体原函数被称作不定积分

「原函数」存在定理

INFO

• $f(x)$ 在区间 $I$ 上连续，一定存在原函数。

  • 存在原函数的函数不一定连续。

• $f(x)$ 在区间 $I$ 上有第一类间断点，没有原函数。

  • 若存在第二类间断点，则不一定连续。

• $f(x)$ 为不连续函数

  • 有第一类间断点，没有原函数。
  • 有第二类间断点，不一定有没有原函数。

• 连续函数 $f(x)$ 必有原函数 $F(x)$

定理
证明

「原函数」间断点与原函数

• 若$F(x)$处处可导，$F^{\prime }(x)$为连续、振荡点
  • 含有第一类间断点（跳跃、可去）和无穷间断点的函数$f(x)$在包含该间断点的区间内没有原函数$F(x)$
  • 振荡间断点 可能有（有界振荡、${\displaystyle x^2\sin \frac{1}{x}}$)，也可能没有（无界振荡、${\displaystyle \frac{1}{x}\sin \frac{1}{x},x\ne 0}$）原函数$F(x)$

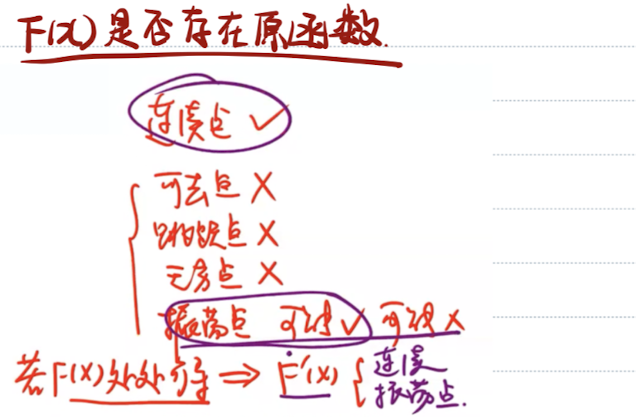
间断点	有无原函数	证明
可去间断点	🈚️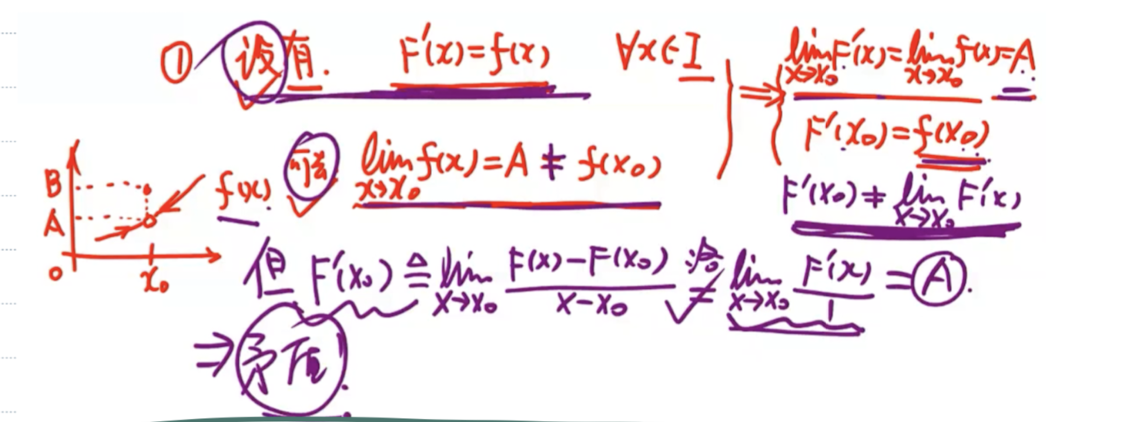
跳跃间断点	🈚️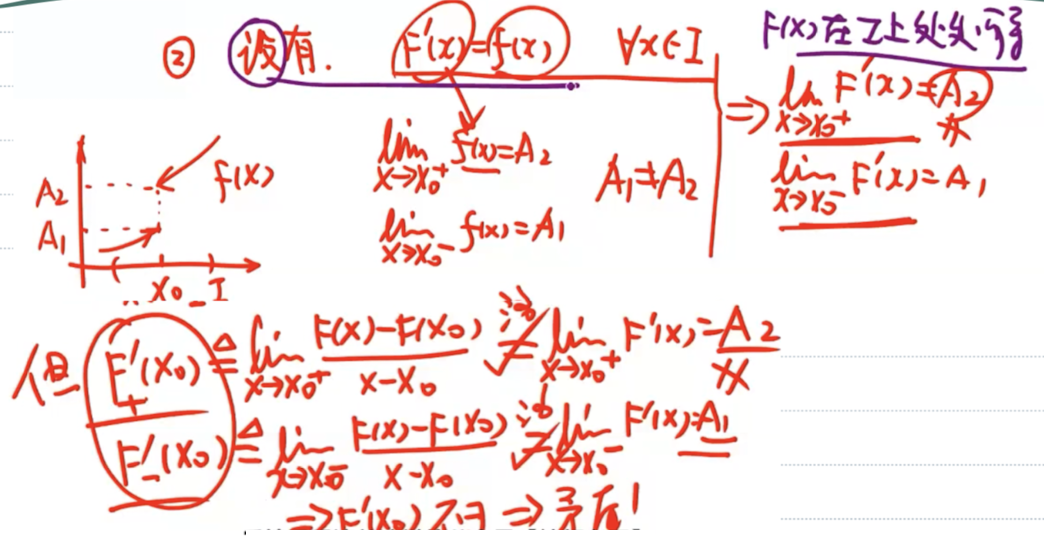
无穷间断点	🈚️
振荡间断点	可能有 可能没有

有无原函数	从介值定理理解函数是否会存在原函数
一定没有原函数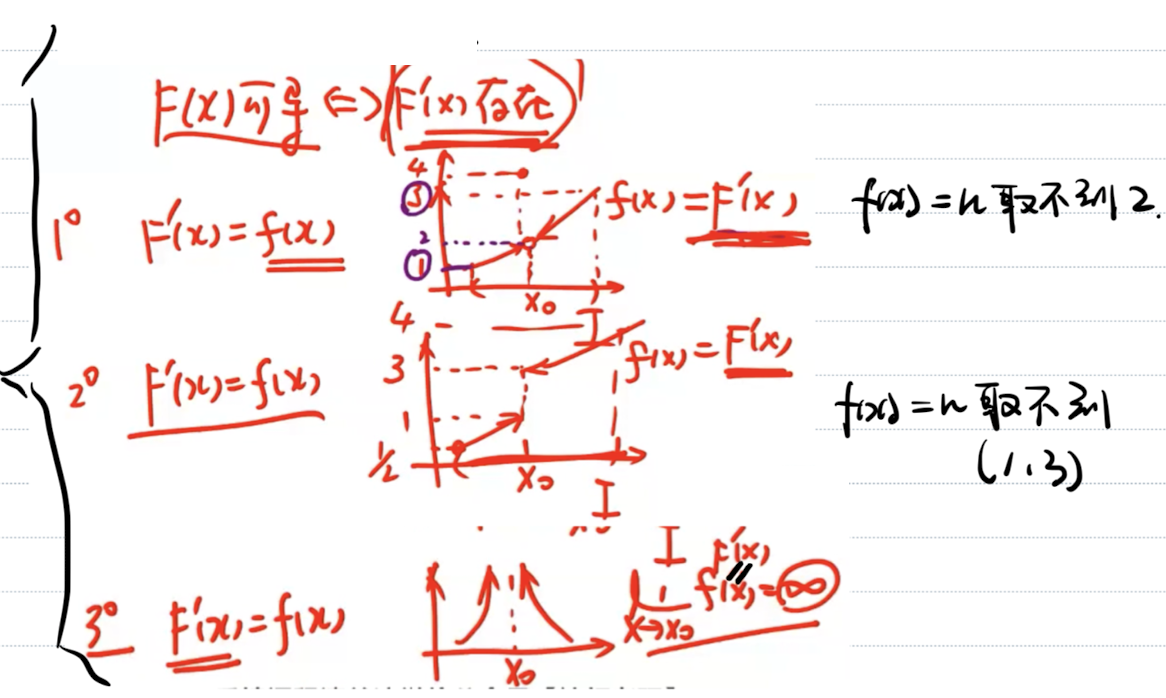
可能有、可能没有原函数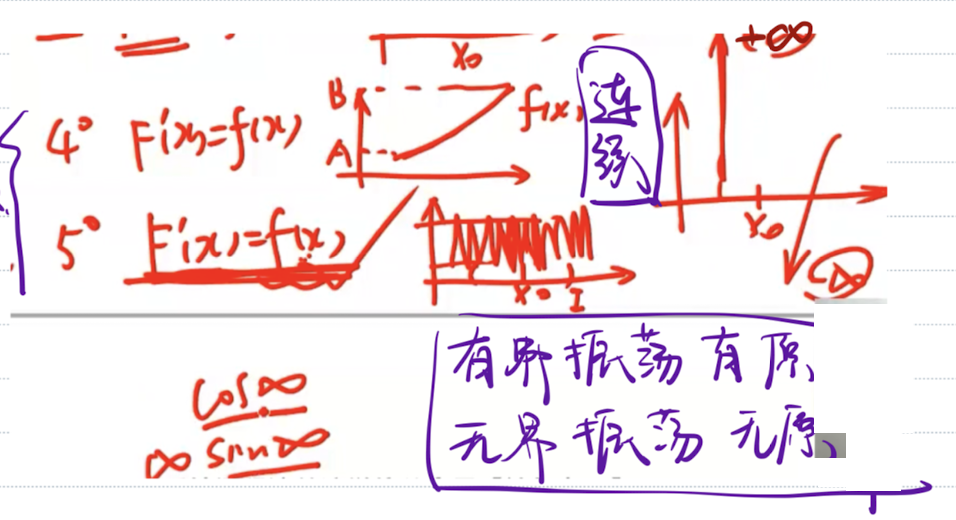

积分、函数、导数关系

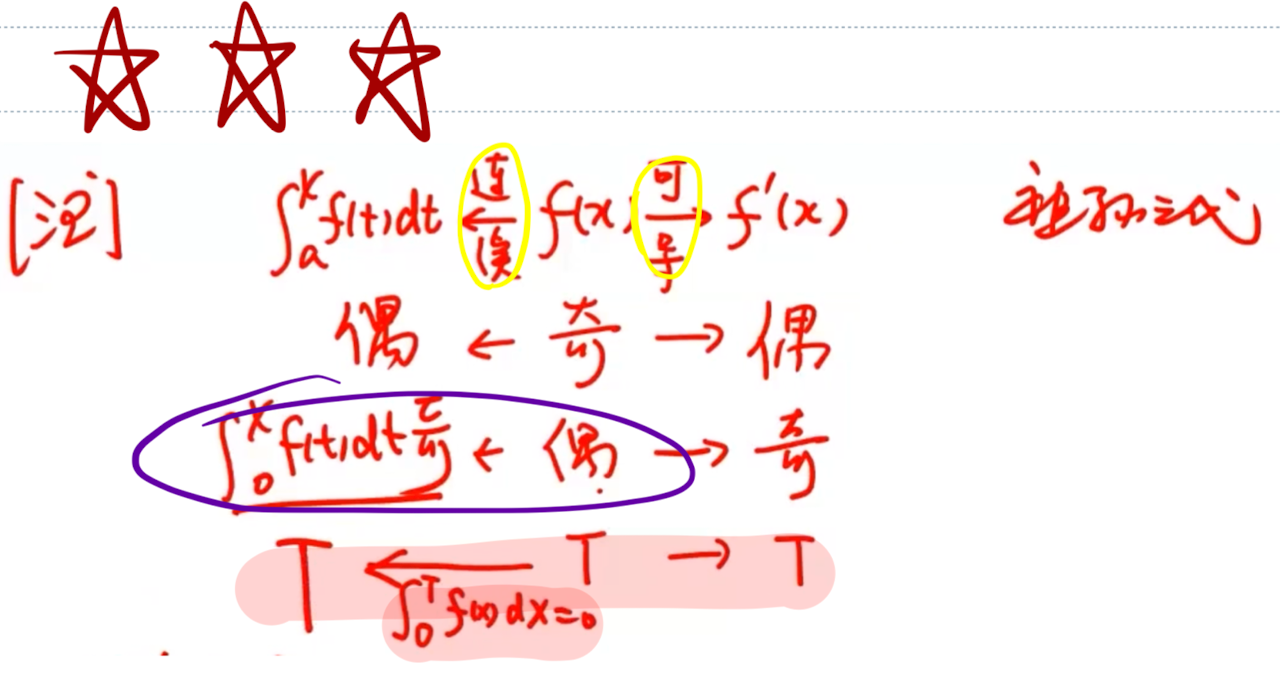
TIP

「不定积分」性质

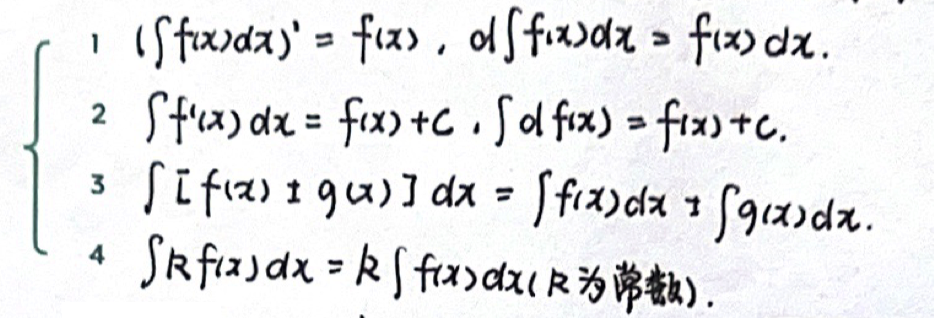
「不定积分」基本公式

「积分法」第一换元积分法（凑微分法）

• 本质是复合函数求导公式

「积分法」第二换元积分法（三种常用的变量代换）

「积分法」分部积分法（反对幂三指）

• 何时用
  • 两类不同函数相乘
  • ${\displaystyle \int udv=uv-\int vdu}$
• 如何用
  1. ${\displaystyle \int Pn(x)e^{\alpha x}dx}$ 、${\displaystyle \int Pn(x)sin\alpha xdx}$ 、${\displaystyle \int Pn(x)cos\alpha xdx}$ 多项式以外进微分
  2. ${\displaystyle \int e^{\alpha x}sin\beta xdx}$、${\displaystyle \int e^{\alpha }xcos\beta xdx}$ 指数、三角均可进，指数进入更简单，二次解出
  3. ${\displaystyle \int Pn(x)lnxdx}$、${\displaystyle \int Pn(x)arctanxdx}$、${\displaystyle \int Pn(x)arctanxdx}$ 多项式进微分

「积分法」积不出的积分

• ${\displaystyle \int e^{x^2}dx}$、${\displaystyle \int \frac{sinx}{x}dx}$ 、${\displaystyle \int \frac{cosx}{x}}$ 二重积分、交换次序

「可积函数积分」有理函数积分

• ${\displaystyle \int R(x)dx}$

「可积函数积分」三角有理式积分

• ${\displaystyle \int R(sinx,cosx)dx}$

一般方法（万能代换）- 工作量大

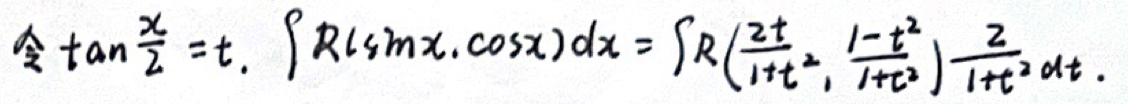
特殊方法（三角变形、换元、分部）

• ${\displaystyle \int R(sinx,cosx)dx}$
• 几种常见的换元法

「可积函数积分」简单无理函数积分

• ${\displaystyle \int R(x,\sqrt[n]{\frac{ax+b}{cx+d}})dx}$
• 一般法
• 根式代换
  • 
• 倒代换
  • 情况
    • 分母次数较高
  • 方法
    • ${\displaystyle x=\frac{1}{t}}$
• 整体代换
  • 情况
    • 出现复杂函数
  • 方法
    • 令 $\mathrm{复}\mathrm{杂}\mathrm{函}\mathrm{数}=t$

「不定积分」裂项 计算方法

分母为一次幂

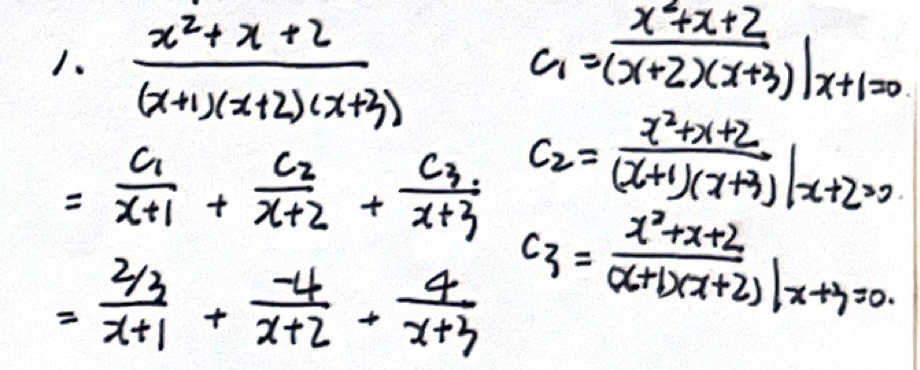
分母为高次幂

分母有一次多项式和高次多项式

分母有高次多项式与高次多项式相乘

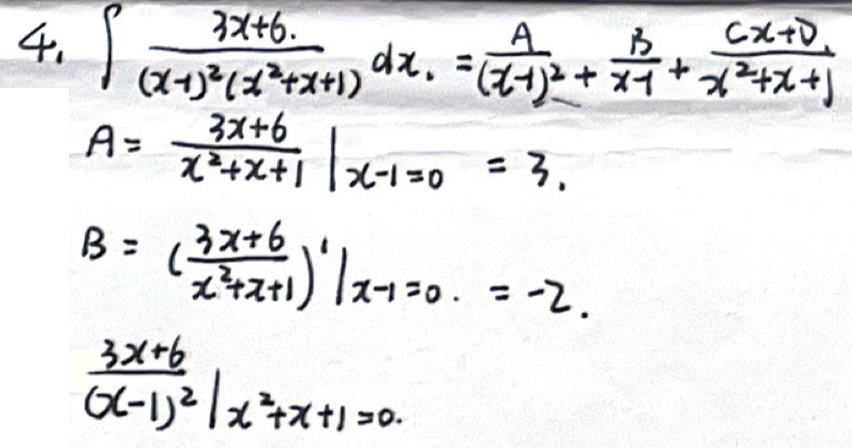
「不定积分」 凑微分法

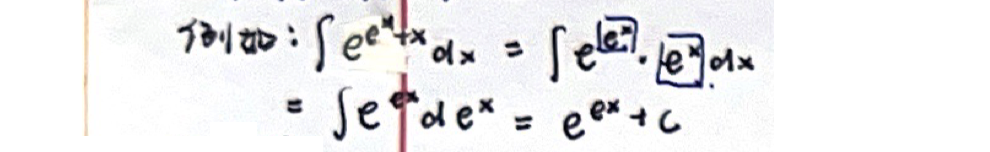
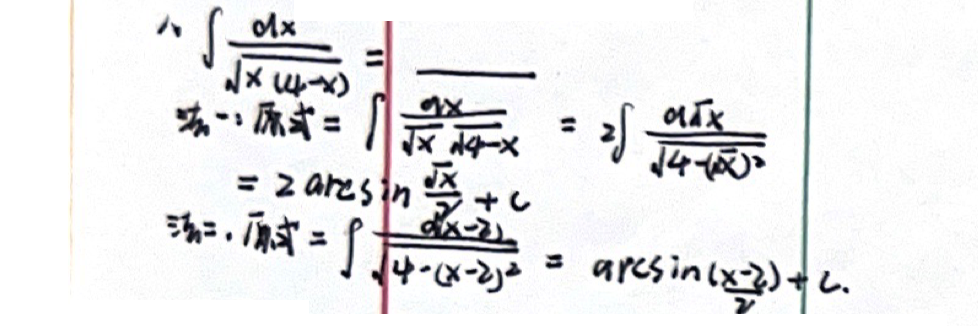
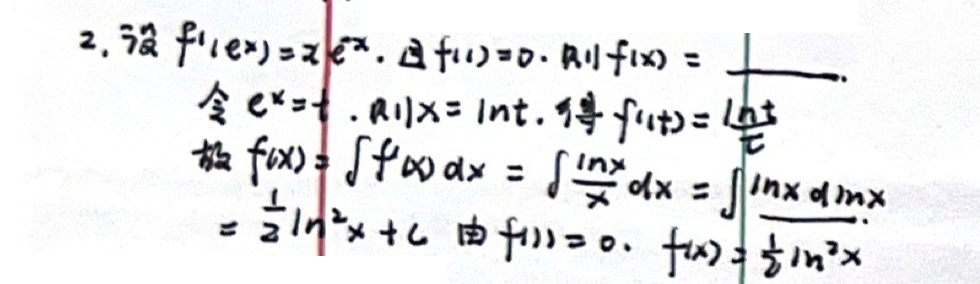
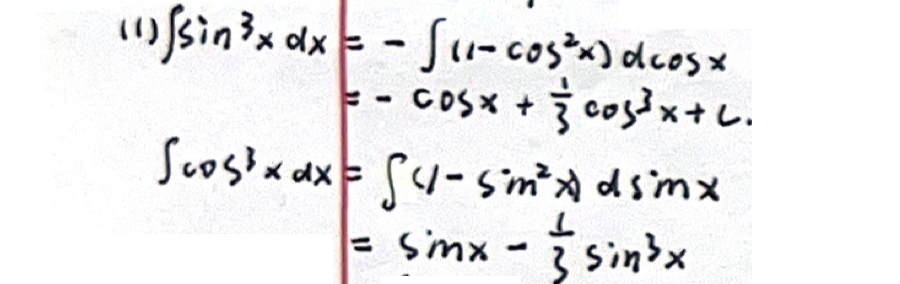
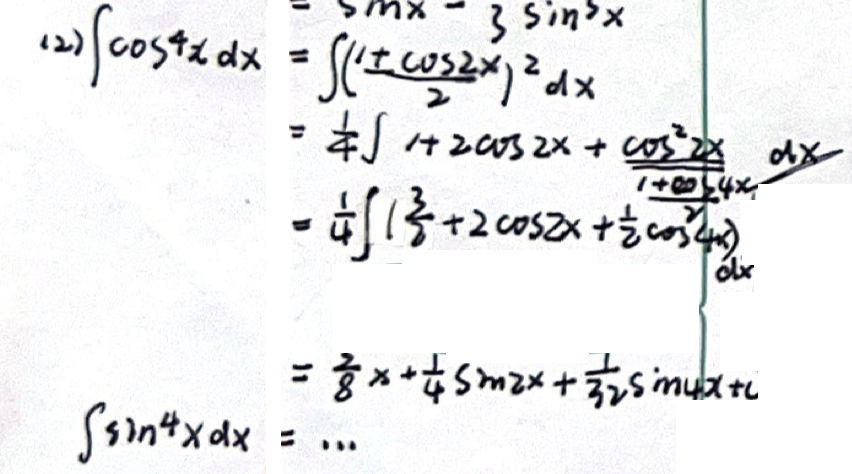
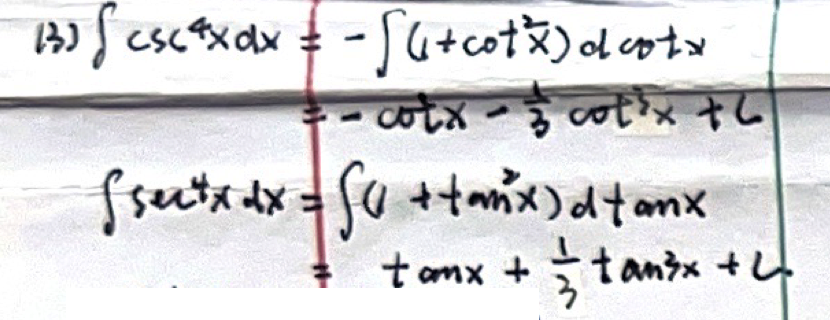
「不定积分」 分部积分法

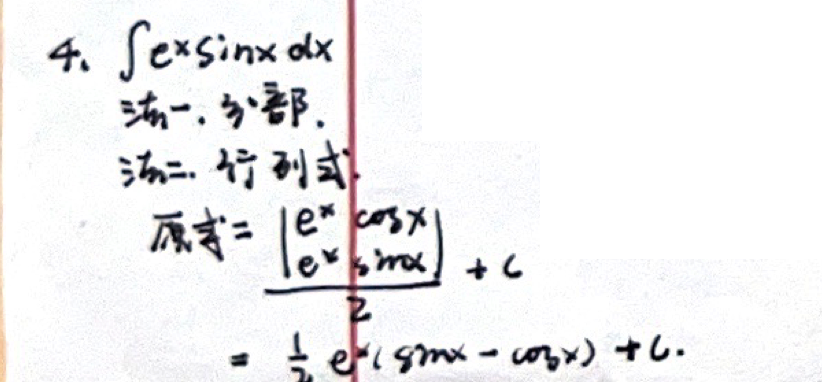
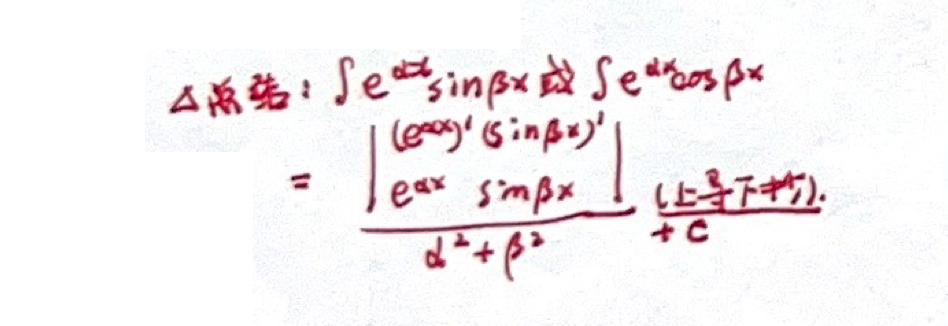
不定积分的积分法

凑微分法

换元法

恒等变形后、三角代换

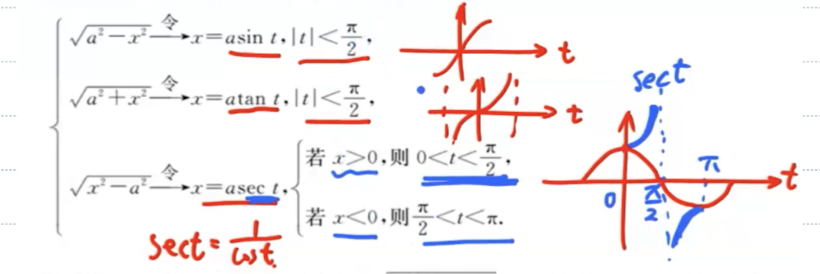
根式代换

倒代换

复杂函数的直接代换

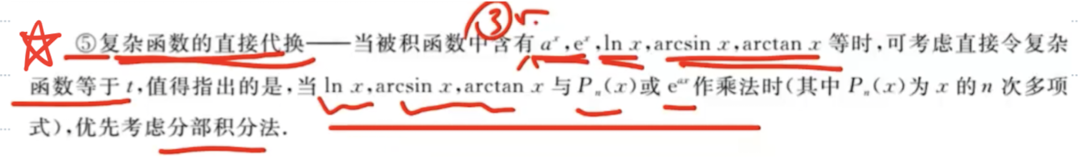
分部积分法

• 根据 反、对、幂、指、三 的原则

「题」分部积分法例题

分部积分法的推广

「⭐️」表格法求分部积分

有理函数的积分

取特殊值，快速计算系数