第一章 随机事件与概率

第一节 事件与概率的概念

• 事件：样本点的集合
• 概率：面积

「事件与概率」随机试验的定义

• 对随机现象进行观察称内随机试验，简称试验，记作 $E$。
• 它具有以下特点:
  1. 可以在相同条件下重复进行;
  2. 所有可能结果事前可知
  3. 试验之前不能确定哪个结果会发生

「事件」定义

事件		是什么	简记
随机事件		随机试验的结果	简称事件，记作 $A,B,C$
必然事件		每次试验必然发生的事件	称样本空间，记作 $\mathrm{\Omega }$
样本点		样本空间中的元素	基本事件，记作 $\omega$
不可能事件		每次试验不可能发生的事件	记作 $\mathrm{\Phi }$

样本点：实验中最小单位的结果

• 例如：
  • 抛骰子$\{1\},\cdots ,\{6\}$
  • $A=\{\mathrm{小}\mathrm{点}\}=\{1,2,3\}$
  • $\mathrm{\Omega }=\{1,\cdots ,6\}$

「事件」关系与运算

关系	关系式	解释
包含	$A\subset B$	若事件 $A$ 发生，事件 $B$ 一定发生，则称 $B$ 包含 $A$ 或 $A$ 包含于 $B$ ，记作 特别地，，记作
互相包含（相等）	$A=B$	若 $A\subset B$ 且 $B\subset A$，则称 $A$ 与 $B$ 相等
和	$A\cup B$	事件 $A$ 与 $B$ 至少有一个发生，称为 A 与 $B$ 的和
积	$AB$	事件 $A$ 与 $B$ 同时发生，称为 A 与 $B$ 的积
互不相容（互斥）	$AB=\mathrm{\varnothing }$	若事件 $A$ 与 $B$ 不能同时发生，称 $A$ 与 $B$ 互不相容
对立（互逆）	$B=\bar{A}$	若事件 $A$ 与 $B$ 不能同时发生，但必有一个发生，即 $A\cup B=\mathrm{\Omega }$ 且 $AB=\mathrm{\varnothing }$，则称 $A$ 与 $B$ 对立
差	$A-B$ $A-B=AB$	事件 $A$ 发生但事件 $B$ 不发生，称为 $A$ 与 $B$ 的差

「事件」运算律

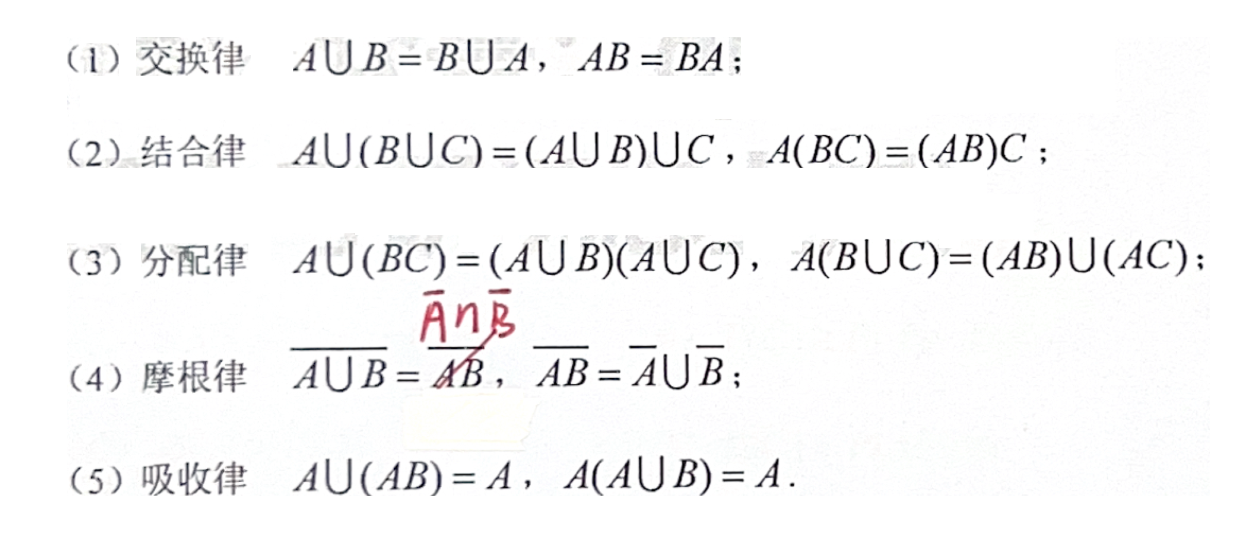
「概率」定义

「概率」性质

性质
有限可加性
单调不减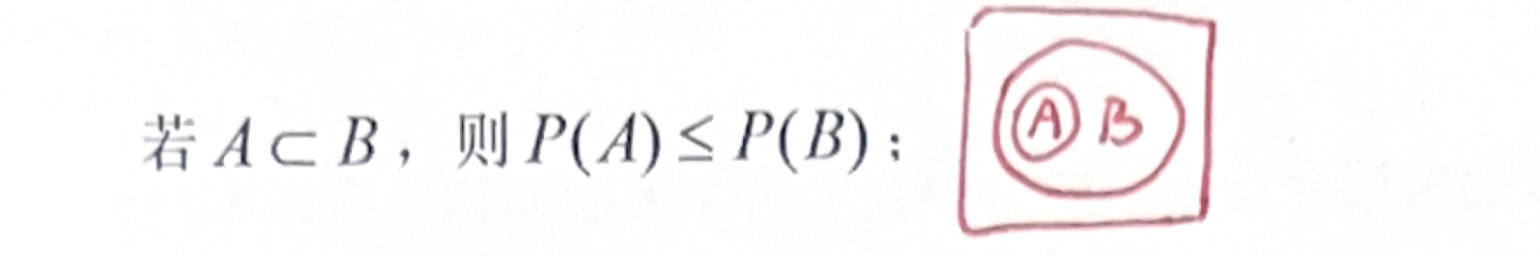
加法公式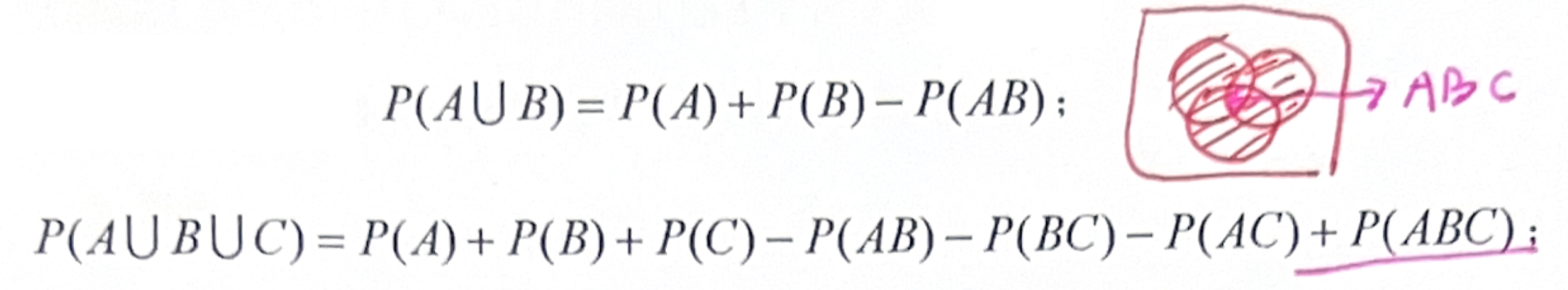
减法公式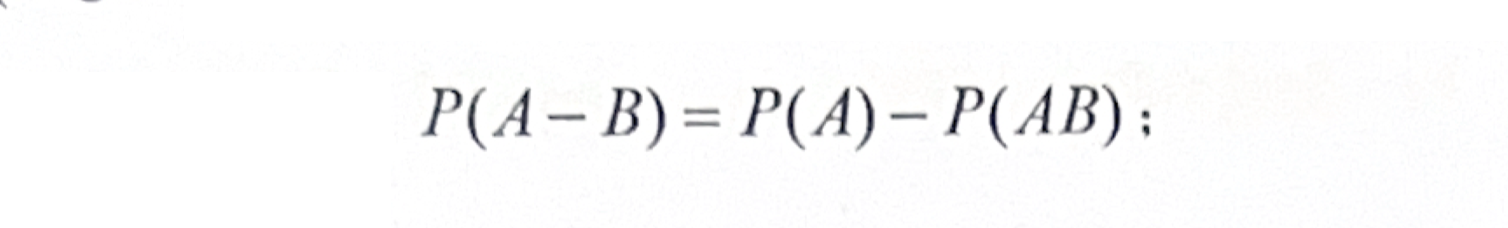
求逆公式

第二节 古典概型与几何概型

「回顾」加法原理与乘法原理

• 分类加法，分步乘法

「回顾」排列

「回顾」重复的排列（阶乘）

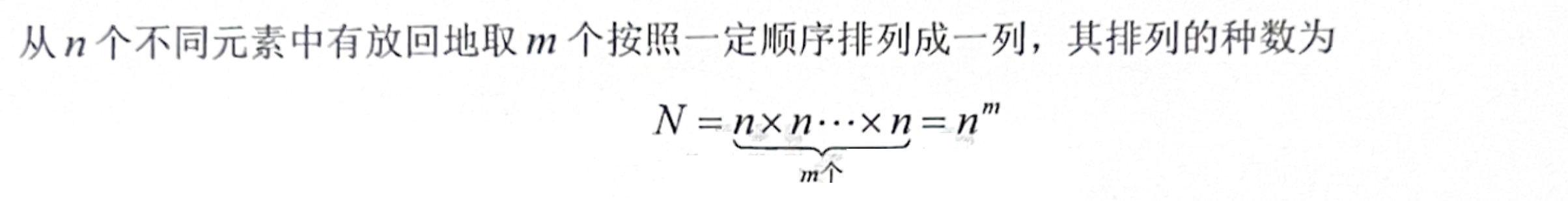
「回顾」组合

「古典概型」定义

• 设试验只有有限个等可能的样本点，称此实验为古典概型，事件 $A$ 的概率为

$$P(A)=\frac{A\mathrm{中}\mathrm{样}\mathrm{本}\mathrm{点}\mathrm{数}}{\mathrm{\Omega }\mathrm{中}\mathrm{样}\mathrm{本}\mathrm{点}\mathrm{数}}$$

• 在古典概型中，排列与组合概率相等

「几何概型」定义

• 设试验的样本空间为某区域，事件发生的可能性与其对应的几何度量成正比，称此试验为几何概型，事件 $A$ 的概率为

$$P(A)=\frac{A\mathrm{的}\mathrm{几}\mathrm{何}\mathrm{度}\mathrm{量}}{\mathrm{\Omega }\mathrm{的}\mathrm{几}\mathrm{何}\mathrm{度}\mathrm{量}}$$

「评注」

• 考试中对古典概型得考查通常结合离散型随机变量的概率分布,而几何概型则是均匀分布的试验背景.

第三讲 三大概率公式

「概率公式」条件概率公式（缩减样本空间）

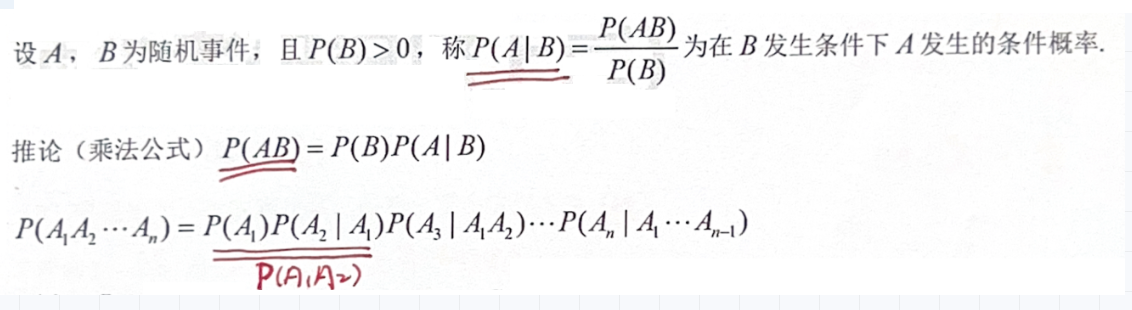
「概率公式」全概率公式（分割样本空间）

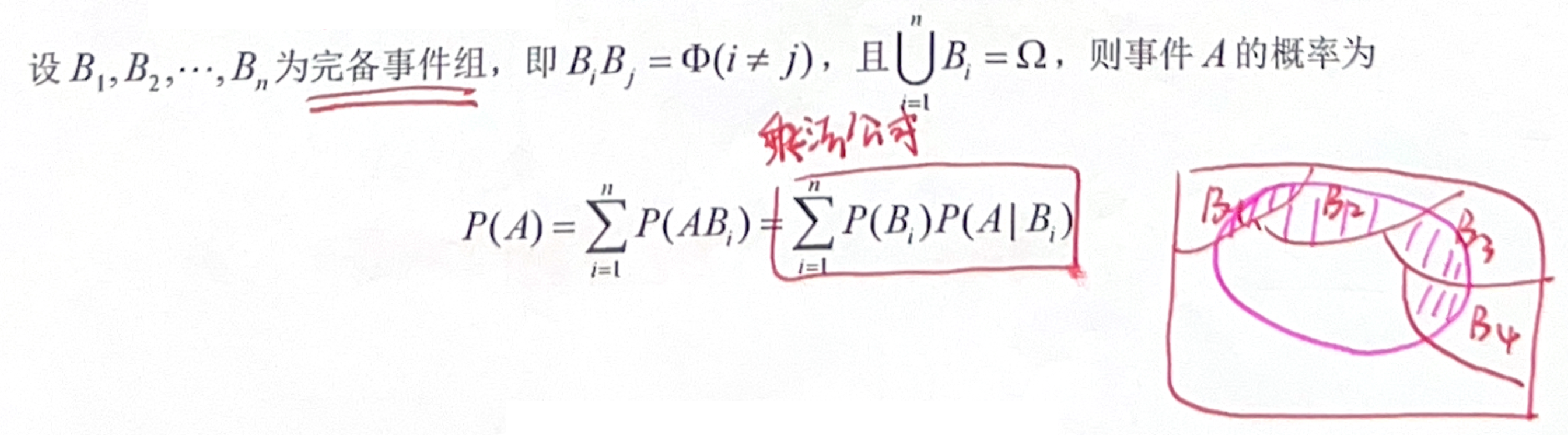
「概率公式」贝叶斯(Bayes)公式

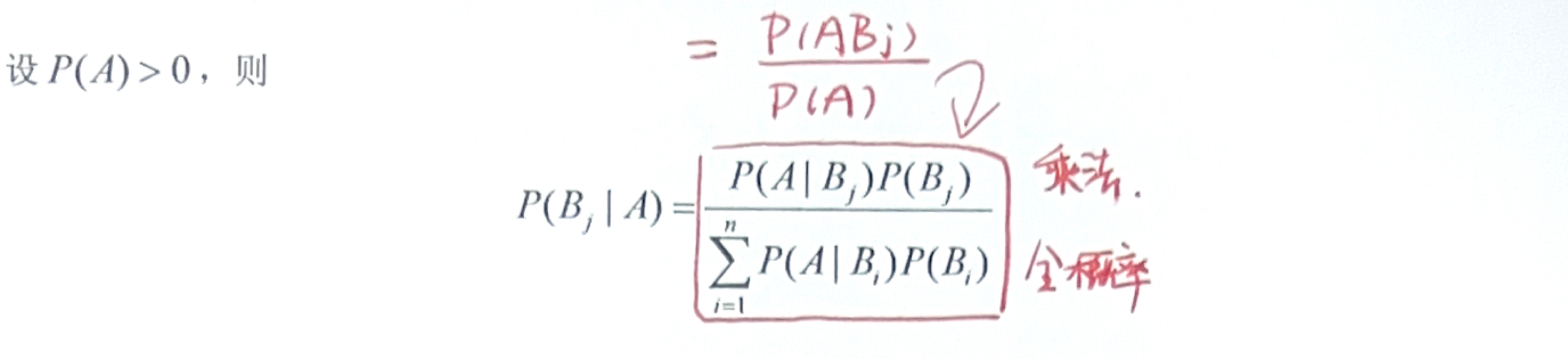
「评注」什么时候使用什么公式？

• 设试验分为两步，第一步有 $n$ 种情况($B_1,B_2,\cdots ,B_n$ 构成完备事件组)
• 若求第二步中事件 $A$ 的概率，则用全概率公式 $P(A)$
• 若已知事件 $A$ 发生，求在第一步哪种情况下发生的概率，则用贝叶斯公式 $P(B_j|A)$

第四节 事件独立性与伯努利概型

「事件相互独立」定义

• 设随机事件 $A,B$ 满足 $P(AB)=P(A)P(B)$，称 $A$ 与 $B$ 相互独立（互不影响）

「事件相互独立」充要条件

「评注」

1. 0 概率事件或 1 概率事件与任意事件相互独立，从而不可能事件或必然事件与任意事件相互独立
   1. $Pr:$ 设 $P(A)=0$，则$P(AB)=P(A)P(B)=0$
2. 若事件 $A$ 与 $B$ 既相互独立又互不相容，则 $A$ 与 $B$ 至少有一个为零概率事件
   1. 

「事件相互独立」n 个事件相互独立定义

相互独立与两两独立

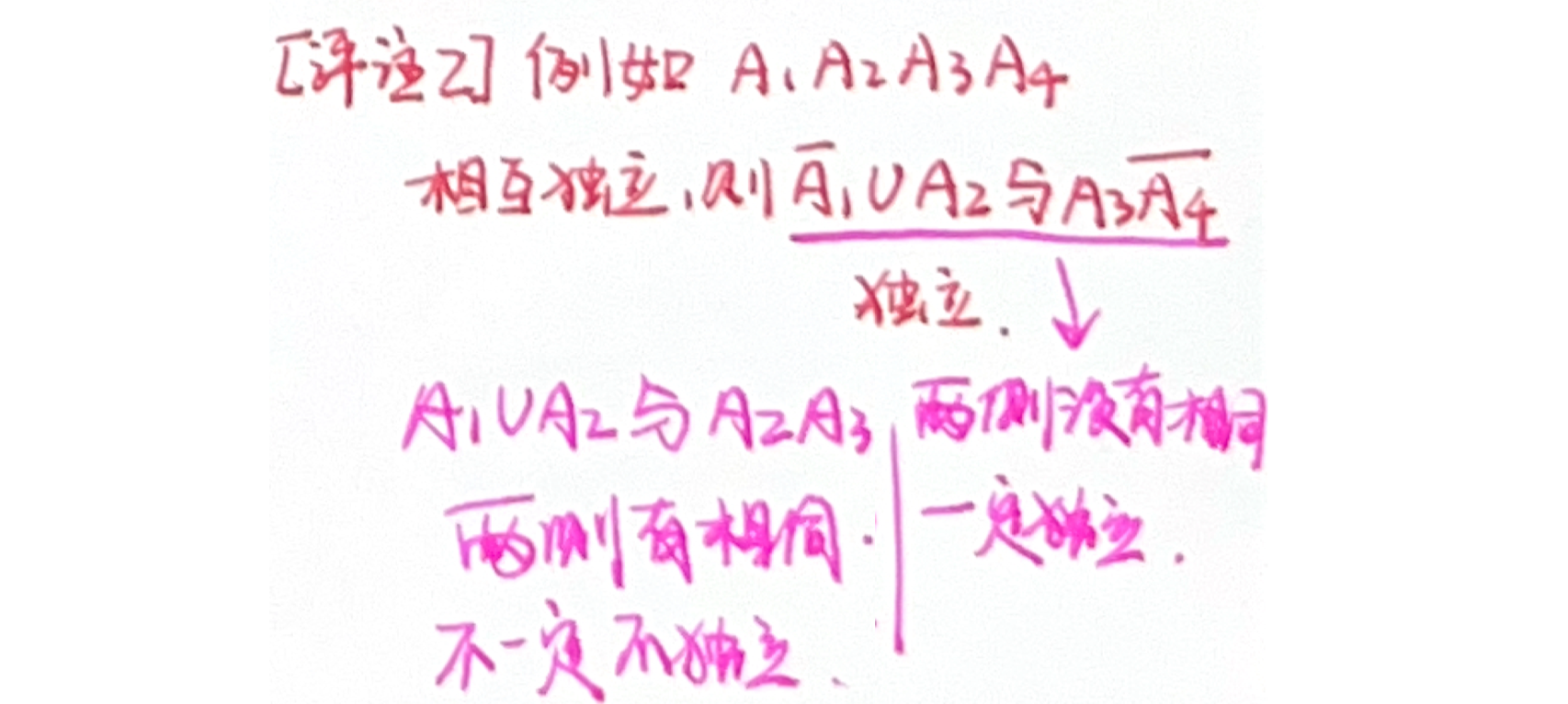
1. 事件 $A_1,A_2,\cdots ,A_n$ 相互独立一定两两独立，反之不成立。
2. 若 $A_1,A_2,\cdots ,A_n$ 相互独立，则由其中任意部分事件所产生的事件与另一部分事件所产生的事件相互独立。

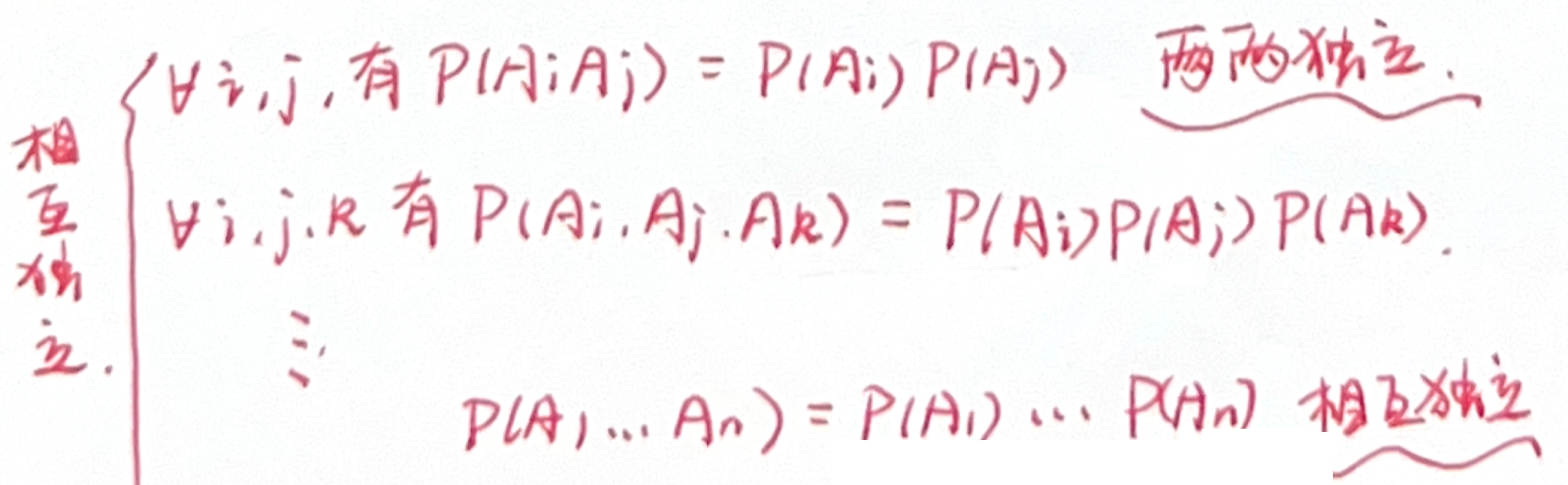
「伯努利概型」定义

• 设试验只有两个可能结果 $A$ 和 $\bar{A}$，称此试验为伯努利试验或伯努利概型。
• 将伯努利试验独立重复 $n$ 次，称为 $n$ 重伯努利试验
• 设 $p(A)=p(0<p<1)$，则 $n$ 重伯努利试验中 $A$ 发生 $k$ 次的概率为 $C_n^k{p}^k(1-p{)}^{n-k},k=0,1,\cdots ,n$