第十四节 多元函数基本概念

「多元函数极限」定义

• 平面点集 $D$，每个点 $P(x,y)\in D$，$z$ 按照法则 $f(x,y)$ 有一确定值对应，$z$ 为 $x,y$ 二元函数，记 $z=f(x,y)$，几何上表示空间曲面

「多元函数极限」存在的条件

• 极限要求 $(x,y)$ 在 $D$ 内以任意方式趋近于点 $(x_0,y_0)$，函数 $f(x,y)$ 都趋近于同一确定常数 $A$，否则极限不存在。

「多元函数极限」性质

• 一元函数极限性质在多元中仍然存在
  • 局部有界性
  • 保号性
  • 有理运算
  • 极限与无穷小的关系
  • 夹逼性

「多元函数连续性」连续的概念

「多元连续函数」性质

性质	解释
性质一	多元函数的和、差、积、商仍为连续函数
性质二	多元函数的复合函数也是连续函数
性质三	多元初等函数在其定义域内连续
性质四（最大值定理）	有界闭区域 D 上的连续函数在区域 D 上必能取得最大值和最小值
性质五（介值定理）	有界闭区域 D 上的连续函数在区域 D 上必能取得介于最大值和最小值之间的任何值

「偏导数」 定义

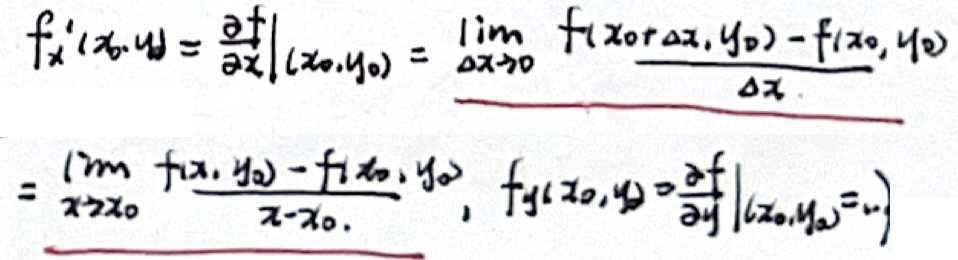
「高阶偏导数」定义

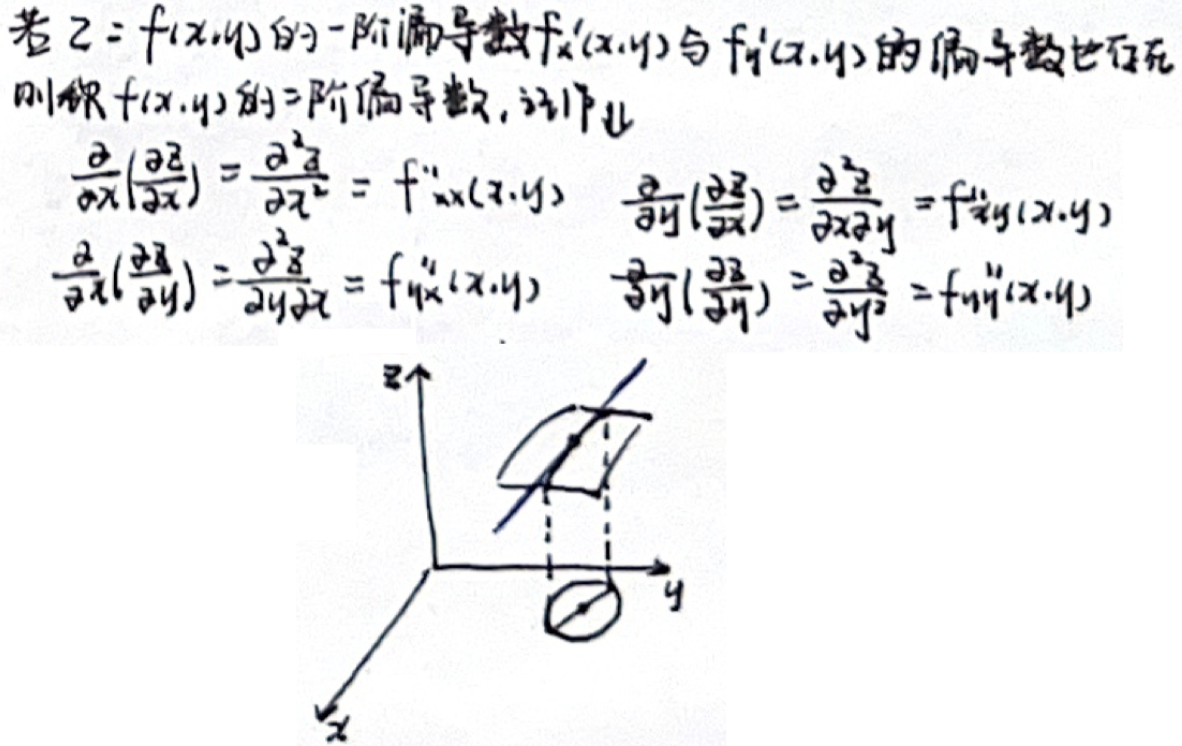
「高阶偏导数」定理

「全微分」定义

「可微」必要条件

「可微」定义判断可微（充要条件）

• $f_x^{\prime }(x,y)$ 和 $f_y^{\prime }(x,y)$ 是否均存在
• 若

$$\underset{\mathrm{\Delta }x\to 0\mathrm{\Delta }y\to 0}{lim}\frac{[f(x_0+\mathrm{\Delta }x,y_0+\mathrm{\Delta }y)-f(x_0,y_0)]-[f_x^{\prime }(x_0,y_0)\mathrm{\Delta }x+f_y^{\prime }(x_0,y_0)\mathrm{\Delta }y]}{\sqrt{(\mathrm{\Delta }x{)}^2+(\mathrm{\Delta }y{)}^2}}=0$$

• 则可微

「可微」充分条件

• 若 $f_x^{\prime }(x,y)$ 与 $f_y^{\prime }(x,y)$ 在 $(x_0,y_0)$ 连续，则 $f(x,y)$ 在点 $(x_0,y_0)$ 可微

「连续、可偏导及可微」之间的关系

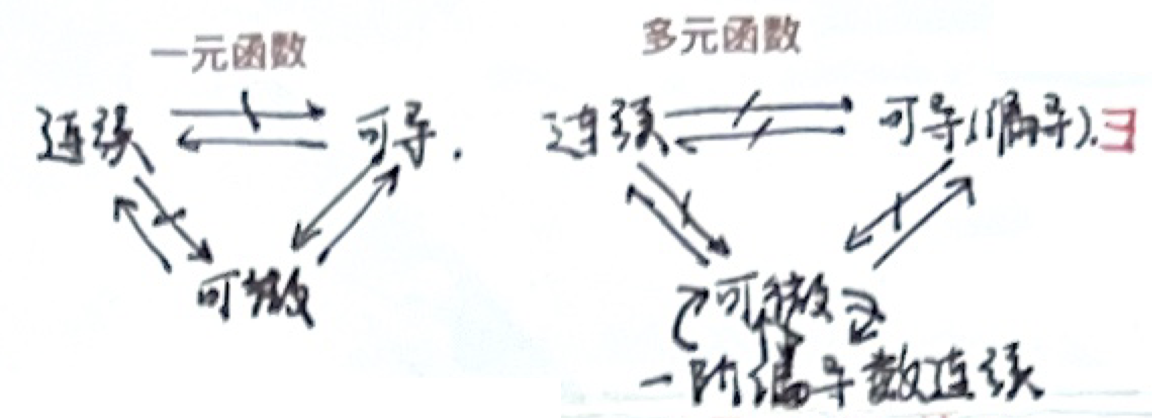
• 一阶偏导数连续，多元函数可微（证明超纲）
• 逆否命题成立
  • 一阶偏导数存在不一定可微，但是不存在一定不可微

「可微」充要条件