放在开始

我们首先准备两个字符串

• 文本串 ababababca
• 模式串 abababca

什么是暴力匹配？

通过两重循环，双指针，i指向文本串，j指向模式串，将指针所指向字符一一进行比对，匹配失败则i和j回到最开始的位置，i++，j = 0，重新进行比对，直到i到达文本串的长度减去模式串的长度，其时间复杂度 $O(m\times n)$​。

class Solution {
public:
    int strStr(string haystack, string needle) {
        int l1 = haystack.length();
        int l2 = needle.length();
        for(int i = 0; i < l1 - l2 + 1; i++){
            int j = 0;
            int k = i;
            while(haystack[k] == needle[j] && j < l2){
                if(j == l2 - 1) return i;
                j++;
                k++;
            }
        }
        return -1;
    }
};

什么是 KMP?

KMP算法相比于暴力匹配，可以使i指针在字符失配时，j 指针直接从最长公共后缀最后一个字符的下一个字符移动到最长公共前缀最后一个字符的下一个字符，而i指针不进行回退，减少时间复杂度，其时间复杂度为$O(m+n)$​。 首先我们要明确理解几个概念，知道什么是最长公共前后缀、什么是PMT。

什么是 最长公共前后缀？

当我们的文本串和模式串进行匹配时，当模式串匹配到第三个b的时候发生了失配

• 文本串 a b a b a c ...
• 模式串 a b a b a b ...

那么在失配字符前面存在前缀{ababa, abab, aba, ab, a} 那么在失配字符前面存在后缀{a, ba, aba, baba, ababa} 失配字符前子串{ababa}最长公共前后缀的前后缀字符长度不可与失配字符前子串长度相等，排除{ababa}，即最长公共前后缀为{aba}

什么是 PMT?

PMT为部分匹配表(Partial Match Table)，是字符串的前缀集合与后缀集合的交集中最长元素的长度。 如果待匹配的模式字符串有8个字符，那么PMT就会有8个值。

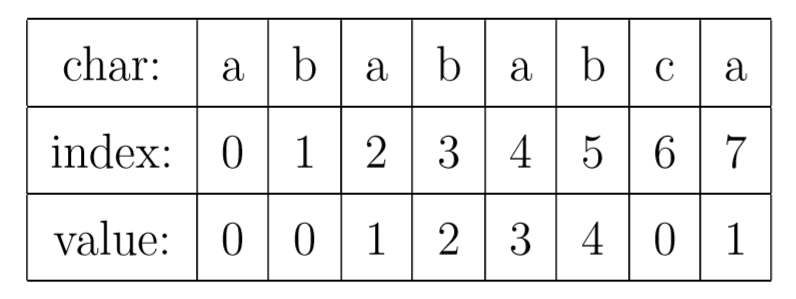
KMP过程

要在主字符串"ababababca"中查找模式字符串"abababca"。 如果在 j 处字符不匹配，那么由于前边所说的模式字符串 PMT 的性质，主字符串中 i 指针之前的 PMT[j−1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。 这是因为主字符串在 i 位失配，也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。 而我们上面也解释了，模式字符串从 0 到 j−1 ，在这个例子中就是”ababab”，其前缀集合与后缀集合的交集的最长元素为”abab”， 长度为4。 所以就可以断言，主字符串中i指针之前的 4 位一定与模式字符串的第 0 位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。 这样一来，我们就可以将这些字符段的比较省略掉。具体的做法是，保持i指针不动，然后将j指针指向模式字符串的PMT[j −1]位即可。

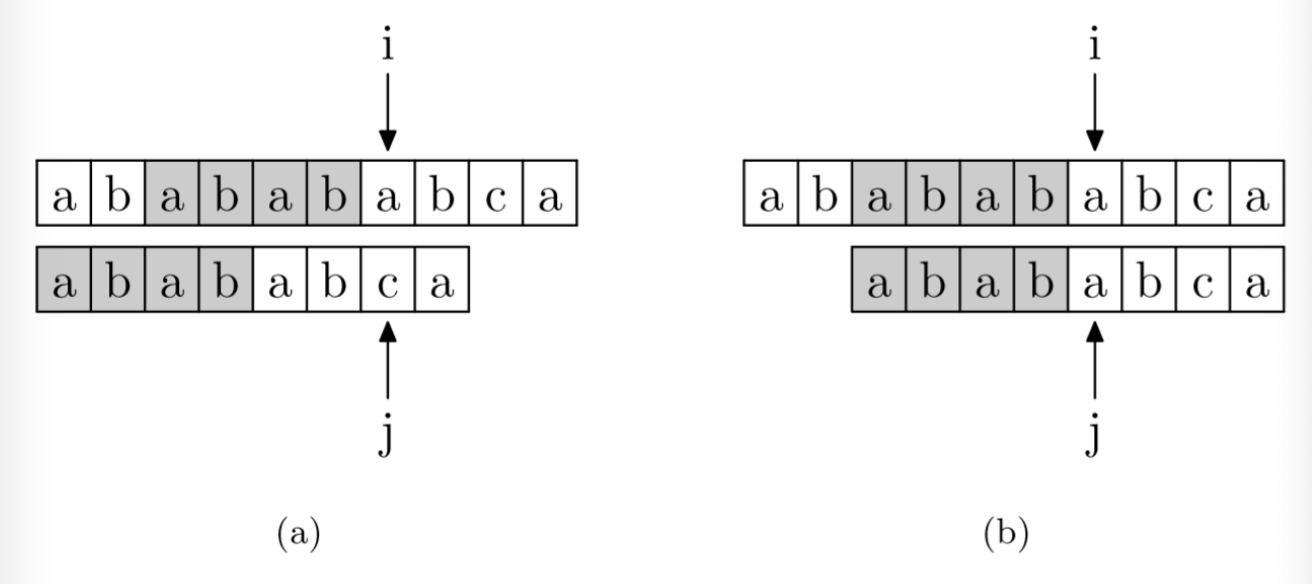
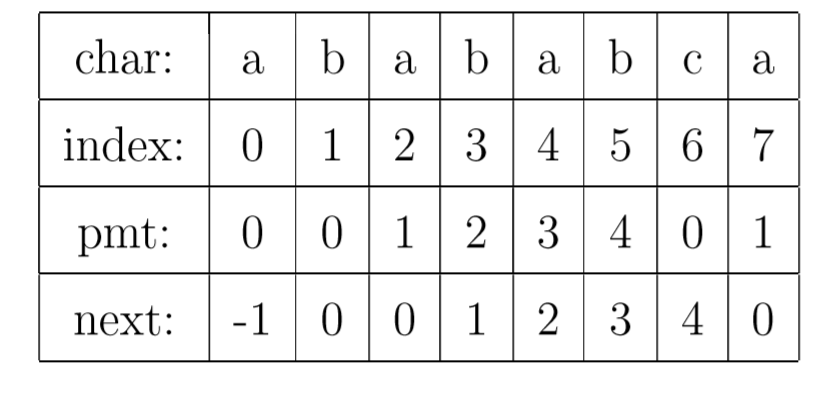
有了上面的思路，我们就可以使用PMT加速字符串的查找了。我们看到如果是在 j 位 失配，那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值，所以为了编程的方便， 我们不直接使用PMT数组，而是将PMT数组向后偏移一位。 我们把新得到的这个数组称为next数组。下面给出根据next数组进行字符串匹配加速的字符串匹配程序。 其中要注意的一个技巧是，在把PMT进行向右偏移时，第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。 在本节的例子中，next数组如下表所示。

int KMP(string haystack, string needle) { 
	int i = 0, j = 0;
	int *next = getNext(needle);
	while (i < haystack.length() && j < needle.length()) { 
		if (j == -1 || haystack[i] == needle[j]) { 
			i++; 
			j++; 
		} else 
			j = next[j]; 
	} 
	return j == needle.length() ? i - j : -1;
}

如何求得next数组

求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。

具体来说，就是从模式字符串的第一位(注意，不包括第0位)开始对自身进行匹配运算。 在任一位置，能匹配的最长长度就是当前位置的next值。如下图所示。

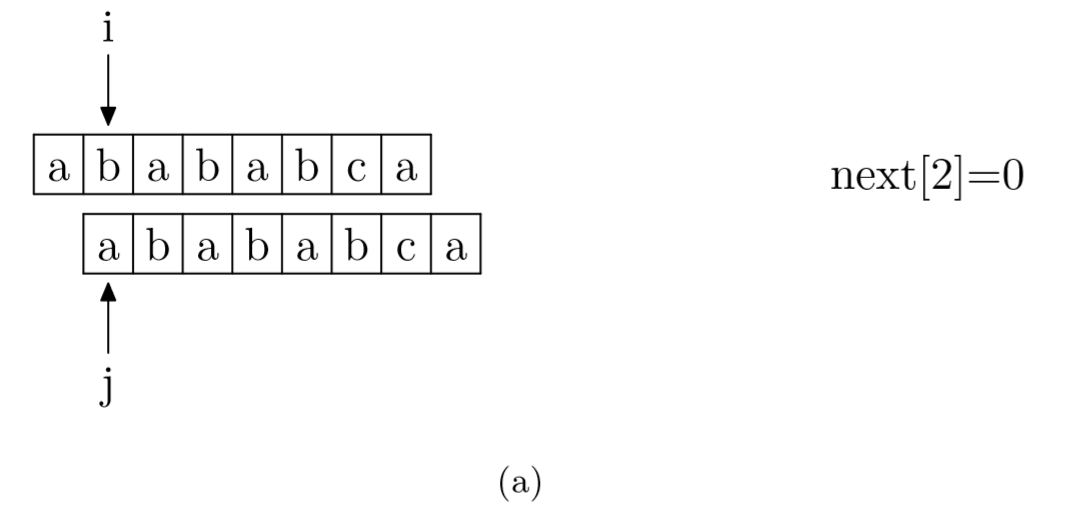
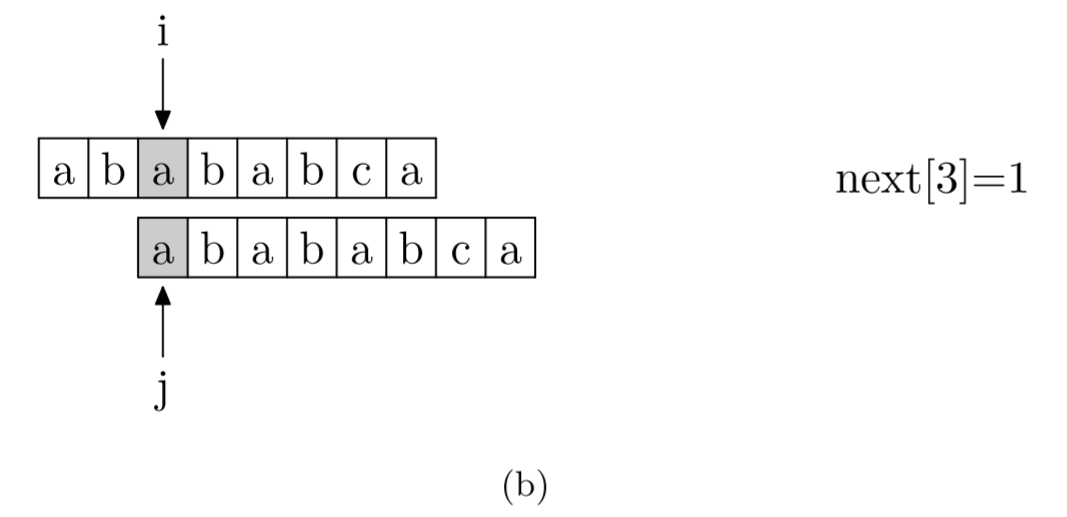
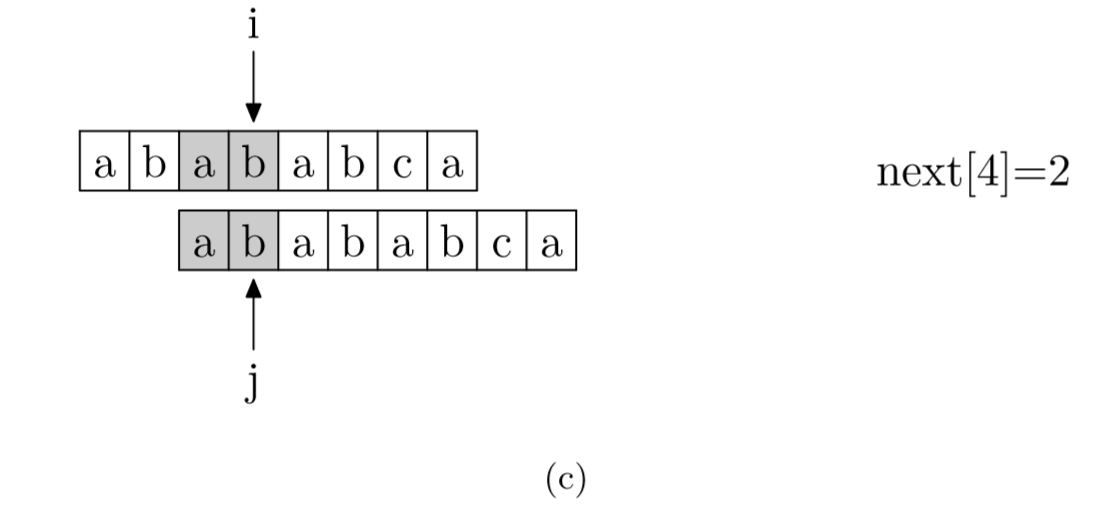
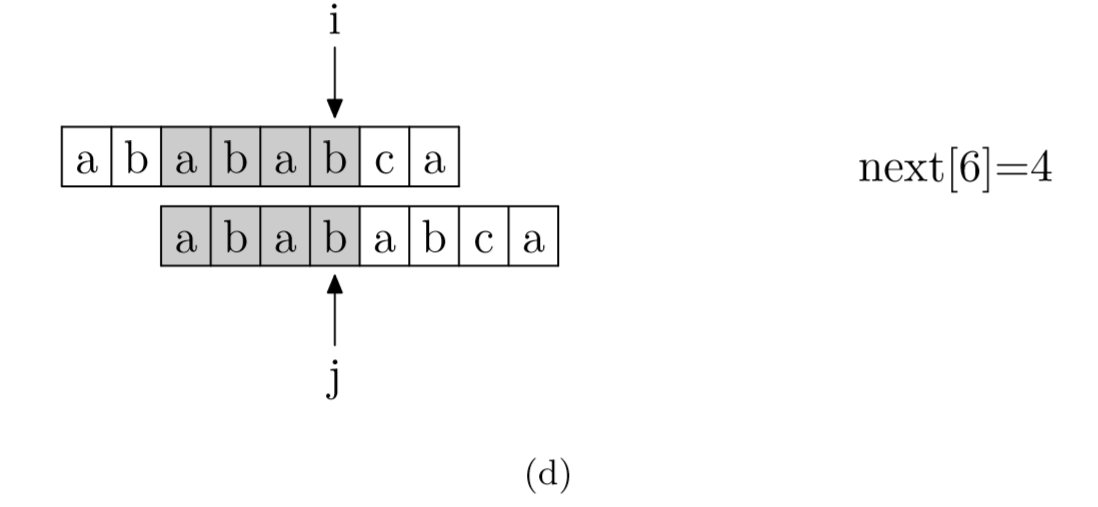
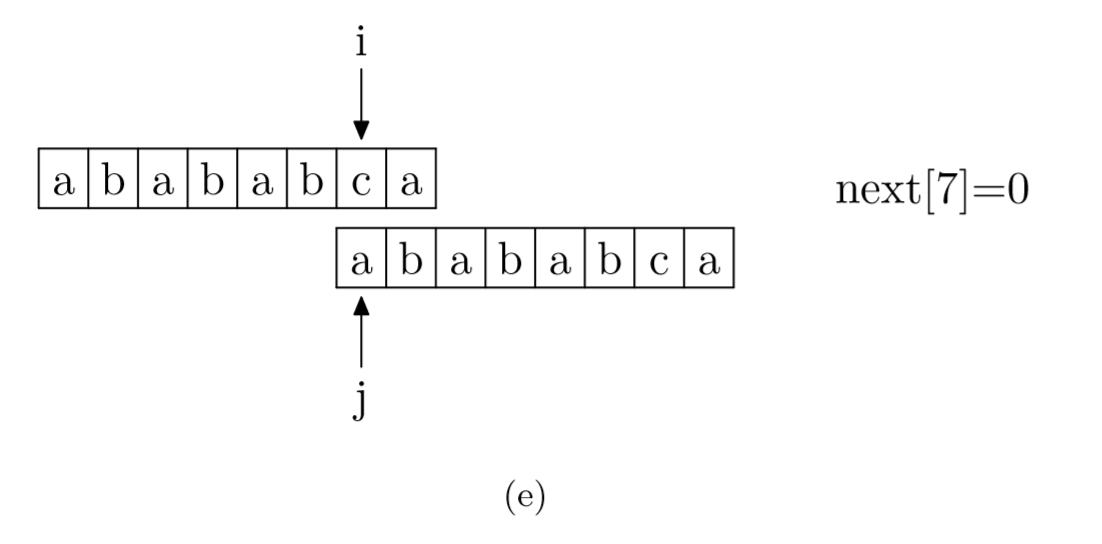
int* getNext(string needle){
        int l = needle.length();
        int* next = new int[l];
        next[0] = -1; // 初始化next数组的第一个值为-1
        int i = 0, j = -1;
        while(i < l - 1){ // i <= l
            if(j == -1 || needle[i] == needle[j]) next[++i] = ++j;
            else j = next[j];
        }
        return next;
    }

题目

28. 找出字符串中第一个匹配项的下标

引用

「知乎 海纳的回答」：https://www.zhihu.com/question/21923021/answer/281346746

「Bilibili KMP算法之求next数组代码讲解」：https://www.bilibili.com/video/BV16X4y137qw

「Bilibili KMP算法易懂版」：https://www.bilibili.com/video/BV1jb411V78H